Kezdőlap


Feladat:	1536. matematika feladat	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Farkas György , Tabiczky István , Takács László
Füzet:	1968/április, 147 - 149. oldal		PDF \| MathML
Témakör(ök):	Feuerbach-kör, Magasságpont, Diszkusszió, Háromszögek szerkesztése, Feladat
Hivatkozás(ok):	Feladatok: 1967/április: 1536. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen az $A B C$ háromszög magasságpontja $M$ . $B_{2}$ a $B C B_{2}$ és $M C B_{2}$ háromszögek közös derékszögének csúcsa, így rajta van a $B C$ és $M C$ átfogó fölé írt $k_{1}$ ill. $k_{2}$ Thalész-körön (1. ábra).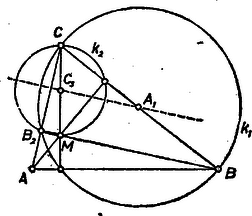

1. ábra

E két kör középpontja rendre az adott

A_{1}

, ill.

C_{3}

pont, így ismert

B_{2}

pontjuk alapján megrajzolhatók, és

B_{2}

-től különböző közös pontjuk

C

, ennek átellenes pontja

k_{1}

-ben

B

k_{2}

-ben

M

. Mivel

C A ⊥ B M

és

B A ⊥ C M

, a keresett háromszög hátra levő

A

csúcsa a már meghatározott

B C M

háromszög magasságpontja lesz.
Ha az adott

A_{1}

B_{2}

C_{3}

pontok különbözők,

k_{1}

és

k_{2}

mindig megrajzolhatók. Ahhoz azonban, hogy legyen

B_{2}

-től különböző közös pontjuk, az adott pontok nem eshetnek egy egyenesbe, hiszen különben

B_{2}

-ben érintenék egymást. Ha

C

és

B_{2}

különböző pontok, akkor egymás képei a körök

A_{1} C_{3}

centrálisára nézve, valódi háromszöget alkotnak

A_{1}

-gyel és

C_{3}

-mal, ezért valódi háromszög lesz

C A_{1} C_{3}

-nak

C

-ből kétszeresére nagyított képe, a

C B M

háromszög is. A

C B M

háromszög

A

magasságpontja nem azonos a

B

C

csúcsokkal, ha sem a

C B M ∢

, sem a

B C M ∢

nem derékszög. Ebben az esetben

A C ⊥ B M

A B ⊥ C M

miatt

M

magasságpontja az

A B C

háromszögnek és

A_{1}

C_{3}

valóban a

C B

C M

szakaszok felezőpontja. Mivel az

M B C ∢

nem derékszög,

C

-t az

A_{1}

-re, valamint az

A_{1} C_{3}

egyenesre tükrözve különböző pontokba jutunk, tehát

B_{2}

nem azonos

B

-vel, sem

C

-vel, így

B_{2}

-ből az

A C

szakasz

90^{\circ}

alatt látszik,

B_{2}

tehát valóban az

A B C

háromszög

B

csúcsához tartozó magasságának a talppontja. Ezek szerint az

A B C

háromszög eleget tesz a követelményeknek.

II. Vizsgáljuk meg azokat az eseteket, amikor a szerkesztés nem végezhető el. Ha az

A_{1}

B_{2}

C_{3}

pontok különbözők, de egy egyenesbe esnek, akkor

C

azonosnak adódik

B_{2}

-vel, tehát a keresett

A B C

háromszögnek

C

-nél

90^{\circ}

-os szöge volna, hiszen

C A ⊥ B M ∥ A_{1} C_{3}

miatt mindig

C A ⊥ A_{1} C_{3}

. Ámde ekkor az

M

magasságpont és az

M C

szakasz

C_{3}

felezőpontja is azonos volna

C

-vel, tehát

B_{2}

és

C_{3}

nem lehetne különböző, ami ellentmondás. Ebben az esetben tehát nincs megoldása a feladatnak.
Ha az

A_{1}

B_{2}

C_{3}

pontok nem esnek egy egyenesbe, akkor a szerkeszthetőség feltétele ‐ mint láttuk ‐ az, hogy a

B C M

háromszögben se a

B

, se a

C

csúcsban ne adódjék derékszög. Mivel a

B C M

háromszöget úgy kapjuk, hogy az

A_{1} B_{2} C_{3}

háromszöget az

A_{1} C_{3}

oldalra tükrözzük, majd az így kapott

A_{1} C C_{3}

háromszöget a

C

csúcsból kétszeresére nagyítjuk, a szerkeszthetőség feltétele az, hogy az

A_{1}

B_{2}

C_{3}

pontok által meghatározott (valódi) háromszögben se az

A_{1}

, se a

B_{2}

csúcsnál ne legyen derékszög.
Tekintsük még azokat az eseteket, amikor az adott pontok közül kettő azonos. Mivel a

B C

oldal

A_{1}

felezőpontja nem lehet az

A C

oldal egyenesén,

A_{1}

és

B_{2}

nem lehet azonos.

B_{2}

és

C_{3}

csak úgy lehet azonos, ha

M

és

C

is azonos velük, vagyis az

A B C

háromszögben

C

-nél derékszög van. Ekkor viszont az adatok csak a

B C

oldalt határozzák meg, az

A

csúcs a

B C

-re a

C

pontban emelt merőleges tetszőleges pontja lehet. Ha végül

A_{1}

és

C_{3}

azonos, akkor

M

azonos

B

-vel, és a feladatnak ismét végtelen sok megoldása van.
Tabiczky István (Győr, Révai M. gimn. III. o. t.)
Takács László (Sopron, Széchenyi I. gimn. III. o. t.)

II. megoldás (vázlat). Az adott pontok mindegyike rajta van a keresett háromszög

k_{9}

Feuerbach-féle körén, ennélfogva

k_{9}

megszerkeszthető, legyen a középpontja

F

. És mivel egy oldalszakasz felezőpontja és a rá merőleges magasságvonalon a csúcs és magasságpont közti szakasz felezőpontja

k_{9}

egy átmérőjének végpontjait adják, azért

C_{3}

-nak

F

-re vett tükörképe

C_{1}

, az

A B

oldal felezőpontja. Ekkor az

A_{1} C_{1}

egyenes megadja az

A C

oldal irányát, ezért a

B_{2}

-n átmenő,

A_{1} C_{1}

-gyel párhuzamos egyenes

k_{9}

-ből kimetszi

B_{1}

-et, az

A C

oldal felezőpontját, ekkor pedig hasonlóan az

A B

oldalegyenes átmegy

C_{1}

-en és párhuzamos

A_{1} B_{1}

-gyel,

B C

pedig átmegy

A_{1}

-en és párhuzamos

B_{1} C_{1}

-gyel.
Ekkor a

k_{9}

kör, mint az

A_{1}

B_{1}

C_{1}

pontokon átmenő kör, a szerkesztett háromszög Feuerbach-köre, ennek az

A C

oldallal való másik metszéspontja

B_{2}

, a magasság talppontja,

C_{1}

-gyel átellenes

C_{3}

pontja pedig

C M

felezőpontja, tehát az

A B C

háromszög megfelel a követelményeknek (2. ábra).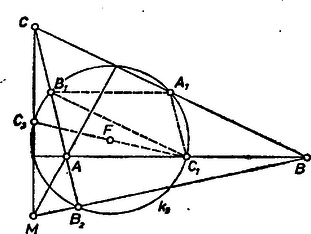

2. ábra

Farkas György (Budapest, Landler J. techn. II. o. t.)