Feladat:	1535. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Andor Cs. ,  Bajmóczy E. ,  Balogh J. ,  Bán Ilona ,  Berács J. ,  Bodor I. ,  Draschitz R. ,  Fuggerth E. ,  Gegesy F. ,  Hunyadvári L. ,  Juhász Ágnes ,  Kas P. ,  Katz Sándor ,  Kóczy L. ,  Lakatos L. ,  Losonci Z. ,  Mérő László ,  Mészáros J. ,  Moson P. ,  Munk S. ,  Nagy L. ,  Nagy Zs. ,  Orbán G. ,  Péli Katalin ,  Perémy G. ,  Pintér Ágnes ,  Printz J. ,  Somos E. ,  Szabó Klára ,  Takács L. ,  Tátray P. ,  Turchányi Piroska ,  Varsányi Anikó ,  Zöldy B.
Füzet:	1968/március, 102 - 105. oldal		PDF  |  MathML
Témakör(ök):	Eltolás, Terület, felszín, Egyéb sokszögek geometriája, Szögfüggvények, síkgeometriai számítások, Szabályos sokszögek geometriája, Feladat
Hivatkozás(ok):	Feladatok: 1967/április: 1535. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. $\begin{array}{c}{\displaystyle t=5\text{sin}\alpha +4\text{sin}2\alpha +3\text{sin}3\alpha +2\text{sin}4\alpha +\text{sin}5\alpha \mathrm{.}}\end{array}$ (1) I. Megmutatjuk, hogy a vizsgálandó $T$ tizenkétszög szimmetrikus a két kivételes csúcsot, $A$-t és $B$-t összekötő átlójára. $A$ és $B$ két törött vonalra bontja $T$ kerületét. Forgassuk el az egyiket $A$ körül úgy, hogy a két törött vonal $A$-ban csatlakozó szakaszai közti szög is egyenlő legyen a szabályos $16$-szög szögével, és legyen az elfordított törött vonal szabad végpontja 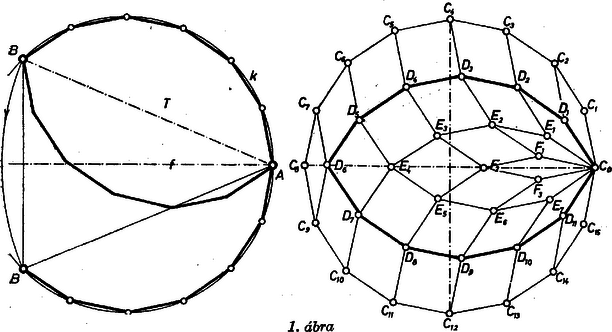$B\text{'}$.     Ekkor a $BAB\text{'}$ törött vonal úgy származtatható egy egységnyi oldalú $S$ szabályos $16$-szög kerületéből, hogy annak $4$ egymás utáni oldalát a $BB\text{'}$ átlóval levágjuk. A forgatás miatt $B\text{'}A=BA$, ezért $A$ rajta van a $BB\text{'}$ átló $f$ felező merőlegesén. $BB\text{'}$ az $S$ köré írt $k$ körnek húrja, ezért $f$ a $k$-nak átmérője, és $S$-nek szimmetriatengelye, így az $AB$, $AB\text{'}$ törött vonalak egymás képei $f$-re, tehát mindkét törött vonal ugyanannyi, azaz $6$ oldalt tartalmaz $T$ kerületéből. (Az 1. ábra alsó $B$ pontja helyesen $B\text{'}$.) II. Legyenek egy egységnyi oldalú $S$ szabályos $16$-szög egymás utáni csúcsai $C_0$, $C_1$, $\cdots$, $C_{15}$ (az előbbi jelölésekkel pl. $C_0=A$, $C_6=B$, $C_{10}=B\text{'}$). Toljuk el a $C_1{C}_2\text{...}{C}_7$ törött vonalat a $\overrightarrow{C_1{C}_0}$ vektorral a $C_0{D}_1\text{...}{D}_6$ helyzetbe. Így $D_6$ az $S$-nek $C_0{C}_8$ tengelyén adódik, mert $C_0{D}_6\parallel C_1{C}_7\parallel C_0{C}_8$, hiszen $C_0{C}_1{C}_7{D}_6$ paralelogramma, másrészt mert a $C_0$ és $C_8$, valamint a $C_1$ és $C_7$ csúcsok egymás képei a $C_4{C}_{12}$ tengelyre. A $C_{15}{C}_{14}\text{...}{C}_9$ törött vonalat a $\overrightarrow{C_{15}{C}_0}$ vektorral eltolva $C_9$ ugyancsak $D_6$-ba jut, hiszen új helyzete $C_{15}{C}_0\#C_8{C}_7$ miatt paralelogrammát alkot a $C_7$, $C_8$, $C_9$ csúcsokkal, másrészt $C_9{C}_8{C}_7{D}_6$ ugyancsak paralelogramma, mert $C_8{C}_9\#C_1{C}_0$ $\#C_7{D}_6$. A $C_1{C}_2\text{...}{C}_7$ és a $C_{15}{C}_{14}\text{...}{C}_9$ törött vonal egymás tükrös párja a $C_0{C}_8$ tengelyre, másrészt kezdőpontjukat e tengely ugyanazon pontjába toltuk, ezért az eltolás utáni helyzetek is tükrösek $C_0{C}_8$-ra. Így $C_{10}$, $\text{...}$, $C_{14}$ új helyzetét $D_7$-tel, $\text{...}$, $D_{11}$-gyel jelölve a $C_0{D}_1\text{...}{D}_6\text{...}{D}_{11}=T_{12}$ tizenkétszögnek egyrészt megvannak a feladatban előírt tulajdonságai, másrészt teljesül rá ezeknek az I. részben bebizonyított következménye: a szabályos $16$-szög szögeitől különböző szögeinek csúcsa $C_0$ és $D_6$, és kerületének e két csúcs közötti részei $6-6$ oldalból állnak. Ezért az állítást $T_{12}$-re kell bebizonyítanunk. Legyen a $D_1{D}_2{D}_3{D}_4{D}_5$ és $D_{11}{D}_{10}{D}_9{D}_8{D}_7$ törött vonalnak a $\overrightarrow{D_1{C}_0}$, ill. $\overrightarrow{D_{11}{C}_0}$ vektorral való eltolás utáni helyzete $C_0{E}_1{E}_2{E}_3{E}_4$, ill. $C_0{E}_7{E}_6{E}_5{E}_4$, az $E_1{E}_2{E}_3$ és $E_7{E}_6{E}_5$ törött vonalnak az $\overrightarrow{E_1{C}_0}$, ill. $\overrightarrow{E_7{C}_0}$ vektorral való eltolás utáni helyzete $C_0{F}_1{F}_2$, ill. $C_0{F}_3{F}_2$ (a fentiekhez hasonlóan $E_4$, ill. $F_2$ ismét közös végpontok a $C_0{C}_8$ tengelyen, és az új helyzetek is páronként tükrösek a tengelyre). A csúcsoknak az eltolásokban megtett útját is berajzolva $S$-et és benne $T_{12}$-t felosztottuk egységnyi oldalú rombuszokra, $T_{12}$-ben $15$ rombusz keletkezett. A rombuszok tompaszöge a $D_1$, $E_1$, $F_1$ pontnál (és tükörképükben is, a következőket is így értve) $S$ szögével egyenlő, ami egyszerű számítás szerint $7\alpha$, a $C_2$, $D_2$, $E_2$ pontnál $6\alpha$, a $C_3$, $D_3$, $E_3$ pontoknál, valamint $D_6$-nál $5\alpha$, $D_4$-nél $4\alpha$ (derékszög), ennélfogva a hegyesszögek nagysága rendre $\alpha$, $2\alpha$, ill. $3\alpha$. Így a rombuszok magassága rendre $\text{sin}\alpha$, $\text{sin}2\alpha$, $\text{sin}3\alpha$, ill. $\text{sin}4\alpha =1$, és az egységnyi alapok miatt ennyi a területek mértékszáma is. Mármost $T_{12}$-ben az $\alpha$ hegyes szöggel bíró rombuszok száma $5$, a $2\alpha$, ill. $3\alpha$ hegyesszöggel bíróké $4-4$, végül a négyzeteké $2$. Ezek alapján ‐ és figyelembe véve, hogy $\text{sin}3\alpha =\text{sin}5\alpha$ ‐ a $15$ rombusz területének összegére (1)-et kapjuk.     Katz Sándor (Paks, Vak Bottyán gimn. III. o. t.)   Mérő László (Budapest, Berzsenyi D. g. III. o. t.)   Megjegyzések. 1. Az $S$ idomot rombuszokra osztó hálózatot a $C_0{C}_1\text{...}{C}_7$ és $C_0{C}_{15}\text{...}{C}_9$ törött vonalak $C_0$ körüli egymás utáni $\alpha$, $2\alpha$, $\text{...}$, $6\alpha$ szöggel való elfordításával is megkaphatjuk. 2. Megoldásunkból az is adódik, hogy $S$ területe így is írható: $\begin{array}{c}{\displaystyle t_{16}=7\text{sin}\alpha +6\text{sin}2\alpha +\text{...}+2\text{sin}6\alpha +\text{sin}7\alpha \mathrm{.}}\end{array}$ Hasonlóan az $a=1$ oldalú szabályos $2n$-szög területe, $\alpha =2\pi /n$ jelöléssel 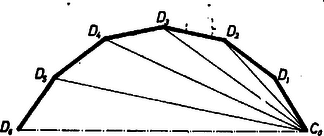$\begin{array}{c}{\displaystyle t_{2n}=\left(n-1\right)\text{sin}\alpha +\left(n-2\right)\text{sin}2\alpha +\text{...}+2\text{sin}\left(n-2\right)\alpha +\text{sin}\left(n-1\right)\alpha \mathrm{.}}\end{array}$ 3. Felhasználva a fenti I. rész megállapítását ($T$-nek $C_0{D}_6$ egyik oldalán levő felét a $C_0$-bó1 kifutó átlókkal háromszögekre bontva az egymás utáni átlók közti szög mindig $\alpha /2$, az egymás utáni átlók a végpontjukba befutó, $C_0$-hoz közelebbi oldallal $\alpha /2$-nek rendre az $1$-, $2$-, $3$-, $4$-, $5$-szörösét zárják be, a továbbmenő oldallal pedig a $13$-, $12$-, $11$-, ill. $10$-szeresét.     2. ábra   Így a háromszög $\left(c^2\text{sin}\alpha \text{sin}\beta \right)/\left(2\text{sin}\gamma \right)$ területképlete alapján ${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{t}{2}=\frac{1}{2\text{sin}\frac{\alpha }{2}}\left(\text{sin}\frac{\alpha }{2}\text{sin}\frac{14\alpha }{2}+\text{sin}\frac{2\alpha }{2}\text{sin}\frac{13\alpha }{2}+\text{sin}\frac{3\alpha }{2}\text{sin}\frac{12\alpha }{2}+\text{sin}\frac{4\alpha }{2}\text{sin}\frac{11\alpha }{2}+\text{sin}\frac{5\alpha }{2}\text{sin}\frac{10\alpha }{2}\right)\mathrm{.}}\hfill \end{array}}$ Mindegyik szorzat második tényezője egy tompaszög színusza; ezt a kiegészítő hegyes szög színuszával helyettesítve $\begin{array}{c}{\displaystyle t=\text{sin}\alpha +\frac{\text{sin}\frac{2\alpha }{2}\text{sin}\frac{3\alpha }{2}}{\text{sin}\frac{\alpha }{2}}+\frac{\text{sin}\frac{3\alpha }{2}\text{sin}\frac{4\alpha }{2}}{\text{sin}\frac{\alpha }{2}}+\frac{\text{sin}\frac{4\alpha }{2}\text{sin}\frac{5\alpha }{2}}{\text{sin}\frac{\alpha }{2}}+\frac{\text{sin}\frac{5\alpha }{2}\text{sin}\frac{6\alpha }{2}}{\text{sin}\frac{\alpha }{2}}\mathrm{.}}\end{array}$ Mármost a $\begin{array}{c}{\displaystyle \text{sin}x+\text{sin}2x+\text{sin}3x+\text{...}+\text{sin}nx=\frac{\text{sin}n\cdot \frac{x}{2}\cdot \text{sin}\left(n+1\right)\cdot \frac{x}{2}}{\text{sin}\frac{x}{2}}}\end{array}$ azonosság1 felhasználásával a jobb oldal $2$., $3$., $4$. és $5$. tagja rendre $n=2$, $3$, $4$, ill. $5$ értékkel $2$, $3$, $4$, ill. $5$ tagú összegként írható, és összevonás után (1)-et kapjuk.     Péli Katalin (Makó, József A. g. III. o. t.) 1Lásd pl. Faragó László: Matematikai szakköri feladatgyűjtemény (Középiskolai Szakköri Füzetek), 3. kiadás, Tankönyvkiadó, Budapest, 1963, 56. o., 526. feladat.