I. Az $AM$, $MB$ szakaszokat először egyirányúaknak tekintjük. Az állandó $AM\cdot MB$ érték mértani középarányosuknak $c$-nek négyzete, $AM\cdot MB=c^2$. Feltesszük, hogy $c>0$ (ugyanis $c=0$ esetén $AM=0$, az $A$ pont állandóan $M$-ben van, így $B$ az $M$-nek tükörképe $F$-re vonatkozóan, s ebből tüstént adódik, hogy $B$ mértani helye az adott $k$ kör 2-szeresre nagyított képe az $M$ hasonlósági középpontból). Eszerint $M$ mindig elválasztja 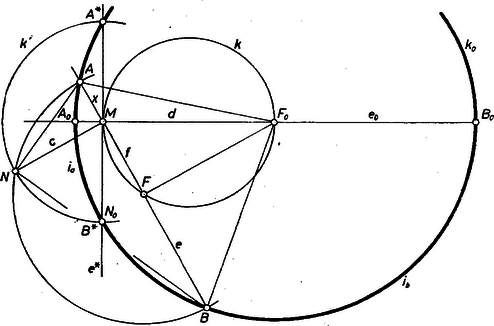$A$-t $F$-től és $B$-től.
Nyilvánvaló, hogy $e$ bármely helyzetében $F$ az $e$-nek $k$-val való, $M$-től különböző metszéspontja. Minden helyzetben $M$, $F$, $c^2$ és az $AM<MB$ feltétel egyértelműen meghatározza $A$ és $B$ helyzetét. A derékszögű háromszög magasságáról ismert mértani középarányos tételre gondolva egy megfelelő $A$, $B$ pontpárt úgy kapunk, hogy az $e$-re $M$-ben emelt merőlegesre fölmérjük az $MN=c$ szakaszt, kört írunk $F$ körül $FN$ sugárral, ennek az $FM$ félegyenesen levő metszéspontja $A$, $e$-vel való másik metszéspontja $B$ (1. ábra).

 

1. ábra

 

AM=x(>0), ekkor $MB=MF+FB=MF+AF=AM+2MF=x+2f$, az $x\left(x+2f\right)=c^2$ követelményből $x^2+2fx-c^2=0$, ennek gyökei valósak és ellentétes előjelűek, hiszen szorzatuk negatív, és a negatív gyök nem használható. Az adódó $x=\sqrt[]{f^2+c^2}-f$ kifejezésből is kiolvasható $A$ fenti szerkesztése.
$e$-nek csak az az $e^{*}$ helyzete kivételes, amely érinti $k$-t, ekkor ugyanis $F^{*}$ azonos $M$-mel és a mondott eljárás szerint kapott $A^{*}$, $B^{*}$ pontpárra az $A^{*}M=M{B}^{*}=c$ egyenlőség teljesül, és ezt a feladat kizárta.
Az $e$ néhány helyzetében így szerkesztett $A$, $B$ pontpárok egy $k_0$ körön látszanak sorakozni, melynek középpontja $M$-nek $k$-beli átellenes pontja, $F_0$. (Az $N$ pontok mindig az $M$ körüli $c$ sugarú $k\text{'}$ körön adódnak.) Bebizonyítjuk, hogy $e$ minden megengedett helyzetében $F_{0}A=F_{0}B$, állandó.
$e$-ként az $M{F}_0=e_0$ egyenest véve legyenek a fenti eljárás során kapott pontok $N_0$, $A_0$, $B_0$, így

$\begin{array}{c}{\displaystyle F_0{A}_0^2=F_0{B}_0^2=F_0{N}_0^2=F_0{M}^2+M{N}_0^2=d^2+c^2\mathrm{,}}\end{array}$

(1)

ahol $d$ a $k$ átmérője. $e$ minden más, megengedett helyzetében $F$ az $F_0$ merőleges vetülete $e$-n (Thalész), és $FA=FB$ folytán $F_{0}A=F_{0}B$. Továbbá

$\begin{array}{c}{\displaystyle F_0{B}^2=F_0{F}^2+F{B}^2=F_0{F}^2+{\left(MB-MF\right)}^2=\left(F_0{F}^2+M{F}^2\right)+MB\left(MB-2MF\right)\mathrm{,}}\end{array}$

és itt az első zárójelben $F_0{M}^2=d^2$ áll, a második zárójel pedig

$\begin{array}{c}{\displaystyle \left(MB-MF\right)-MF=FB-MF=AF-MF=AM\mathrm{,}}\end{array}$

tehát, felhasználva (1)-et:

$\begin{array}{c}{\displaystyle F_0{B}^2=d^2+MB\cdot AM=d^2+c^2=F_0{A}_0^2\mathrm{,}}\end{array}$

ami állításunkat igazolja, $A$ és $B$ a mondott $k_0$ kör pontjai. Ugyanez $A^{*}$-ra és $B^{*}$-ra is áll, és $e^{*}$ $\perp$ $e_0$ miatt mindegyikük játszhatja a fenti $N_0$ szerepét.
Pontosabban ezt találtuk: mivel $M$ elválasztja $A$-t $F$-től, vagyis $k$-tól, azért $e^{*}$ is elválasztja $A$-t $k$-tól, $A$ a $k_0$-nak félkörnél kisebb $A^{*}{B}^{*}=i_a$ ívén van, $B$ pedig a félkörnél nagyobb $A^{*}{B}^{*}=i_b$ ívén.
Bebizonyítjuk, hogy megfordítva, ha $e$-nek egy tetszés szerinti (de $e^{*}$-tól különböző) $e\text{'}$ helyzete $i_a$-t $A\text{'}$-ben, $i_b$-t $B\text{'}$-ben metszi, akkor teljesül $A\text{'}M\cdot MB\text{'}=c^2$, és az $A\text{'}B\text{'}$ szakasz $F\text{'}$ felezőpontja rajta van $k$-n. Valóban, $e\text{'}$ és $e^{*}$ a $k_0$-nak $M$-en átmenő és egymástól különböző szelői, ezért $A\text{'}M\cdot MB\text{'}=A^{*}M\cdot M{B}^{*}=c^2$. Továbbá $F_{0}F\text{'}A\text{'}\sphericalangle =F_{0}F\text{'}M\sphericalangle$ derékszög, tehát $F\text{'}$ rajta van az $M{F}_0$ átmérőjű Thalész körön, vagyis $k$-n.
Ezek szerint az $A$-t és $B$-t szétválasztó $M$ pont esetére $A$ és $B$ mértani helye a fent leírt $k_0$ körnek $i_a$ ill. $i_b$ íve, az ívek $A^{*}$, $B^{*}$ végpontjai nem tartoznak hozzá a mértani helyhez.

 

II. $MA$-t és $MB$-t egyirányúaknak véve a pontok sorrendje $M$, $A$, $F$, $B$. Legyen ismét $MA=x$, és $MF=f=\left(MA+MB\right)/2$, így $MB=2f-x$ és $0<x<f$, továbbá $MA\cdot MB=c^2$. A követelmény: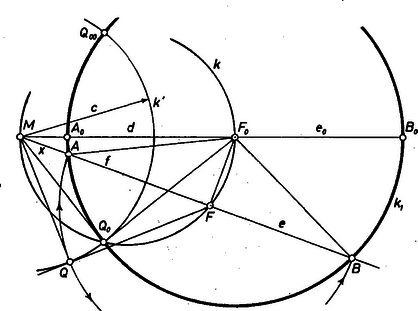

$\begin{array}{c}{\displaystyle c^2-x\left(2f-x\right)=x^2-2fx+c^2=\mathrm{0,}}\end{array}$

innen $x=f-\sqrt[]{f^2-c^2}$ (2. ábra).

 

 

2. ábra

 

Eszerint az $F$-ből az $M$ körüli $c$ sugarú $k\text{'}$ körhöz húzott $FQ$ érintőszakasszal mint sugárral rajzolt kör metszi ki $e$-ből $F$ és $M$ között $A$-t és $F$-en túl $B$-t.
$e$-nek több helyzete alapján az $A$ és $B$ pontokból ismét egy $k_1$ körnek két íve rajzolódik ki, középpontja a fenti $F_0$, átmérője az $M{F}_0=e_0$ helyzetben adódó $A_0{B}_0$ szakasz. $e$-t az $M{F}_0=e_0$ helyzettől egyre jobban elfordítva $MF=f$ csökken, és ha $F$-ként $k$ és $k\text{'}$ metszéspontját választjuk, vagyis ha $f=c$, akkor $A$ is, $B$ is $Q_0$ ban adódik, amit a követelmény kizárt. További elfordítás esetén (az $e_0$-ra merőleges helyzetig) nincs $A$, $B$ pontpár, mert $MF<c$.
Valóban, $e_0$ esetén $f=M{F}_0=d$ és $F_0{A}_0^2=F_0{B}_0^2=F_0{Q}_0^2=d^2-c^2$, általában pedig $F_{0}F\perp e$ és $FA=FB$ miatt $F_{0}A=F_{0}B$, így

$\begin{array}{c}{\displaystyle F_0{A}^2=F_0{F}^2+F{A}^2=F_0{F}^2+F{Q}^2=\left(F_0{F}^2+F{M}^2\right)-M{Q}^2=d^2-c^2=F_0{A}_0^2\mathrm{.}}\end{array}$

Pontosabban: $A$ a $k_1$ kör kisebb $Q_0{Q}_{00}$ ívének belső pontja ‐ ahol $Q_{00}$ a $Q_0$ tükörképe $e_0$-ra ‐, $B$ pedig a nagyobb $Q_0{Q}_{00}$ ív belső pontja ($M{Q}_0$ érinti $k_1$-et).
Az I. eset befejezéséhez hasonlóan belátható, hogy a mondott ívek minden belső pontja kiadódik $A$-ként, ill. $B$-ként, tehát $A$ és $B$ mértani helye a mondott két ív, a végpontok nélkül.
Ha $c\geqq d$, azaz $k\text{'}$ magába zárja az adott $k$ kört, akkor egyetlen $A$, $B$ pontpár sem jön létre.
 Tátray Péter (Budapest, Berzsenyi D. Gimnázium)
 Moson Péter (Budapest, Fazekas M. Gyak. Gimnázium)

 

Megjegyzés. Az érdeklődőknek ajánljuk, keressék meg a kapcsolatot ezen feladat és az 1056. gyakorlat¹ között.

---

¹K. M. L. 34 (1967) 70. o.