Kezdőlap


Feladat:	1528. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Lengyel Erzsébet , Somogyi Árpád
Füzet:	1968/január, 10 - 12. oldal		PDF \| MathML
Témakör(ök):	Szabályos sokszög alapú gúlák, Kocka, Szerkesztések a térben, Feladat
Hivatkozás(ok):	Feladatok: 1967/március: 1528. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. 1. Legyen a keresett kockának az adott $e$ -t tartalmazó lapja. $E F G H$ , az $e$ -n fekvő lap‐átló $F H$ , a szemben levő lap pedig $A B C D$ úgy, hogy a kocka hátra levő élei 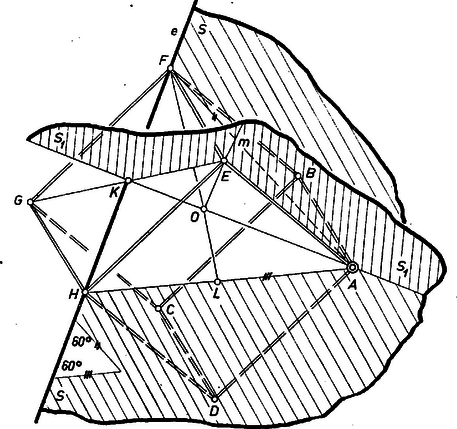$A E$ , $B F$ , $C G$ , $D H$ .
$F A$ és $H A$ szintén lapbeli átlók, hosszuk egyenlő $F H$ -val, ezért $F H A$ egyenlő oldalú háromszög, benne fekszik az $e$ és $A$ által meghatározott $S$ síkban.

1. ábra

E A

E F

és

E H

a kocka élei, egyenlők, ezért

A F H E

szabályos háromoldalú gúla,

E

főcsúcsa rajta van az

A F H

alap

O

középpontjában

S

-re állított merőlegesen. Továbbá az

A E O = S_{1}

sík e gúlának szimmetriasíkja, tehát

F H

-t a

K

felezőpontjában metszi, ez az

E F G H

lap középpontja, az

E G

lapátlót is felezi, és így

K E = E G / 2 = F H / 2 = K F

.
2. Ezek alapján a szerkesztés a következő. Az

S

síkban

e

-nek tetszés szerinti szakasza fölé egyenlő oldalú háromszöget szerkesztünk, majd újabb két oldalával párhuzamost húzunk

A

-n át, ezek

e

-ből kimetszik az

F

, ill.

H

csúcsot. Megfelezzük az

F H

H A

oldalt a

K

,-ill.

L

ponttal, ekkor

A K

és

F L

metszéspontja

O

O

-n át

m

merőleges egyenest állítunk

S

-re, majd az

A

és

m

által meghatározott

S_{1}

síkban

K

körül

K F

sugárral írt körrel

m

-ből kimetsszük

E

-t. A hátra levő csúcsokat hárnmszögeknek paralelogrammává való kiegészítésével kapjuk:

A E F

-ből

B

-t,

F E H

-ból

G

-t,

H E A

-ból

D

-t, végül pl.

B A D

-ból

C

-t.

3. Alakzatunk valóban kocka. Ugyanis

S_{1}

merőleges

S

-re; metszésvonaluk

A K

, erre merőlegesen áll

F H

, így

F H

merőleges

S_{1}

-re, tehát az

S_{1}

-beli

K E

-re is. Ezért

E F G H

, mint egymásra merőleges és egyenlő hosszú átlókkal bíró paralelogramma, négyzet. Ugyanez áll

E A B F

-re és

E H D A

-ra, mert ezek előállíthatók

E F G H

-ból

E O

körüli

120^{\circ}

-os forgatással. Az utoljára szerkesztett

C

csúcs benne van a

G H D

és a

G F B

síkban is, mert szerkesztésünk szerint

D C # A B # E F # H G

és

B C # A D # E H # F G

, és a mondott háromszögeket egyenlőoldalú paralelogrammává egészíti ki. Ezek négyzetek, úgyszintén

A B C D

is, mert mindegyik szögük egyállású a fentebbi 3 négyzet egyik szögével.

4. A szerkesztés mindig végrehajtható, ha

A

nincs rajta

e

-n, mert a felhasznált kör metszi

m

-et. Ugyanis,

K A = d

jelöléssel

K O = d / 3

K E = K F = d / \sqrt[]{3}

, így

K E > K O

E

számára 2 metszéspont adódik, a belőlük származtatott 2 kocka egymás tükörképe

S

-re.
Lengyel Erzsébet (Budapest, Berzsenyi D. g. I. o. t.) és
Somogyi Árpád (Budapest, Fazekas M. gyak. g. II. o. t.)
dolgozatából, a bizonyítással kiegészítve

Megjegyzések. 1. Az

m

egyenest az alábbiak szerint szerkeszthetjük, mindig csak síkbeli szerkesztést végezve.

m

-et megadja pl. annak a 2 síknak a metszésvonala, mely átmegy

O

-n és merőleges

A K

-ra, ill.

F L

-re. Egy ilyen síkot, pl. az

A K

-ra merőlegesen állót, két az

O

-n átmenő egyenesével határozunk meg: felveszünk

A K

-n át 2 különböző síkot ‐ egyikük lehet pl.

S

‐ és mindegyikben megszerkesztjük az

O

-n átmenő,

A K

-ra merőleges egyenest. Ezek után a két merőleges síknak egy az

O

-tól különböző közös pontját, vagyis

m

egy további pontját úgy kapjuk, hogy az

A K

-ra merőleges síknak egy

O

-t nem tartalmazó egyenesén megkeressük az

F L

-re merőleges síkkal való döféspontot. (Az utolsó lépésre, ti. az egyenes és a sík metszéspontjának meghatározására a térbeli szerkesztésekben az a megállapodás, hogy ha az egyenes és a sík adottak és tudjuk, hogy van metszéspontjuk ‐ vagyis az egyenes nincs benne a síkban és nem is párhuzamos vele ‐, akkor a metszéspontot is adottnak tekintjük.)
2.

E

-t

m

-ből kimetszhetjük az

A K

szakasz fölé írt Thalész‐körrel is. Ekkor a szerkesztés helyességének bizonyításában számításra van szükség:

K A = F H \cdot \sqrt[]{3} / 2

K O = K A / 3

, és mértani középarányosukként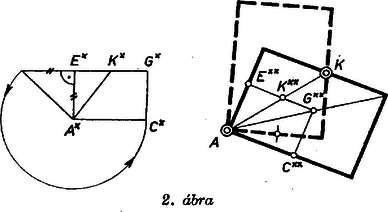

K E^{2} = K A \cdot K O = K A^{2} / 3 = F H^{2} / 4

K E = F H / 2

II. megoldás (vázlat). Az

A

-n átmenő és az

e

-re merőleges

S_{1}

sík metszéspontja

K

, e sík a kockából az

A E G C

téglalapot metszi ki, melyben

A E : E G = 1 : \sqrt[]{2}

és

K

felezi

E G

-t. Eszerint az

A K

szakaszhoz hasonlósági transzformációval megszerkeszthetjük a téglalapot. (Egy tetszés szerinti egyenlő szárú derékszögű háromszög befogójával és átfogójával, mint oldalakkal,

A^{*} E^{*} G^{*} C^{*}

téglalapot szerkesztünk, vesszük az

E^{*} G^{*} (= A^{*} E^{*} \cdot \sqrt[]{2})

oldal

K^{*}

felezőpontját,

A^{*} K^{*}

-ot fölmérjük az

A K

félegyenesre az

A K^{* *}

helyzetbe, az

A K^{*} E^{*}

háromszöget, majd a téglalapot átmásoljuk az

A K^{* *} E^{* *}

, ill.

A E^{* *} G^{* *} C^{* *}

helyzetbe, végül ezt nagyítva kapjuk

A E G C

-t.) Ebből pedig

K

-n átmenő középvonala körüli

90^{\circ}

-os elfordítással megkapjuk a további 4 csúcsot.