Kezdőlap


Feladat:	1527. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Andor Csaba , Balogh J. , Bán Ilona , Baróthy B. , Berács J. , Berkes Z. , Bodor I. , Bulkai T. , Csóka G. , Dombi J. , Draschitz R. , Élthes Eszter , Gegesy F. , Gerő P. , Hegedűs A. , Horváth S. , Hunyadvári L. , Joó I. , Juhász Ágnes , Kecskeméty K. , Kocsis F. , Lakatos L. , Lublóy L. , Mészáros J. , Mitrocsák Anikó. , Moson P. , Munk S. , Nagy E. , Nagy Zs. , Orbán G. , Péceli G. , Péli Katalin , Perémy G. , Pintér Ágnes , Rácz Éva , Radó P. , Sásdy B. , Sergyán Stefánia , Somos E. , Szabó Klára , Szenes Katalin , Tabiczky I. , Takács L. , Tátray P. , Varró Z. , Vass Erzsébet , Végvári L. , Vetier A. , Zambó Péter , Zima E. , Zöldy B.
Füzet:	1968/március, 99 - 102. oldal		PDF \| MathML
Témakör(ök):	Háromszög alapú hasábok, Síkgeometriai számítások trigonometria nélkül háromszögekben, Térelemek és részeik, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1967/március: 1527. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Háromszögben metszik a hasábot az oldaléleket metsző síkok és az egy csúcsot lemetsző síkok. Keressünk először az első típusba tartozó síkot, egyelőre tetszés szerinti $a$ , $b$ , $c$ alapélű hasábra, ahol $a \leq b \leq c$ . Legyen a kimetszett $H$ egyenlő oldalú háromszög oldala $d$ . Így az $a$ , $b$ , $c$ szélességű oldallapon levő metszetoldal végpontjainak magasságkülönbsége rendre

\begin{matrix} \sqrt[]{d^{2} - a^{2}} = x, \sqrt[]{d^{2} - b^{2}} = y, \sqrt[]{d^{2} - c^{2}} = z, \end{matrix}

(1)

és ezekre

x \geq y \geq z (\geq 0)

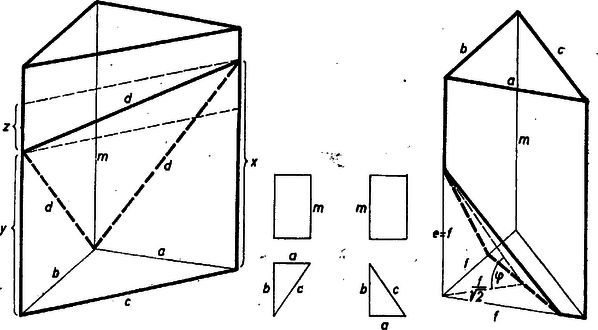1. ábra 2 ábra

Ennélfogva (1. ábra):

\begin{matrix} x = y + z, \end{matrix}

(2)

hiszen

H

alsó és felső csúcsának magasságkülönbsége a legnagyobb, és ennyit emelkedünk akkor is, ha a közbülső magasságú csúcson át,

H

-nak további két oldalán megyünk föl a felső csúcsba. (1) szerint

\begin{matrix} a^{2} + x^{2} = b^{2} + y^{2} = c^{2} + z^{2} (= d^{2}) . \end{matrix}

(3)

A szélső kifejezésekből (2) alapján

\begin{matrix} a^{2} + {(y + z)}^{2} = c^{2} + z^{2}, z = \frac{c^{2} - a^{2}}{2 y} - \frac{y}{2} \end{matrix}

(föltehetjük ugyanis, hogy

y \neq 0

, mert különben

z = 0

és (2)-ből

x = 0

, ami csak

a = b = c

esetén következik be, és ekkor a keresett sík nyilvánvalóan párhuzamos kell, hogy legyen az alappal). Ekkor (3)-ból, a szokásos rendezési lépésekkel

y^{2}

-re kapunk másodfokú egyenletet:

\begin{matrix} b^{2} + y^{2} = c^{2} + \frac{{(c^{2} - a^{2})}^{2}}{4 y^{2}} - \frac{c^{2} - a^{2}}{2} + \frac{y^{2}}{4}, \\ 3 y^{4} - 2 (a^{2} + c^{2} - 2 b^{2}) y^{2} - {(c^{2} - a^{2})}^{2} = 0. \end{matrix}

y^{2}

-re adódó két gyök szorzata

- {(c^{2} - a^{2})}^{2} / 3 < 0

, tehát a kisebb gyök negatív, ezt természetesen figyelmen kívül hagyjuk.
A diszkrimináns

1 / 4

része:

\begin{matrix} {(a^{2} + c^{2} - 2 b^{2})}^{2} + 3 {(c^{2} - a^{2})}^{2} = 4 (a^{4} + b^{4} + c^{4}) - 4 (a^{2} b^{2} + a^{2} c^{2} + b^{2} c^{2}) . \end{matrix}

Jelöljük a jobb oldal első zárójelbeli kifejezését

S_{4}

-gyel, a másodikbelit

S_{22}

-vel, így

\begin{matrix} y^{2} = \frac{1}{3} (a^{2} + c^{2} - 2 b^{2} + 2 \sqrt[]{S_{4} - S_{22}}) és \\ d^{2} = y^{2} + b^{2} = \frac{1}{3} (a^{2} + b^{2} + c^{2} + 2 \sqrt[]{S_{4} - S_{22}}) . \end{matrix}

Ilyen metszet természetesen csak akkor lehetséges, ha a hasáb

m

magassága legalább

x

, azaz

\begin{matrix} m^{2} \geq \frac{1}{3} (b^{2} + c^{2} - 2 a^{2} + 2 \sqrt[]{S_{4} - S_{22}}) . \end{matrix}

II.

H

oldalának ismeretében kifejezhetjük területét, ekkor pedig

S

és az alapsík

φ

hajlásszögének koszinuszát egy ismert tétel szerint megadja az alapidom és

H

területének hányadosa:

\begin{matrix} cos φ = t : \frac{d^{2} \sqrt[]{3}}{4}, \end{matrix}

ahol

t

kiszámítható pl. Heron képlete alapján.

III. Az adott numerikus esetben az alapidom derékszögű háromszög. Így

t = 6

, másrészt

d^{2} = (50 + 2 \sqrt[]{193}) / 3

és

cos φ = \frac{25 \sqrt[]{3} - \sqrt[]{579}}{36} = 0, 5344

\begin{matrix} φ = 57, 7^{\circ} . \end{matrix}

IV. A hasáb alapidomát is átmetsző síkmetszet kérdését csak az adott numerikus esetben tekintjük.

H

két oldala a hasáb két oldallapjából egy-egy derékszögű háromszöget metsz le, és ezek egybevágók, hiszen az oldalélen levő

e

befogójuk közös, átfogójuk pedig

d

(2. ábra). Így a másik befogók, a lemetszett alapcsúcsba befutó alapélek részei, szintén egyenlők ‐ legyen a hosszuk

f

‐, tehát síkunk az alapháromszögből egyenlő szárú háromszöget metsz le. Ebből már adódik, hogy a lemetszett csúcs csak a derékszög csúcsa lehet. Ugyanis a két hegyesszög kisebb

60^{\circ}

-nál

(cos β = 0, 6 > 0, 5 = cos 60^{\circ})

, így az egyenlő szárú háromszög alapja nem lehet

d

, hiszen kisebb

f

-nél, ez pedig kisebb, mint

d

.
Ekkor

S

síkunk a két oldallapból egybevágó derékszögű háromszöget metsz le, és a föntebbi meggondolás szerint az alapból lemetszett háromszög is egybevágó a másik kettővel. Így

S

mindhárom élből ugyanakkora

f

szakaszt metsz le, az alapból lemetszett háromszög szimmetriatengelye

f / \sqrt[]{2}

, tehát a

φ'

hajlásszögre

\begin{matrix} tg φ' = \frac{f}{f / \sqrt[]{2}} = \sqrt[]{2}, φ' = 54, 74^{\circ} . \end{matrix}

A metsző síknak nem lehet metszetszakasza a hasáb alaplapján is, fedőlapján is, mert így a metszetnek legalább

4

csúcsa lenne. Ezért további lehetőség nincs.

Andor Csaba (Budapest, Berzsenyi D. g. III. o. t.)

Megjegyzés. S. Lhuilier francia matematikus (1750‐1840) bebizonyította, hogy tetszés szerinti háromoldalú hasáb síkmetszetei között minden lehetséges háromszög-alak előfordul¹.

II. megoldás (csak az oldaléleket átmetsző sík esetére). Tekintsük

H

-nak

k

körülírt körét.

k

-nak az alapsíkon levő vetülete egy az alapháromszög köré írt ellipszis. Elég lenne ismerni ennek féltengelyeit ‐ a szokásos jelöléssel

a

-t és

b

-t, ezekkel ugyanis

cos φ = b / a

, mert

a

éppen

k

sugara, ti. az alapsíkkal párhuzamos sugár vetülete,

b

pedig ‐ az ellipszis legrövidebb átmérőjének fele ‐ annak a sugárnak a vetülete, amely a keresett

φ

-vel hajlik az alapsíkhoz.

a

-t és

b

-t kiszámíthatjuk az 1502. feladat² eljárásával az ellipszis egy konjugált fél-átmérőpárjának

r

r'

hosszából és a köztük levő

ψ

szögből. Ilyen értékhármast ad

k

bármely merőleges sugárpárjának az alapsíkon levő vetülete. Vegyük egyiknek a

H

valamelyik csúcsához tartozó sugarat; ennek vetülete az alapháromszög megfelelő csúcsából induló súlyvonalnak a csúcs felé eső

2 / 3

része. Ugyanis

k

középpontja a

H

-nak egyszersmind súlypontja, és ez a tulajdonság a vetületben is megmarad (mert az egy egyenesen levő szakaszok vetületeinek aránya egyenlő az eredeti szakaszok arányával, ezért az oldalfelező pont vetülete felezi a megfelelő oldalvetületét, és a súlyvonal harmadolópontjának vetülete harmadolja a súlyvonal vetületét). A

H

mondott sugarára merőleges sugár vetülete arra az egyenesre esik, amely átmegy az alapháromszög súlypontján és párhuzamos a kiszemelt csúcsával szemben levő oldallal, mert párhuzamos egyenesek vetületei párhuzamosak. A mondott sugár

\sqrt[]{3}

-szor akkora, mint a

H

belsejében levő része. Ezért az alapon a megfelelő félátmérő is

\sqrt[]{3}

-szor akkora, mint a mondott egyenesből a súlypont és a háromszög kerülete közé eső szakasz, vagyis az oldal

1 / \sqrt[]{3}

része, hiszen a háromszögbeli szakasz egyszerű számítás szerint az oldal

1 / 3

rés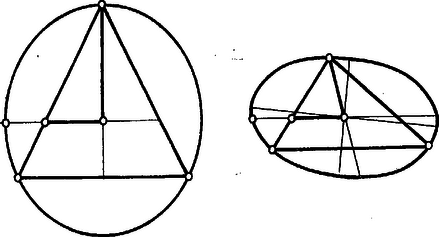ze.

3. ábra

A számpélda esetére szorítkozva induljunk ki

H

-nak abból a csúcsából, melynek vetülete az alapháromszög derékszögének csúcsa; így a súlyvonal fele az átfogónak és az ellipszis két konjugált félátmérője

r = c / 3 = 5 / 3

r' = 5 / \sqrt[]{3}

és a köztük levő

ψ

hegyesszög

2

-szer akkora, mint az alapháromszög kisebbik hegyes szöge:

sin ψ / 2 = 3 / 5

cos ψ / 2 = 4 / 5

, így

sin ψ = 24 / 25

.
Most már az idézett feladat (3) képleteivel

\begin{matrix} \sqrt[]{r^{2} + r'^{2} + 2 r r' sin ψ} = \frac{2}{3} \sqrt[]{25 + 12 \sqrt[]{3}}, \\ \sqrt[]{r^{2} + r'^{2} - 2 r r' sin ψ} = \frac{2}{3} \sqrt[]{25 - 12 \sqrt[]{3}}, és így \\ cos φ = \frac{b}{a} = \frac{\sqrt[]{25 + 12 \sqrt[]{3}} - \sqrt[]{25 - 12 \sqrt[]{3}}}{\sqrt[]{25 + 12 \sqrt[]{3}} + \sqrt[]{25 - 12 \sqrt[]{3}}} = \\ = \frac{1}{24 \sqrt[]{3}} {(\sqrt[]{25 + 12 \sqrt[]{3}} - \sqrt[]{25 - 12 \sqrt[]{3}})}^{2} = \frac{25 - \sqrt[]{193}}{12 \sqrt[]{3}}, \end{matrix}

amit az I. megoldásban is találtunk.

Megjegyzés. A súlypontnak és a rajta átmenő szakasz végpontjának

H

-hoz való csatolása lényegében hasonló ahhoz, ahogyan az 1424. feladat ³ I. megoldásában és a hozzá fűzött megjegyzésekben a szabályos nyolcszöghöz kapcsoltunk hozzá további, a vetületben megszerkeszthető pontokat.

¹Lásd pl. H. Dörrie: A diadalmas matematika, Száz híres probléma két évezred matematikai műveltségéből, Gondolat Kiadó, Budapest, 1965, 324. o.

²K. M. L. 35 (1967) 206. o.

³K. M. L. 32 (1966) 212. o.