Kezdőlap


Feladat:	1519. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Balogh J. , Borzsák P. , Csörgei J. , Csörgő Piroska , Draschitz R. , Fuggerth E. , Halász F. , Halek T. , Hunyadvári L. , Katona V. , Koren A. , Lakatos L. , Lempert L. , Martoni V. , Nagy Zs. , Pap Márta , Papp E. , Péceli G. , Perámy G. , Pintz J. , Takács L. , Tátray P. , Tóth Ferenc , Zambó Péter
Füzet:	1967/október, 62 - 63. oldal		PDF \| MathML
Témakör(ök):	Négyszög alapú gúlák, Derékszögű háromszögek geometriája, Deltoidok, Feladat
Hivatkozás(ok):	Feladatok: 1967/február: 1519. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ahhoz, hogy a gúla köré gömböt lehessen írni, alapdeltoidjának húrnégyszögnek kell lennie. Ha ez teljesül, akkor lehet is gömböt írni a gúla köré. Jelöljük ugyanis a deltoid köré írt kört $k$ -val; középpontját $K$ -val, a gúlának a deltoid fölötti csúcsát $M$ -mel; ekkor a $K M$ egyenesen átmenő, és az alap $S$ síkjára merőleges sík $k$ -ból egy $A C$ átmérőt metsz ki, és az $A C M$ háromszög köré írt $k_{1}$ kör $O$ középpontja rajta van a $K$ -ban $S$ -re állított merőlegesen. Így pedig $k$ minden pontja ugyanannyira van $O$ -tól, mint pl. $A$ , és ugyanennyire van $M$ is $O$ -tól, tehát az $O$ körüli $O$ M sugarú gömb átmegy a gúla mindegyik csúcsán.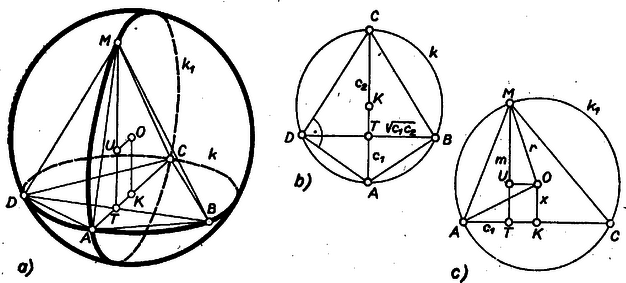

Az alapdeltoid

c_{1}

c_{2}

részekre osztott átlója szimmetriatengely, mert a másik ‐ rá merőleges ‐ átlót két egyenlő részre osztja. Ez az átló a deltoidot két derékszögű háromszögre bontja, mert a háromszögnek az átlót

c_{1}

c_{2}

részekre bontó magassága

\sqrt[]{c_{1} c_{2}}

hosszúságú, ez pedig az ismert mértani középarányossági tétel szerint a derékszögű háromszögre teljesül, és más háromszögre nem. Így a deltoid húrdeltoid.
Legyen az alapidom átlóinak metszéspontja

T

O

vetülete az

M T

egyenesen

U

K O = x

és

O A = r

(ha

O

S

alatt van, akkor

x < 0

). Így az

M O U

derékszögű háromszögben

M U = m - x

O U = K T = | c_{1} - c_{2} | / 2

, az

O A K

háromszögben pedig

A K = (c_{1} + c_{2}) / 2

, ennélfogva

\begin{matrix} r^{2} = {(m - x)}^{2} + \frac{{(c_{1} - c_{2})}^{2}}{4}, r^{2} = x^{2} + \frac{{(c_{1} + c_{2})}^{2}}{4}, \end{matrix}

amiből egyrészt kivonással

\begin{matrix} x = \frac{m^{2} - c_{1} c_{2}}{2 m} = \frac{m}{2} - \frac{c_{1} c_{2}}{2 m}, \end{matrix}

másrészt visszahelyettesítéssel

\begin{matrix} r^{2} = \frac{m^{2}}{4} + \frac{c_{1}^{2} c_{2}^{2}}{4 m^{2}} + \frac{c_{1}^{2}}{4} + \frac{c_{2}^{2}}{4} = \frac{1}{4 m^{2}} (m^{2} + c_{1}^{2}) (m^{2} + c_{2}^{2}), \end{matrix}

végül

r = M A \cdot M C / 2 m

K O

első kifejezése szerint

2 m x = T M^{2} - T B^{2}

, vagyis

O

az alapsík fölött, rajta, ill. alatta adódik aszerint, hogy

T M ⋛ T B

Pap Márta (Budapest, Kölcsey F. g. III. o. t.)