Kezdőlap


Feladat:	1517. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Hegedűs András , Munk Sándor , Rácz Éva
Füzet:	1968/január, 8 - 10. oldal		PDF \| MathML
Témakör(ök):	Háromszögek egybevágósága, Háromszögek hasonlósága, Pont körüli forgatás, Egyenesek egyenlete, Pont és egyenes távolsága, Síkgeometriai számítások trigonometria nélkül háromszögekben, Feladat
Hivatkozás(ok):	Feladatok: 1967/február: 1517. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen a kérdéses négyzet $A B C D$ , a többiektől elválasztott csúcs $A$ , a csúcsok és az $O$ középpont $e$ -től mért távolsága rendre, $a$ , $b$ , $c$ , $d$ , $x$ . A feladat feltevése szerint $a c = b d$ . Föltehetjük, hogy $b ≦ d$ , mert ezt, ha kell, a $B$ , $D$ betűk fölcserélésével elérhetjük. Így $e$ a $D B$ átlónak $B$ -n túli meghoszszabbítását metszi, $b = d$ esetén pedig párhuzamos vele.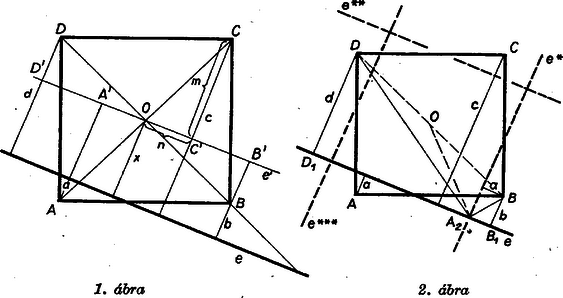

Húzzuk meg

O

-n át az

e

-vel párhuzamos

e'

egyenest, és legyen ezen a csúcsok vetülete rendre

A'

B'

C'

D'

b < d

esetén

B

e'

-nek azon a partján van, mint

A

, az

O A A'

O B B'

O C C'

O D D'

derékszögű háromszögek egybevágók, mert átfogójuk

1 / \sqrt[]{2}

és hegyesszögeik egyenlők. Legyenek a befogóik

m

és

n

, ahol

m > n

. Ezekkel

\begin{matrix} a + x = A A' = C C' = c - x = m, \\ x - b = B B' = D D' = d - x = n, \\ így & a = m - x, c = m + x, b = x - n, d = x + n, \end{matrix}

Ezeket a föltevésbe helyettesítve

\begin{matrix} m^{2} - x^{2} = x^{2} - n^{2}, x^{2} = \frac{1}{2} (m^{2} + n^{2}) = \frac{1}{4}, x = \frac{1}{2} . \end{matrix}

Ha pedig

b = d

, akkor

e'

azonos a

B D

egyenessel, tehát

x = b = d

a + x = c - x = 1 / \sqrt[]{2}

, innen

a = 1 / \sqrt[]{2} - x

c = 1 / \sqrt[]{2} + x

, és a föltevésből ismét

x = 1 / 2

.
Hegedűs András (Budapest, Apáczai Csere J. gyak. g. III. o. t.)

II. megoldás. Forgassuk el az ábrát a négyzet

O

középpontja körül

90^{\circ}

-kal úgy, hogy

A

B

-be jusson. Legyen

B

és

D

vetülete

e

-n

B_{1}

, ill.

D_{1}

e

elforgatottjának,

e^{*}

-nak a metszéspontja

e

-vel

A_{2}

. Ekkor

A_{2} B_{1} = a

, mert egyenlő

A

elforgatottjának,

B

-nek

e^{*}

-tól való távolságával. Hasonlóan

A_{2} D_{1} = c

. A feltétel szerint

a c = b d

, így az

A_{2} B B_{1}

és

D A_{2} D_{1}

derékszögű háromszögek befogóinak aránya

\begin{matrix} \frac{A_{2} B_{1}}{B_{1} B} = \frac{a}{b} = \frac{d}{c} = \frac{D D_{1}}{D_{1} A_{2}} . \end{matrix}

Így a két háromszög hasonló. Mivel továbbá a megfelelő csúcsokon végighaladva a két háromszöget egyező irányban járjuk körül és megfelelő befogóik merőlegesek, így átfogóik is:

D A_{2} B ∢ = 90^{\circ}

. A

D A_{2} B

derékszögű háromszög

O A_{2}

súlyvonala az átfogó felével, vagyis a négyzet átlójának a felével egyenlő.
Továbbforgatva az ábrát

90^{\circ} - 90^{\circ}

-kal, az

e

egyenes elforgatottjai egy

O

középpontú négyzetet zárnak be, melynek átlója a bizonyítottak szerint egyenlő hosszú az

A B C D

négyzet átlójával, így a két négyzet egybevágó. És mivel középpontjuk közös, azért beírt körük is, vagyis

e

távolsága

O

-tól a négyzet oldalának fele.

III. megoldás. Helyezzünk koordináta‐rendszert ábránkra, legyenek a csúcsok koordinátái

A

(0, 0),

B

(1, 0),

C

(1, 1),

D

(0, 1) és

e

egyenlete

y = m x + b

, ahol

0 < b < 1

, mert

e

elválasztja

A

-t

D

-től. A csúcsok

e

-től mért előjeles távolsága az ismert képlet felhasználásával rendre

\begin{matrix} \frac{- b}{\sqrt[]{1 + m^{2}}}, \frac{- m - b}{\sqrt[]{1 + m^{2}}}, \frac{1 - m - b}{\sqrt[]{1 + m^{2}}}, \frac{1 - b}{\sqrt[]{1 + m^{2}}} . \end{matrix}

Feltevésünk a távolságok abszolut értékére vonatkozik, ezért

A

távolságának

- 1

-szeresét véve, a föltevés szerint, a közös nevezővel mindjárt szorozva

\begin{matrix} b (1 - m - b) = (m + b) (b - 1), amiből \\ b = \frac{1}{2} (1 - m) \pm \frac{1}{2} \sqrt[]{m^{2} + 1} . \end{matrix}

Ezt helyettesítjük

e

egyenletébe és a távolság‐képletet az (

1 / 2

1 / 2

) középpontra alkalmazzuk. A kívánt távolság:

\begin{matrix} x = \frac{| \frac{1}{2} - \frac{1}{2} m - \frac{1}{2} (1 - m) \mp \frac{1}{2} \sqrt[]{m^{2} + 1} |}{\sqrt[]{m^{2} + 1}} = \frac{1}{2} . \end{matrix}

Rácz Éva (Makó, József A. g. III. o. t.)
Munk Sándor (Budapest, II. Rákóczi F. g. III. o. t.)