Kezdőlap


Feladat:	1512. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bajmóczy E. , Berács J. , Bulkai T. , Fuggerth E. , Gegesy F. , Joó I. , Juhász Ágnes , Körmendi Sándor , Missura Éva , Molnár S. G. , Nagy Zs. , Perémy G. , Pintz J. , Sásdy B. , Somos E. , Sugár László , Takács L. , Végh Gy. , Wagner A. , Zöldy B.
Füzet:	1968/március, 97 - 99. oldal		PDF \| MathML
Témakör(ök):	Csonkagúlák, Egyenes körkúpok, Terület, felszín, Térfogat, Síkgeometriai számítások trigonometria nélkül négyszögekben, Síkgeometriai számítások trigonometria nélkül körökben, Feladat
Hivatkozás(ok):	Feladatok: 1967/január: 1512. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Legyen az alapidom magja az $A B C D = N$ négyzet, a csúcsokban álló oszlop felső végpontja rendre $A^{*}$ , $B^{*}$ , $C^{*}$ , $D^{*}$ úgy, hogy $A A^{*} = B B^{*} = a$ , $C C^{*} = D D^{*} = a / 2$ , az alapidomot határoló, $N$ csúcsai körüli ívek rendre $A_{1} A_{2}$ , $B_{1} B_{2}$ , $C_{1} C_{2}$ , $D_{1} D_{2}$ , az egyenesszakaszok $A_{2} B_{1}$ , $B_{2} C_{1}$ , $C_{2} D_{1}$ és $D_{2} A_{1}$ . A sátor szimmetrikus az $A B$ szakasz felező merőleges síkjára nézve. Az 1. ábra a sátor felülnézetét és oldalnézetét mutatja be.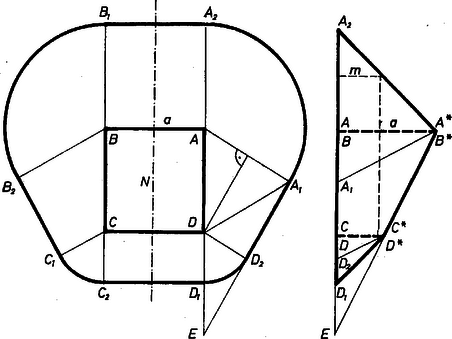

1. ábra

A A_{1} D_{2} D

derékszögű trapézban

D A A_{1} ∢ = 60^{\circ}

, mert a

D

-ből húzott magasság felezi az

A A_{1}

alapot, hiszen talppontjának

A_{1}

-től való távolsága

D D_{2}

-vel, azaz

a / 2

-vel egyenlő, így ez a magasság az

A

csúccsal egy szabályos háromszög felét adja. Másrészt

A_{2} B_{1} ∥ A B ∥ D_{1} C_{2}

A_{2}

és

D_{1}

A D

egyenesen van, az

A_{1} A_{2}

ív középponti szöge

120^{\circ}

, a

D_{1} D_{2}

ívé

60^{\circ}

, tehát hosszuk

a \cdot 2 π / 3

, ill.

a \cdot π / 6

.
A

D D_{2} D^{*}

derékszögű háromszög az

A A_{1} A^{*}

derékszögű háromszögnek

2 : 1

arányú kicsinyítettje. Nyilvánvaló ugyanis, hogy

A^{*} D^{*}

és

A_{1} D_{2}

A

-nak

D

-re vett

E

tükörképében metszik egymást, és a két háromszög síkja párhuzamos, mert

A

-nál, ill.

D

-nél levő szögeik egyállásúak. Eszerint

A^{*}

A_{1}

D_{2}

D^{*}

egy síkban van,

A^{*} A_{1} = a \sqrt[]{2}

, így

D^{*} D_{2} = a / \sqrt[]{2}

.
Az

A D D^{*} A^{*}

és

A D D_{2} A_{1}

derékszögű trapézból

A^{*} D^{*} = a \sqrt[]{5} / 2

A_{1} D_{2} = a \sqrt[]{3} / 2

. Így a ponyva 2‐2 szimmetrikus kúppalást-részének és az

A^{*} D^{*}

B^{*} C^{*}

élekről lefutó trapézok területének összege

\begin{matrix} T_{1} = 2 (\frac{1}{2} \cdot a \cdot \frac{2 π}{3} \cdot a \sqrt[]{2} + \frac{1}{2} \cdot a \cdot \frac{π}{6} \cdot \frac{a}{\sqrt[]{2}} + \frac{a \sqrt[]{2} + a / \sqrt[]{2}}{2} \cdot \frac{a \sqrt[]{3}}{2}) = 3 \sqrt[]{2} (π + \sqrt[]{3}) \cdot \frac{a^{2}}{4} . \end{matrix}

Másrészt a sorban egymáshoz csatlakozó

A_{2} B_{1} B^{*} A^{*}

A^{*} B^{*} C^{*} D^{*}

D^{*} C^{*} C_{2} D_{1}

téglalapok területének összege, majd a ponyva

T

területe:

\begin{matrix} T_{2} = a (a \sqrt[]{2} + a \frac{\sqrt[]{5}}{2} + \frac{a}{\sqrt[]{2}}) = (3 \sqrt[]{2} + \sqrt[]{5}) \cdot \frac{a^{2}}{2}, \\ T = T_{1} + T_{2} = (3 \sqrt[]{2} (2 + \sqrt[]{3} + π) + 2 \sqrt[]{5}) \frac{a^{2}}{4} \approx 8, 41 a^{2} . \end{matrix}

A sátor térfogatának az

A^{*} D^{*} D_{2} A_{1}

trapéz alatti része a fentebbiek szerint

3

oldalú csonkagúla. Így a térfogatból az

A^{*} A D

és

B^{*} B C

síkokon kívül eső részek összege

\begin{matrix} V_{1} = 2 (\frac{a^{2} π}{3} \cdot \frac{a}{3} + \frac{π}{6} {(\frac{a}{2})}^{2} \cdot \frac{1}{3} \cdot \frac{a}{2} + \frac{1}{3} (\frac{a^{2}}{2} + \frac{a^{2}}{8} + \frac{a^{2}}{4}) \cdot \frac{a \sqrt[]{3}}{2}) = (17 π + 21 \sqrt[]{3}) \cdot \frac{a^{3}}{72}, \end{matrix}

a két sík közti hasábok térfogatának összege

\begin{matrix} V_{2} = a (\frac{a^{2}}{2} + \frac{3 a^{2}}{4} + \frac{a^{2}}{8}) = \frac{11 a^{3}}{8}, \end{matrix}

és így a sátor térfogata

\begin{matrix} V = (99 + 21 \sqrt[]{3} + 17 π) \cdot \frac{a^{3}}{72} \approx 2, 62 a^{3} . \end{matrix}

Végül az alapterület, a részeket a fenti két számítás rendjében felsorolva

\begin{matrix} t = 2 (\frac{a^{2} π}{3} + \frac{a^{2} π}{6 \cdot 4} + \frac{1}{2} \cdot \frac{3 a}{2} \cdot \frac{a \sqrt[]{3}}{2}) + a \frac{5 a}{2} = \frac{a^{2}}{4} (3 (π + \sqrt[]{3}) + 10) \approx 6, 16 a^{2}, \end{matrix}

ennélfogva az átlagmagasság

\begin{matrix} m = \frac{V}{t} = \frac{99 + 21 \sqrt[]{3} + 17 π}{10 + 3 \sqrt[]{3} + 3 π} \cdot \frac{a}{18} \approx 0, 426 a . \end{matrix}

a = 15

m adat behelyettesítésével

T = 1892 m^{2}

V = 8850 m^{3}

t = 1385 m^{2}

m = 6, 40 m

II. A ponyva kiterítési tervéhez (2. ábra) a fent megállapított méreteket csak a kúppalást-részek középponti szögével kell kiegészítenünk.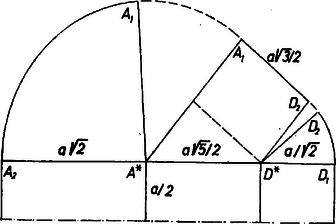

2. ábra

α = ív/sugár

összefüggés alapján az

A^{*}

csúcsnál levő szög

(2 π a / 3) : (\sqrt[]{2} a) = \sqrt[]{2} π / 3 \approx 1, 481 radián = 84, 9^{\circ}

, a

D^{*}

-nál levő pedig ennek fele,

42, 4^{\circ}

Sugár László (Budapest, I. István g. IV. o. t.)
Körmendi Sándor (Szombathely, Latinka S. Gépip. T. IV. o. t.)