Kezdőlap


Feladat:	1511. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Eteli F. , Fuggerth E. , Gegesy F. , Hegedűs A. , Herboly M. , Jobbágy T. , Joó I. , Katona V. , Kocsis F. , Lakatos L. , Losonci Z. , Mészáros J. , Missura Éva , Prémy G. , Printz J. , Rácz Éva , Scháb Margit , Sugár L. , Takács L. , Zambó Péter , Zsolt G.
Füzet:	1968/január, 6 - 8. oldal		PDF \| MathML
Témakör(ök):	Térelemek és részeik, Feladat, Síkgeometriai számítások trigonometriával
Hivatkozás(ok):	Feladatok: 1967/január: 1511. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. I. Legyen a falsík alapéle $A D = a$ , függőleges élei $A B$ , $D C$ , az észlelési helyek $E_{i}$ ‐ ahol $i = 1, 2$ ‐, innen $A D$ , $B C$ látószöge 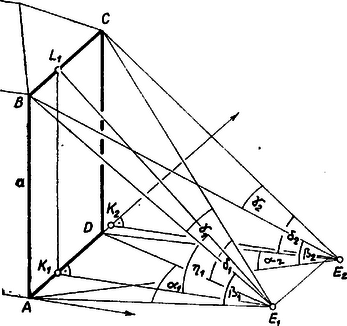$α_{i}$ , ill. $γ_{i}$ .

Mivel

E_{i}

az alapél síkjában van,

E_{i} B A

és

E_{i} C D

derékszögű háromszög, továbbá

A B = D C = a

, ezért

\begin{matrix} A E_{i} = a cotg β_{i}, D E_{i} = a cotg δ_{i}; B E_{i} = \frac{a}{sin β_{i}}, C E_{i} = \frac{a}{sin δ_{i}} . \end{matrix}

(Egyszerűség kedvéért az

i

indexet egyelőre nem írjuk ki.) Az

A D E

, ill.

B C E

háromszögből a koszinusz‐tétellel

\begin{matrix} cos α = \frac{A E^{2} + D E^{2} - A D^{2}}{2 \cdot A E \cdot D E} = \frac{{cotg}^{2} β + {cotg}^{2} δ - 1}{2 cotg β cotg δ}, & (1) \\ cos γ = \frac{\frac{1}{sin^{2} β} + \frac{1}{sin^{2} δ} - 1}{\frac{2}{sin β sin δ}} = \frac{sin^{2} β + sin^{2} δ - sin^{2} β sin^{2} δ}{2 sin β sin δ} . & (2) \end{matrix}

II. Legyen az

A D

egyenesnek

E_{i}

-hez legközelebbi pontja

K_{i}

B C

-é pedig

L_{i}

. Ezeket az

E

-n átmenő és az élre merőleges sík metszi ki,

A D ∥ B C

miatt mindkettőt ugyanaz a függőleges sík, így elég

K

-t meghatároznunk. A függvény értelme és a koszinusz-tétel alapján

\begin{matrix} A K = A E \cdot cos E A D ∢ = \frac{A E^{2} + A D^{2} - E D^{2}}{2 A D} = & (3) \\ = \frac{α}{2} ({cotg}^{2} β - {cotg}^{2} δ + 1), \end{matrix}

másrészt az

A D E

háromszög

t

területe két kifejezésének egyenlőségéből

\begin{matrix} K E = \frac{2 t}{A D} = \frac{E A \cdot E D sin α}{A D} = a cotg β cotg δ sin α . \end{matrix}

(4)

Így

K L

-nek

η

látószögére

\begin{matrix} cotg η = \frac{E K}{K L} = cotg β cotg δ sin α . \end{matrix}

(5)

(3) és (5) azonban csak akkor ad választ a feladat kérdésére, ha

K

A D

élszakaszon adódik:

0 ≦ A K ≦ A D

. Különben,

A K < 0

esetén

A

A K > A D

esetén pedig

D

A D

élszakasznak

E

-hez legközelebbi pontja, a

B C

élszakaszon megfelelően

B

, ill.

C

, végül az emelkedési szög

β

, ill.

δ

.
III.

A K_{i}

K_{i} E_{i}

az észlelési pont koordinátái abban a derékszögű koordináta‐rendszerben, melynek origója

A

, abszcisszatengelyének pozitív fele az

A D

félegyenes és az ordináták az

E_{i}

-t tartalmazó félsíkon pozitívok. Így az

E_{1} E_{2}

távolság a koordináta‐geometria távolságképletével állapítható meg.
IV. A numerikus adatokkal az

E_{1}

észlelőhelyre

α_{1} = 47, 6^{\circ}

γ_{1} = 36, 6^{\circ}

A K_{1} = 7, 83 m

K_{1} E_{1} = 22, 52 m

η_{1} = 41, 6^{\circ}

; az

E_{2}

észlelőhelyre

α_{2} = 38, 6^{\circ}

γ_{2} = 32, 0^{\circ}

A K_{2} = 21, 39 m

(> A D)

K_{2} E_{2} = 23, 80 m

, a felső él

E_{2}

-höz legközelebbi pontja

C

, emelkedési szöge

40^{\circ}

. Végül a koordinátákból

E_{1} E_{2} = 13, 62 m

.
Zambó Péter (Miskolc, Földes F. g. II. o. t.)

Megjegyzés. Az

E_{1} E_{2}

távolság az

A E_{1} E_{2}

(vagy

D E_{1} E_{2}

) háromszögből is számítható, az

E_{i} A D

(ill.

E_{i} D A

) szögek előzetes kiszámítása alapján.