Kezdőlap


Feladat:	1510. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Fischer Ágnes , Göndőcs Ferenc , Horváth Sándor
Füzet:	1968/január, 4 - 6. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Szinusztétel alkalmazása, Síkgeometriai bizonyítások, Feladat
Hivatkozás(ok):	Feladatok: 1967/január: 1510. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Az ábra háromszögeiben szereplő közös, ill. egyenlő oldalak és közös, ill. egyenlő szögek reményt nyújtanak arra, hogy az összefüggésekben felhasznált fölösleges alkotórészek kiküszöbölésével célhoz érünk. ‐ Az állítás értelmét veszti, ha a kör átmegy $A$ -n, ezért ezt az esetet kizárjuk. Ekkor $A$ , $D$ , $E$ különböző pontok és az $A D E$ háromszög hasonló az $A C B$ háromszöghöz, mert szögeik páronként egyenlők, hiszen az $A B$ , $A C$ egyenespár a körnek két szelője. Legyen $A B C ∢ = A E D ∢ = β$ , $A C B ∢ = A D E ∢ = γ$ , továbbá $F A B ∢ = α_{1}$ , $F A C ∢ = α_{2}$ , az utóbbiak rendre azonosak vagy csúcsszögek a $G A B$ , ill. $G A C$ szöggel aszerint, hogy $A$ a körre nézve külső, ill. belső pont.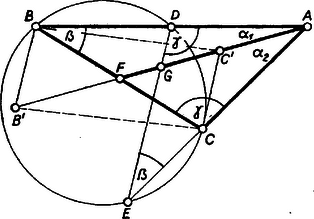

1. ábra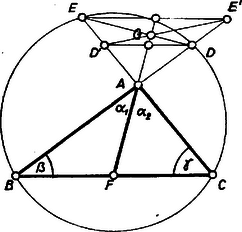

2. ábra

Fejezzük ki

G D

-t,

G E

-t a színusz‐tétel alapján az

A G D

, ill.

A G E

háromszögből és alakítsuk arányukat az alábbiak szerint:

\begin{matrix} G D : G E & = \frac{G A sin α_{1}}{sin γ} : \frac{G A sin α_{2}}{sin β} = \frac{sin β}{sin γ} : \frac{sin α_{2}}{sin α_{1}} = & (2) \\ = \frac{A C}{A B} : \frac{sin α_{2}}{sin α_{1}} . \end{matrix}

(Az arány tagjait szoroztuk

sin β / G A sin α_{1}

-gyel, majd a színusz tételt alkalmaztuk az

A B C

háromszögre.) Hasonlóan az

A F B

és

A F C

, majd ismét az

A B C

háromszög alapján

\begin{matrix} F B : F C & = \frac{F A sin α_{1}}{sin β} : \frac{F A sin α_{2}}{sin γ} = \frac{sin γ}{sin β} : \frac{sin α_{2}}{sin α_{1}} = \\ = \frac{A B}{A C} : \frac{sin α_{2}}{sin α_{1}} . \end{matrix}

Mivel pedig

F B = F C

, azért

\begin{matrix} \frac{sin α_{2}}{sin α_{1}} = \frac{A B}{A C} . \end{matrix}

Ezt (2) utolsó arányába helyettesítve és az arány tagjait egyaránt

A B \cdot A C

-vel szorozva az (1) állítást kapjuk.
Bizonyításunk akkor is érvényes, ha a kör érinti p1. az

A B

egyenest, és így

D

helyén is

B

értendő, sőt akkor is, ha ugyanígy még

E

is egybeesik

C

-vel. Az utóbbi esetben azonban az állítás nyilvánvaló, mert az

A B C

háromszög egyenlő szárú, másrészt

G

azonos

F

-fel.

Horváth Sándor (Budapest, I. István g. III. o. t.)

II. megoldás. Húzzunk párhuzamost

D E

-vel

B

-n és

C

-n át, és messék ezek

A F

-et a

B'

, íll.

C'

pontban. Ekkor a

G D A

B' B A

, a

G E A

C' C A

, valamint az

A D E

A C B

hasonló háromszög‐párokból

\begin{matrix} G D : G E = \frac{A D}{A B} \cdot B B' : \frac{A E}{A C} \cdot C C' = \frac{A D}{A E} : \frac{A B}{A C} = \frac{A C}{A B} : \frac{A B}{A C} = A C^{2} : A B^{2}, \end{matrix}

ugyanis

B B' C C'

paralelogramma, és így

B B' = C C'

Fischer Ágnes (Budapest, Móricz Zs. g. I. o. t.)

III. megoldás. Húzzunk párhuzamost

B C

-vel

D

-n és

E

-n át, és messe ez

A C

-t

D'

-ben, ill.

A B

-t

E'

-ben. Ekkor

A F

nyilvánvalóan felezi

D D'

-t és

E E'

-t, a

D D' E E'

trapéz két párhuzamos oldalát, ezért átmegy az átlók metszéspontján is. A

D E

átló

G

-ben metszi

A F

-et, így

G

-n átmegy

D' E'

is. Hasonló háromszögekből

\begin{matrix} \frac{G D}{G E} = \frac{D D'}{E E'} = \frac{A D'}{A E} . \end{matrix}

A D E

A C B

és

A D' D

háromszögek hasonlók, ebből

\begin{matrix} \frac{A D}{A E} = \frac{A C}{A B}, \frac{A D'}{A D} = \frac{A C}{A B} \end{matrix}

és ezek összeszorzásával

\begin{matrix} \frac{G D}{G E} = \frac{A D'}{A E} = \frac{A C^{2}}{A B^{2}} . \end{matrix}

Göndőcs Ferenc (Kapuvár, II. sz. Ált. Isk., 8. o.t.)