Kezdőlap


Feladat:	1509. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Szenes Katalin , Takács László
Füzet:	1968/október, 51 - 52. oldal		PDF \| MathML
Témakör(ök):	Beírt kör, Hozzáírt körök, Feladat
Hivatkozás(ok):	Feladatok: 1967/január: 1509. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

a) A szögfelező átmegy a beírt kör $O$ középpontján és merőleges $B' C'$ -re ezért elég azt belátnunk, hogy $B B^{*}$ is, $C C^{*}$ is merőleges $A O$ -ra.
Ha $A'$ rajta van $A O$ -n, akkor a háromszög egyenlő szárú: $A B = A C$ , $A O$ a szimmetriatengely, és $B^{*}$ , $C^{*}$ azonos $A'$ -vel, $B B^{*}$ és $C C^{*}$ azonos a $B C$ egyenessel.

A B \neq A C

esetén válasszuk a betűzést úgy, hogy

A B < A C

legyen, ekkor

A'

A O

-nak

C'

-t tartalmazó partján van, ezért

C^{*}

a háromszögön kívül adódik,

B^{*}

viszont a belsejében.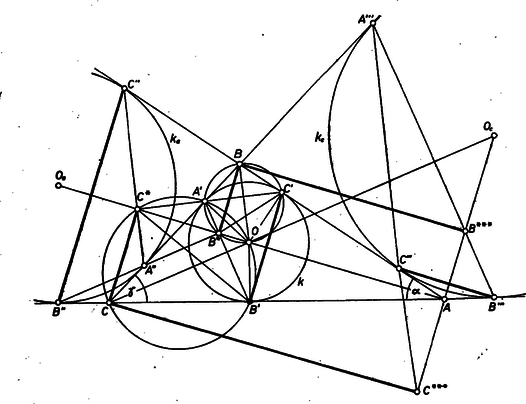

O B^{*}

szakaszt

A'

-ből és

C'

-ből egyenlő szögben látjuk, ugyanis a szimmetria és az

O A' B'

háromszög egyenlő szárú volta miatt

\begin{matrix} O C' B^{*} ∢ = O B' B^{*} ∢ = O A' B^{*} ∢, \end{matrix}

eszerint

A'

C'

O

és

B^{*}

egy kör pontjai. Másrészt az első három ponton átmenő, egyértelműen meghatározott kör átmegy

B

-n is, mert

O A' B

és

O C' B

derékszögek, s így az

O A' B C'

deltoid húrnégyszög, és e körben

O B

átmérő. Ezért a

B B^{*} O ∢

derékszög, s ezt akartuk bizonyítani.
A

C C^{*} O ∢

derékszög voltát lényegében ugyanígy bizonyítjuk, de figyelembe véve, hogy

A O

, azaz

O C^{*}

szétválasztja

A'

-t és

B'

-t. Az

O A' C^{*} B'

négyszög

A'

-nél levő külső szögére:

\begin{matrix} O A' C' ∢ = O C' A' ∢ = O C' C^{*} ∢ = O B' C^{*} ∢, \end{matrix}

tehát a négyszög húrnégyszög, másrészt körülírt köre

O

A'

B'

miatt átmegy

C

-n, ezért

C C^{*} O ∢ = C A' O ∢

, derékszög.

b) Tekintsük az

A B C

háromszögnek azt a

k_{a}

külső érintő körét, amely a

B C

oldalt a háromszöget nem tartalmazó partján, az

A''

pontban érinti, középpontja legyen

O_{a}

. Legyen az

A C

A B

félegyenesen levő érintési pontja

B''

C''

és messe az

A O_{a}

egyenest

A'' B''

B^{* *}

pontban,

A'' C''

C^{* *}

-ban. Érvényes a feladat állításának megfelelője:

B'' C'' ∥ B B^{* *} ∥ C C^{* *}

, és ez a fentiekhez hasonlóan bizonyítható. S mivel eszerint pl.

B^{* *}

is,

B^{*}

is a

B

csúcs vetülete az

A

-ból induló belső szögfelezőn, e két pont azonos. (Az is fennáll, hogy

B^{*}

-ban

A' B'

és

A'' B''

merőlegesen metszi egymást, hiszen merőlegesek a

C

-beli belső, ill. külső szögfelezőre.)

c) Legyen végül az

A B

oldalt kívülről érintő

k_{c}

, kör középpontja

O_{c}

, érintési pontja a

B C

C A

A B

egyenesen rendre

A'''

B'''

C'''

, továbbá

A''' B'''

-nek és

A''' C'''

-nek az

A O_{c}

külső szögfelezőn levő metszéspontja

B^{* * *}

, ill.

C^{* * *}

, ekkor hasonlóan bizonyítható, hogy

B''' C''' ∥ B B^{* * *} ∥ C C^{* * *}

Szenes Katalin (Budapest, I. István Gimnázium)
Takács László (Sopron, Széchenyi I. Gimnázium)

Megjegyzés. Az állítás háromszögek hasonlósága alapján is bizonyítható, ezt

B^{*}

-ra vonatkozóan vázoljuk, a szokásos jelöléseket használjuk.

C A' B'

egyenlő szárú háromszög, ezért

A B' B^{*} ∢ = 90^{\circ} + γ / 2

B' A B^{*} ∢ = α / 2

, így

A B^{*} B' ∢ = β / 2 = A B O ∢

, tehát

A B^{*} B' ▵ \sim A B O ▵

. Innen

\begin{matrix} \frac{A B^{*}}{A B} = \frac{A B'}{A O}, \end{matrix}

emiatt az

A

-nál egyenlő szöggel bíró

A B^{*} B

és

A B' O

háromszögek is hasonlók, az utóbbiban

B'

-nél derékszög van, tehát az

A B^{*} B ∢

is derékszög.