Kezdőlap


Feladat:	1507. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bajmóczy E. , Battha L. , Berács J. , Berkes Z. , Bulkai T. , Csörgei J. , Csörgő Piroska , Draschitz R. , Döme Éva , Fiala T. , Gegesy F. , Hunyadvári L. , Juhász Ágnes , Kas Péter , Kocsis F. , Koren A. , Külvári I. , Lublóy L. , Mérő L. , Moson P. , Munk S. , Orbán G. , Pap Márta , Perémy G. , Pintz J. , Rácz Éva , Sergyán Stefánia , Somos E. , Sugár L. , Szenes Katalin , Szűcs A. , Takács L. , Tóth Tibor , Varsányi Anikó , Vass Erzsébet , Végvári L. , Vetier A.
Füzet:	1967/november, 126 - 128. oldal		PDF \| MathML
Témakör(ök):	Egyenlőtlenségek, Függvényvizsgálat, Feladat
Hivatkozás(ok):	Feladatok: 1967/január: 1507. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

(2) bal és jobb oldala különbségének, valamint a (3) és (4) két oldalán álló különbségeknek közös alakja

\begin{matrix} f (u) - f (v) = \frac{p u + q}{r u + s} - \frac{p v + q}{r v + s} = \frac{(r q - p s) (v - u)}{(r u + s) (r v + s)} = \frac{(r q - p s) (v - u)}{r^{2} (u + \frac{s}{r}) (v + \frac{s}{r})} \end{matrix}

(5)

(ugyanis I.-nek és II.-nek csak

r \neq 0

esetén van értelme).
(I) nevezője

\begin{matrix} r x + s = r (x + \frac{s}{r}), \end{matrix}

zárójelbeli tényezője az I.-ben és II. -ben szereplő

- s / r

helyen eltűnik, előtte negatív, utána pozitív. S mivel

i = 1, 2

értéke mellett

\begin{matrix} az I. esetben x_{i} - ε < x_{i} < - s / r, a II. esetben - s / r < x_{i} < x_{i} + ε, \end{matrix}

azért (5) nevezőjében a két zárójelbeli tényező mindegyik

u

v

számpárunk esetében egyenlő előjelű, tehát szorzatuk mindig pozitív. Ugyanez áll (5) számlálójára is ‐ ennélfogva (5) mindig pozitív ‐, ugyanis a feltevés folytán

r q - p s > 0

, továbbá mindig

v - u > 0

, hiszen (2) esetében

u = x_{1}

v = x_{2}

, és mindig áll

x_{2} - x_{1} > 0,

(3) és (4) esetében pedig mindig

v - u = ε

. ‐ Ezzel (2)-t máris bebizonyítottuk.
(3) és (4) bizonyításához ‐ mivel két oldaluk (5) szerinti átalakításában a számláló közös és pozitív ‐ csak a nevezők változó része közti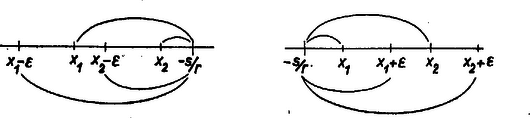

\begin{matrix} (x_{1} - ε + \frac{s}{r}) (x_{1} + \frac{s}{r}) > (x_{2} - ε + \frac{s}{r}) (x_{2} + \frac{s}{r}), & (3a) \\ (x_{1} + \frac{s}{r}) (x_{1} + ε + \frac{s}{r}) < (x_{2} + \frac{s}{r}) (x_{2} + ε + \frac{s}{r}) & (4a) \end{matrix}

egyenlőtlenséget kell belátnunk. Ezek abból adódnak, hogy a tényezők abszolút értéke rendre a számvonal

x_{1} - ε

x_{1}

x_{2} - ε

x_{2}

, ill.

x_{1}

x_{1} + ε

x_{2}

x_{2} + ε

abszcisszájú pontja és minden esetben a

- s / r

pont közti távolság, és a feltevések folytán az I. esetben a (

3 a

) bal oldalán, a II. esetben pedig a (

4 a

) jobb oldalán álló 2‐2 távolság rendre nagyobb, mint a másik oldalon álló megfelelő távolság (1. ábra). ‐ Ezzel a bizonyítást befejeztük.

1. ábra

Kas Péter (Budapest, Szinyei Merse P. g. IV. o. t.)
Pap Márta (Budapest, Kölcsey F. g. III. o. t.)

Megjegyzés. Szemléljük a bebizonyított állításokat a

p = s = 0

q = r = 1

eset példáján, a jól ismert

f (x) = 1 / x

függvényen. Ekkor (2) szerint (1) az

x < 0

és

x > 0

értelmezési tartomány mindkét összefüggő részében külön-külön csökkenő.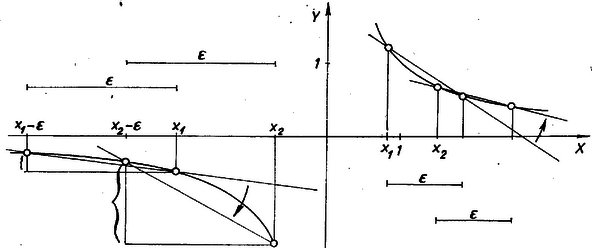

2. ábra

(3) és (4) e részek két-két egyenlő, ti.

ε

hosszúságú intervallumában bekövetkezett csökkenéseket hasonlítják össze, mindig a nagyobb függvényértékekből a kisebbet vonva ki. Az I. esetben

x_{2}

, a II.-ban

x_{1}

van közelebb az

x = 0

szakadási helyhez, és (3) és (4) azt fejezi ki, hogy a mondott csökkenés a szakadási helyhez közelebb eső

ε

-intervallumban nagyobb.
(3)-at és (4)-et

ε

-nal osztva az egyenlőtlenségek iránya változatlan marad, és azt kapjuk, hogy a görbe egyenlő vetületű húrjainak meredeksége csökken, míg a szakadási helyhez balról közeledünk, és nő, miután e helyet átléptük.