| Feladat: | 1501. matematika feladat | Korcsoport: 16-17 | Nehézségi fok: nehéz |
| Megoldó(k): | Balogh József , Bodor István , Bottyán István , Csörgei József , Fuggerth Endre , Göndőcs Ferenc , Herboly Miklós , Hunyadvári László , Joó István , Kocsis Ferenc , Lakatos László , Lempert László , Moson Péter , Nádai László , Perémy Gábor , Pintz János , Siklósi István , Somos Endre , Szabó Klára , Takács László , Tátray Péter , Varga Gabriella , Verdes Sándor , Vetier András , Zöldy Béla | ||
| Füzet: | 1969/január, 4 - 7. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Diszkusszió, Háromszögek szerkesztése, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1966/december: 1501. matematika feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás. I. Legyen az előírásoknak megfelelő háromszögben az oldal, a -ből kiinduló belső szögfelezőnek az egyenesig terjedő szakasza, valamint a és oldalak összege rendre egyenlő az adott , és szakasszal. 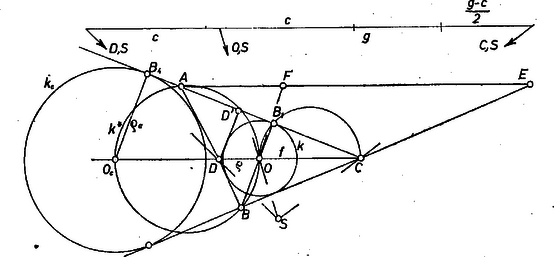 1. ábra Az szög belső szögfelezője -t -ban metszi, -n levő pontja legyen . Ekkor az előzők és a szögfelező osztásaránya alapján
A kapott háromszögben felezi az szöget, másrészt az oldalak hosszára vonatkozóan (1), ill. (2) alapján ezekből pedig egyszerű számítás szerint és . A szerkesztés végrehajtásának nyilvánvaló első föltétele . A pont létrejön és valódi kör, ha ; továbbá -ből lehet érintőt húzni a kapott -hoz, ha , azaz II. A -ből húzott külső szögfelező akkor és csak akkor metszi az egyenest egy pontban, ha a . Legyen ekkor és , így a oldal -n túli meghosszabbításán van és a szakaszon van rajta a háromszög oldalához hozzáírt külső érintő kör középpontja. A háromszög a , és adatokból a fentiekhez hasonlóan szerkeszthető. Fordítsuk rá -t körül a félegyenes szakaszába, és messük a (belső) szögfelezővel az szakaszt -ban (2. ábra). 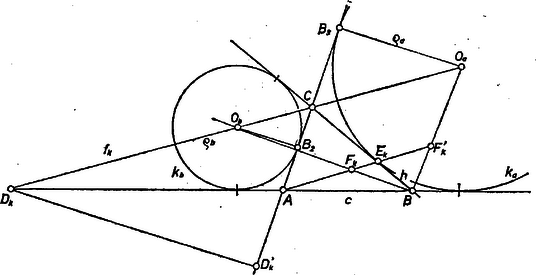 2. ábra Így és , továbbá
A szerkesztés helyessége a fentihez hasonló számítással bizonyítható. A szerkesztés végrehajtható, ha és . Az utóbbi teljesülése esetén (3) és alapján Göndőcs Ferenc (Győr, Révai M. Gimn.) dolgozatából, kiegészítéssel Megjegyzések. 1. A II. adathármas esetében célhoz érünk a oldalhoz hozzáírt külső érintő kör fölhasználásával is. Ennek középpontja a szakasz -n túli meghosszabbításán és az szög külső szögfelezőjén van, és , másrészt a kör -n levő érintési pontjára . 2. Hasonlóan az I. adathármas esetében az oldalhoz hozzáírt kör ( meghosszabbításán levő) középpontjára és -n levő érintési pontjára és , ezek alapján a fentiekhez hasonlóan végezhetjük a szerkesztést. 3. Megoldhatjuk a feladatot úgy is, hogy a háromszög oldalegyeneseit érintő körök és , ill. , középpontjai közül az előbbi, ill. az utóbbi párt egyidejűen használjuk fel. Ezt csak az I. adathármas esetére mutatjuk be. Az aránypárból fölcseréléssel, majd az 1. ábra és hasonló háromszögei alapján Siklósi István (Budapest, Berzsenyi D. Gimn.) 4. A fenti , körpárnak a külső, pedig a belső hasonlósági pontja (mert centrálisukat az közös belső érintő -ben metszi), így
Ezek alapján a csúcs és a félegyenes helyzetét felvéve, ezen és , továbbá, (4) alapján kijelölhető. Ekkor a -ben -ra emelt merőlegesből a körüli, sugarú körívvel kimetszhetjük -t, -nak -re való tükörképe a egyenes, alapján megkaphatjuk -t és -t (vagy alapján -t és -t), és ennek -ből húzott érintője az oldal egyenese. A bizonyítást és a diszkussziót a fentiekhez hasonlóan végezheti el az olvasó. és esetére -nak -n levő vetületére hasonlóan . II. megoldás (vázlat). Alapszerkesztésre vezethetjük vissza feladatunk mindkét részét az 1438. feladatban1 bebizonyított ‐ ill. csak kimondott ‐ tétel felhasználásával. Eszerint a középpontú, sugarú (ill. a -val és -val meghatározott) körhöz tetszés szerinti pontjában húzott érintőre fölmérjük szakaszt, majd ennek (ill. ) végpontja körüli (ill. ) sugarú körrel metsszük az előbbi kört -ben. Ekkor , (ill. ), tehát ismerjük a keresett háromszög -beli szögét, innen kiinduló oldalainak összegét (különbségét) és a szemben fekvő oldalt (3. ábra). 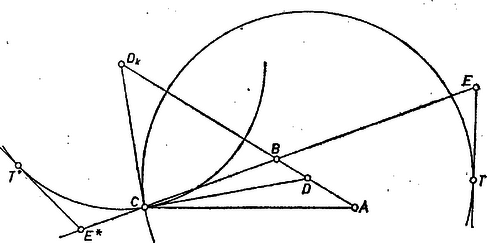 1. ábra Lakatos László (Budapest, Százados úti Gimn.) 1K. M. L. 33 (1966) 208. o. (a mostani feladat kitűzését tartalmazó számban): Az háromszög -ből kiinduló szögfelezőjének az oldallal való metszéspontja körül sugárral kört írunk, másrészt a oldalt -n túl meghosszabbítjuk a szakasszal. Bizonyítandó, hogy ekkor az -ből a körhöz húzott érintő hossza egyenlő -vel. Hasonlóan a -nél levő külső szög felezőjének -n levő pontja körüli, sugarú körhöz a -től felé fölmért szakasz végpontjából húzott érintő hossza szintén . |