Feladat: 1496. matematika feladat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Balogh J. ,  Berács J. ,  Bottyán I. ,  Bulkai T. ,  Dajka Marianne ,  Dombi J. ,  Lublóy L. ,  Nagy Elemér ,  Perémy G. ,  Pintz J. ,  Takács L. ,  Tátrai P. ,  Tiszai I. ,  Vályi István ,  Vetier A. ,  Wagner A. 
Füzet: 1967/szeptember, 15 - 16. oldal  PDF  |  MathML 
Témakör(ök): Térfogat, Szabályos sokszögek által határolt testek, Feladat
Hivatkozás(ok):Feladatok: 1966/november: 1496. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Az adott lapokkal határolt testet többféleképpen készíthetjük el, tekintsük először a következőt. Legyenek az ABCD és ABEF négyzetlapok egy H szabályos háromoldalú hasáb oldallapjai (1. a és b ábra). Négy háromszöglapból elkészítjük egy G főcsúcsú N szabályos négyoldalú gúla nyitott palástját, és ezt ráillesztjük H-nak CDFE négyzetlapjára, további három háromszögből egy K főcsúcsú T szabályos tetraéder palástját, és ezt H-nak ADF fedőlapjára illesztjük, végül nyolcadik háromszöglapként H-nak BCE alaplapját vesszük.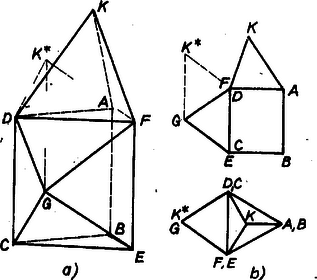

 
 
1. ábra
 

H, N, T térfogata ismert módon egyszerűen számítható, így a test térfogata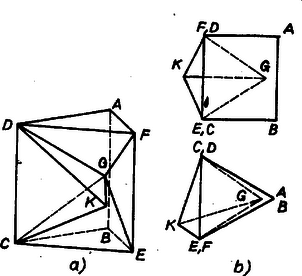
V=34+26+212=3+24≈0,786...
térfogategység; kisebb az 1464. feladatban vizsgált, ugyanezen lapok együttesével határolt test 0,956... egységnyi térfogatánál.
 
II. A HN testkombináció szimmetrikus az AB él felező merőleges síkjára ‐ valamint az ABG síkra is ‐, ezért a fentivel egybevágó testet kapunk, ha T-t az alaplapra illesztjük (kifelé). N oldallapjaira kifelé nem illeszthetjük rá T-t, mert úgy N és T két-két, az illeszkedési lappal szomszédos lapja egy-egy síkba esnék, együtt egy-egy rombuszlapot adna. Ugyanis G-ből CD-vel és EF-fel párhuzamos és egyenlő GK* szakaszt húzva CDK*G és EFK*G rombusz, így K*D és K*F is a közös élhosszúsággal egyenlő, tehát DFGK* szabályos tetraéder, márpedig a DFG lapra kifelé csak egyféleképpen lehet tetraédert illeszteni.
 
III. V-nél kisebb térfogatú testet is határolhatunk az adott lapokkal, ugyanis akár T-t, akár N-et H megfelelő lapjára befelé is ráállíthatjuk ‐ a gúlát mintegy kivájva H-ból. Mindkettőt egyidejűen azonban nem fordíthatjuk befelé, mert úgy bizonyos lapjaik átmetszenék egymást, a hurkolt sokszögekre emlékeztető térbeli alakzatot kapnánk, és azokra nem értelmezhetnők a térfogatot. Könnyen belátható, hogy ‐ a mondott szimmetriák miatt ‐ T-t befelé a HN kombinációnak 3 lapjára állítva kapunk különböző testeket, pl. az ADF, FDG és a CDG lapra. Ha pedig N-et fordítjuk befelé, akkor ugyanerre a 3 lapra állíthatjuk T-t kifelé. Az utóbbi 2 esetben ami a kivájt HN-re nézve ,,kifelé'', az önmagában N-re nézve ,,befelé''.
 
 
2. ábra
 


A 2. ábra a befelé illesztett N-nek CDG lapjára állított T esetét mutatja; mindkét b) ábra két vetületben mutatja az a) ábra testjét a képsíktengely és a vessző-jelölések elhagyásával.
Az ilyen testek esetében T, ill. N térfogata kivonandó a másik két elem térfogatának összegéből.
Vályi István (Budapest, Fazekas M. gyak. g. III. o. t.)
 

Megjegyzések. 1. A feladat nem kívánta az összes lehetséges testek előállítását. Némely dolgozat azonban rámutatott a többféle lehetőségre, majd kiválasztotta az 1. ábrabelit, mondván, hogy csak a konvex esetre szorítkozik. Emiatt jegyezzük meg, hogy ‐ amint az 1. b) ábra elölnézeti képéből jól látható ‐ ez a test sem konvex.
2. Néhány dolgozat úgy vélte megoldani a feladatot, hogy egy szabályos oktaéder papírmodelljét 3 él mentén szétvágta két négyoldalú gúla palástjává (vagyis egy éle és az ennek végpontjaiba befutó, rá merőleges élek mentén), majd a négyzetlapokkal lezárta e gúlákat. Ez ‐ bár a két gúla a közös élükön még összefügg ‐, mégis mesterkélt megoldás. Mások e két gúlát egymáshoz rögzítették egy szabályos tetraéder közéjük iktatásával. Ekkor azonban, a tetraéder és gúlalapok már látott esetén felül az alapnégyzetek is egy síkba esnek; a testet 1 téglalap, 2 trapéz és 2 háromszög határolja; ezt már nem fogadtuk el megoldásnak.