Feladat: 1495. matematika feladat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Langer Tamás ,  Szűcs András 
Füzet: 1967/november, 120 - 122. oldal  PDF  |  MathML 
Témakör(ök): Teljesgráfok, Euler-gráfok (unikurzalitás), Szabályos sokszögek geometriája, Feladat
Hivatkozás(ok):Feladatok: 1966/november: 1495. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Megadunk egy előírást a bejárásra, mégpedig olyant, amelynél minden útszakaszon (oldalon vagy átlón) megszakítás nélkül haladunk végig, irányt csak a sokszög csúcsaiban változtatunk.
Jelöljük a sokszög csúcsait (tetszés szerinti sorrendben) a 0,1,2,..., 2n-1, 2n számokkal. A 0-ból indulunk el, az 1-en, 2-n át visszatérünk oda, majd minden lépésben 2 újabb csúcsot az előbbiekkel és egymással összekötő útszakaszokat járjuk be. Ha a 0,1,...,2k (k<n) közti útszakaszokat már bejártuk és visszatértünk 0-ba, akkor a következő úton megyünk tovább:

0,2k+1,1,2k+2,2,2k+1,3,...,2k-1,2k+2,2k,2k+1,2k+2,0.
Ezzel programunkat megvalósítottuk és visszaértünk a 0-ba, az eljárást tovább folytathatjuk, míg minden útszakaszt be nem jártunk.
 
 
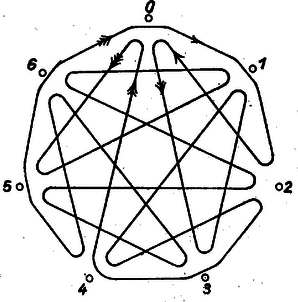1. ábra
 

Az 1. ábra a szabályos 7-szög ilyen bejárását mutatja be. Megjegyezzük, hogy a sokszög szabályos voltát nem használtuk fel, legfeljebb, amennyiben csak egyenes útszakaszokat engedünk meg, csak annyit, hogy 2n+1 pont van adva, amelyek közül nincs 3 egy egyenesen.
 
Langer Tamás (Budapest, Apáczai Csere J. gyak. g. IV. o. t.)

 
II. megoldás. A bejárás lehetőségét konkrét bejárási előírás megadása nélkül fogjuk belátni. Egy A csúcsból tetszés szerint elindulva haladjunk tovább minden csúcsból valamilyen útszakaszon, amíg olyan csúcsba nem érünk, amelyikből induló minden útszakaszon jártunk már; röviden: amíg megakadunk. Ez csak az A csúcsban lehet. Ugyanis minden más csúcson mindig át tudunk haladni, mert egy áthaladás 2 ott végződő útszakaszt használ fel, így a csúcsban az egymás utáni áthaladások után bejáratlanul maradt útszakaszok száma a páros számok 2n-2, 2n-4,... sorozatán át csökken. A-ban viszont a páratlan számok sorozatán át csökken ez a szám, mert az elindulás után 2n-1 útszakaszt hagytunk vissza.
Amennyiben az A-beli megakadásig nem jártuk be az egész úthálózatot, akkor javítjuk útvonalunkat úgy, hogy több útszakaszon haladjon át. Mindenesetre minden csúcson legalább egyszer áthaladtunk, hiszen bejártuk az A-ból odavezető utat. Minden olyan csúcsban, ahová még fut be bejáratlan útszakasz, páros az ilyenek száma. Egy ilyen B csúcsból indulva és a maradék hálózaton megtett utunkat egy más színnel rajzolva csak B-ben akadhatunk meg ismét. Mármost a két különböző színű útvonalat eggyé tehetjük úgy, hogy az első bejárás során B-be érkezve beiktatjuk az új színnel bejárt útvonalat, s csak ezután haladunk tovább az első útvonalon.
Ha még mindig nem jártuk be az egész hálózatot, akkor ismét olyan részhálózat maradt vissza, mint az első megakadás után, s így megismételhetjük eljárásunkat. Az eredeti sokszög oldalainak és átlóinak száma véges, ezért véges számú hasonló útvonal-módosítás után egyetlen, az egész hálózatot bejáró útvonalat kapunk.
 
Megjegyzések 1. Feladatunk állítása egy gráfelméleti tételből is következik. *
2. Megadjuk egy más, érdekes, rendszeres bejárás utasítását. A sokszög egymás utáni csúcsait ismét a 0,1,2,...,2n számokkal jelöljük. Előkészítésül az átlókat osztályokba soroljuk, r-edosztályúnak nevezzük azokat, amelyekkel a sokszöget kettévágva a kisebbik rész r oldalt tartalmaz a kerületből. Így a legnagyobb osztályszám n; az oldalakat első osztályú átlóknak tekintjük, ekkor az osztályok száma n. Továbbá minden átlón előre megállapítjuk a menetirányt: úgy haladunk, hogy a sokszög nagyobbik része ‐ más szóval a sokszög középpontja ‐ jobb kezünk felé essék (röviden: az átlókat irányítjuk). Így minden útszakasznak kijelöltük a kezdő és végpontját, minden csúcsban n átló kezdődik (indul), és n átló végződik (érkezik), minden egyes átló-osztályból egy-egy.
A bejárást a következő előírások szerint végezzük: 1. A 0-jelű csúcsból indulunk ki. 2. Ekkor és minden ide való visszaérkezés után a még rendelkezésre álló átlók közül a legmagasabb osztályú átlón haladunk tovább. 3. A 0-tól különböző csúcsba érkezve ugyanolyan osztályú átlón haladunk tovább, mint amilyenen oda érkeztünk. 4. A 01 szakasz bejárása után a 0 csúcs megkülönböztetett szerepét átadjuk az 1 csúcsnak, majd hasonlóan a 2-nek és í. t.
Eljárásunk szemléletesen a következőt jelenti. 0-ból a 0r átlón megindulva végigjárjuk az r,2r,3r,... csúcsokat ‐ ahol a 2n-nél nagyobb számokat a 2n+1-gyel való osztásuk maradékával kell helyettesíteni ‐, míg vissza nem érünk a 0-ba. Ha r-nek és 2n+1-nek nincs 1-nél nagyobb közös osztója, akkor ez az összes r-edosztályú átló alkotta csillag-2n+1-szög * bejárása után következik be (*).
 
 
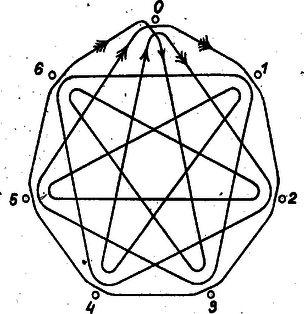2. ábra
 

A 2n+1=7 esetben (2. ábra) r=3 és 2 esete is ilyen, s így 0-ból indulva az összes 3-ad-, majd 2-odosztályú átlót bejárjuk, majd végigmegyünk az oldalakon. Hasonló a helyzet, ha 2n+1 prímszám. 2n+1=15-szögben r=7, 4 és 2 esete ilyen (lásd a csúcsok bejárás szerinti sorrendjének alábbi felsorolását). Az r=n eset mindig ilyen, mert n és 2n+1 relatív prímek.
Ha r és 2n+1 legnagyobb közös osztója d>1, akkor (2n+1)/d=e lépés után jutunk vissza a 0-ba egy (egyszerű vagy csillag-) szabályos e-szög bejárása után (**). Ekkor a többi r-ed osztályú átló d-1 további, az elsővel egybevágó sokszöget ad. Ezeket akkor járjuk be, amikor az 1,2,...,d-1 csúcs veszi át a 0 szerepét. A szabályos 15-szög elveink szerinti bejárásában r=6 esetére 3 csillagötszög, r=3 esetére 3 közönséges ötszög adódik a 0, 1, 2 csúcsokból kiindulva, r=5 esetére pedig hasonlóan 5 szabályos háromszög a 0, 1, 2, 3, 4 csúcsokból kiindulva. A csúcsok alábbi felsorolásában egy-egy ilyen vonalrész bejárásának befejezését, valamint a 15-szög 1‐1 oldalán való áthaladást is, pontosvessző jelzi.
Ezzel lényegében be is bizonyítottuk, hogy a bejárási előírás 3. pontja mindig teljesíthető. Minden jk¯ útszakaszon áthaladtunk ‐ ahol j<k≤j+n (k>2n esetén itt is a mondott helyettesítéssel) ‐, és csak egyszer. Ha ugyanis nem haladtunk át rajta, mielőtt j átveszi a 0 szerepét, akkor a szerepátvétel után sorra vesszük a j-ből kiinduló összes még be nem járt átlót, utoljára pedig a j(j+1)¯ oldalt, és ezzel adjuk át a 0 pont szerepét a (j+1)-nek. ‐ Hátra volna azonban még a (*) és (**) jelű állítások bizonyítása.
 
Szűcs András (Budapest, Fazekas M. gyak. g. III. o. t.)
dolgozata alapján, kiegészítésekkel

3. Ha 2n+1 prímszám, akkor a következő előírás is a fenti útvonalra vezet: 1. A 0n¯ átlón indulunk és 2. minden csúcsból az onnan kiinduló legmagasabb osztályú átlón haladunk tovább. ‐ Ha azonban 2n+1 összetett szám, akkor így a fenti (2n+1)/d oldalú csillagsokszögeket nem mindig egyfolytában járjuk be. Meg lehet mutatni, hogy ekkor viszont a 0 pontba mindig ugyanolyan osztályú átlón érkezünk, amilyenen onnan utoljára elindultunk.
0;7,14,6,13,5,12,4,11,3,10,2,9,1,8,0;6,12,3,9,0;5,10,0;4,8,12,1,5,9,13,2,6,10,14,3,7,11,0;3,6,9,12,0;2,4,6,8,10,12,14,1,3,5,7,9,11,13,0;1,7,13,4,10,1;6,11,1;4,7,10,13,1;2;8,14,5,11,2;7,12,2;5,8,11,14,2;3;8,13,3;4;9,14,4;5;6;7;8;9;10;11;12;13;14;0.
*Lásd pl. Ruzsa I.‐Cser A.‐Könyves Tóth K.‐dr. Hajnal A.‐Bakos T.: Matematika, a matematikai osztályok számára, III. kötet, 325‐400 o., élesebben 363─355. o. Tankönyvkiadó, Budapest, 1966.

*Lásd pl. Kürschák J.‐Hajós Gy.‐Neukomm Gy.‐Surányi J.: Matematikai versenytételek, I. rész, 3. kiad., Tankönyvkiadó, Budapest, 1965, 46. o.