Feladat: 1475. matematika feladat Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Baróthy B. ,  Berács J. ,  Bottyán I. ,  Csörgei J. ,  Dobozy O. ,  Dombi J. ,  Egri R. ,  Farkas I. ,  Hunyadvári L. ,  Joó I. ,  Koren A. ,  Losonci Zoltán ,  Moson P. ,  Nádai L. ,  Orbán G. ,  Perémy G. ,  Szilléry A. ,  Szűcs A. ,  Tátray P. ,  Verdes S. ,  Vetier András 
Füzet: 1967/november, 111 - 115. oldal  PDF  |  MathML 
Témakör(ök): Geometriai egyenlőtlenségek, Vetítések, Kocka, Szabályos tetraéder, Tetraéderek, Feladat
Hivatkozás(ok):Feladatok: 1966/szeptember: 1475. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Könnyen elképzelhetjük a vizsgálandó alakzatot, ha a tetraéder 4 csúcsát egy K kocka 8 csúcsa közül jelöljük ki. Valóban az 1. ábra ABCD=T tetraéderének mind a 6 éle egyenlő, mert mindegyik a kocka egy lapjának átlója, tehát a tetraéder mindegyik lapja szabályos háromszög. Eszerint a T köré írt gömb azonos a K köré írt gömbbel. Legyen a középpontja 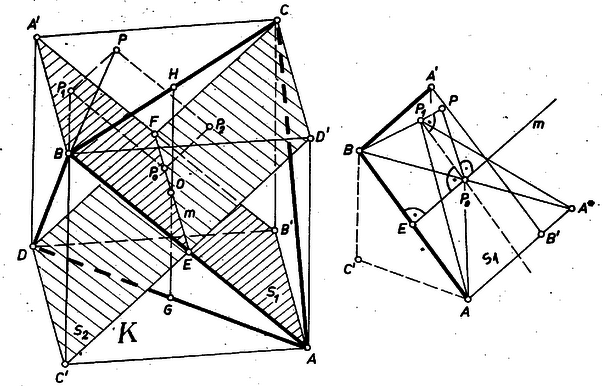O.

 
1. ábra

Legyen a tetszés szerinti P pont vetülete az AB él E és a CD él F felezőpontját összekötő m egyenesen P0. Megmutatjuk, hogy P-t a P0-ba áttolva a kérdéses távolságok összege csökken, hacsak nem P éppen azonos P0-lal.
Legyen P vetülete az ABF=S1 síkon P1, a CDE=S2 síkon P2, ekkor
PA+PB≥P1A+P1BésPC+PD≥P2C+P2D,(1)
mert pl. PA az APP1 derékszögű háromszögben átfogó, P1A pedig befogó. Egyenlőség akkor és csak akkor áll, ha ‐ a példát továbbvíve ‐ P rajta van S1-en, vagyis azonos P1-gyel. Összeadással (1)-ből
PA+PB+PC+PD≥P1A+P1B+P2C+P2D,(2)
ahol egyenlőség akkor és csak akkor áll, ha a P az S1 és S2 mindegyikén rajta van.
Nyilvánvaló, hogy a mondott m egyenes az S1, S2 síkok metszésvonala. A mondott P0 vetület pedig egyszersmind P1-nek és P2-nek is vetülete m-re. Ezt ‐ pl. P1-re ‐ csak akkor kell bizonyítanunk, ha P1 nem azonos sem P-vel, sem P0-lal. Ekkor m merőleges a PP1P0 síkra, hiszen m ‐ mivel benne van S1-ben ‐ merőleges PP1-re, másrészt szerkesztés folytán PP0-ra is, ennélfogva a P1P0 egyenes is merőleges m-re.
m merőleges AB-re is, CD-re is, mert E és F a kocka két párhuzamos lapjának középpontja, s így m párhuzamos az AB' éllel. Eszerint m az AB és CD élek közös felező merőlegese; ezért
(P1A+P1B)+(P2C+P2D)≥(P0A+P0B)+(P0C+P0D).(3)
Valóban, ha P1 nem azonos P0-lal, akkor véve A-nak A* tükörképét a P0P1 egyenesre, A* egyszersmind B tükörképe a P0 pontra, és így
P1A+P1B=P1A*+P1B≥A*B=P0A*+P0B=P0A+P0B.

(2) és (3) egybevetése állításunkat igazolja. Egyenlőség mindkét lépésben akkor és csak akkor áll, ha P1 is, P2 is azonos P0-lal, vagyis ha maga P azonos velük, vagyis P rajta van m-en.
Hasonló meggondolással, P0-t az AD, BC élpár közös GH felező merőlegesére vetítve olyan pontot kapunk, melyre nézve a T csúcsaitól mért távolságok összege ismét csökken, ill. változatlan marad. Ezzel azonban éppen O-ba jutunk, hiszen EF és GH itt metszik egymást és a kocka harmadik laptengelyét, ennélfogva további csökkentés nem lehetséges, a csúcsok O-tól mért távolságainak összege a lehetséges legkisebb érték.
 
 Losonci Zoltán (Szeged, Vedres I. Ép. Ip. T. IV. o. t.)
 

II. megoldás. Fektessünk az ABCD=T szabályos tetraéder minden egyes csúcsán át párhuzamos segédsíkot a szemben fekvő lappal, és legyen a tetszés szerinti P pontnak ezektől való távolsága rendre ta, tb, tc, td. Egy pont egy sík bármely pontjától legalább annyira van, mint a síktól való távolsága, ezért PA≥ta,...,PD≥td. Egyenlőség mindenütt akkor és csak akkor áll, ha P rajta van azon a merőlegesen, melyet az illető csúcsban állítunk a rajta felvett segédsíkra; azaz pl. PA=ta akkor és csak akkor áll, ha PA merőleges a BCD lap síkjára, vagyis P rajta van T-nek A-ból húzott magasságegyenesén. Továbbá
PA+PB+PC+PD≥ta+tb+tc+td,(4)
és egyenlőség csak akkor áll, ha P rajta van T-nek mind a négy magasság-egyenesén, vagyis azonos T-nek O középpontjával, hiszen szabályos tetraéder magasságai ‐ mint forgási szimmetriatengelyek ‐ átmennek O-n.
 
2. ábra

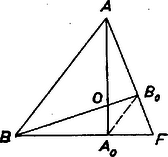A négy segédsík egy újabb A1B1C1D1=T1 szabályos tetraédert határoz meg, mert pl. az A-n át felvett segédsík 3-szorosára nagyított képe a BCD síknak, O-ból mint hasonlósági középpontból úgy, hogy a megfelelő pontpárok O két oldalán vannak. Valóban, O mindegyik magasságát 1:3 arányban osztja T-nek, mert pl. AA0, BB0 magasságának A0, B0 talppontja (2. ábra) középpontja a CDB, ill. CDA lapnak, tehát harmadolja a BF, ill. AF laptengelyt, ezért A0B0∥AB, és így OA0:OA=A0B0:AB=FA0:FB=1:3.
Legyen egyelőre P a T1-nek belső vagy felületi pontja, így alkalmazhatjuk a következő, alább bebizonyítandó segédtételt: szabályos tetraéder tetszés szerinti belső vagy felületi pontjára nézve a négy laptól mért távolságok összege állandó (egyenlő a tetraéder m1 magasságával). Mármost O-nak T1 lapjain levő vetülete a nagyítás miatt rendre az A, B, C, D csúcs, eszerint (4) jobb oldala egyenlő OA+OB+OC+OD-vel, tehát (4) éppen a feladat állítását fejezi ki.
Segédtételünk a T1-en kívüli P pontokra is érvényes, ha negatívnak vesszük mindazoktól a lapsíkoktól mért távolságokat, amelyek a pontot elválasztják T1 negyedik csúcsától. Állításunkban viszont a távolságok abszolút értéke szerepel. Ezt írva a negatívnak vett távolságok helyére, az összeg nagyobb lesz m1-nél ‐ hiszen a T1-re nézve külső pontok 1, 2 vagy 3 lapsíknak is a negyedik csúcstól elválasztott félterében vannak ‐, tehát PA+PB+PC+PD mindig nagyobb m1-nél.
A segédtétel bizonyítása céljára legyen a tetraédernek a P-n átmenő, a BCD lappal párhuzamos metszete B1C1D1, az AB1C1D1 tetraéder ACD-vel párhuzamos metszete P-n át A2C2D2, és az A2B1C2D2 tetraéd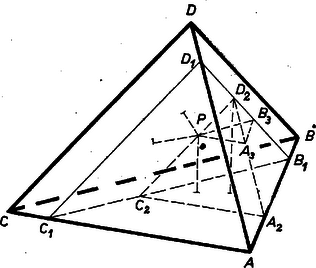er A2B1C2-vel párhuzamos metszete P-n át A3B3P (3. ábra).
 
3. ábra

Ekkor D2 távolsága az ABC laptól az A3B3PD2 tetraéder magasságával több, mint az A3B3P sík pontjainak, pl. P-nek a távolsága ettől a síktól; az említett magasság viszont a P-ből húzott magassággal, vagyis P-nek az ABD síktól való távolságával egyenlő. Viszont D2 távolsága az ACD és BCD síktól ugyanakkora, mint az A2C2D2, ill. a B1C1D1 sík bármely pontjáé, tehát mint pl. P-é. Így D2-nek a tetraéder lapjaitól mért távolságai összege ugyanannyi, mint P távolságösszege (az ABD síktól való távolsága 0).
Hasonlóan látható, hogy a távolságösszeg nem változik D2-ből B1-be, majd B1-ből A-ba menve át. A-nak viszont 3 laptól mért távolsága 0; a negyediktől mért távolsága pedig a tetraéder magassága. Ezzel segédtételünket bebizonyítottuk. Az olvasóra bízzuk annak átgondolását, hogy a bizonyítás, előjeles távolságokkal számolva, a tetraéderen kívül levő pontra is érvényes.
Vetier András (Budapest, Fazekas M. gyak. g. III. o. t.)
dolgozatából, kiegészítve a segédtétel számításmentes bizonyításával.

 
Megjegyzések. 1. Ha P a tetraéderen kívüli pont, akkor az alábbiak szerint mindig megadható olyan T-beli pont, melyre nézve a távolságösszeg kisebb, mint P-re nézve. Legyen T-nek P-hez legközelebbi pontja Q (megkaphatjuk pl. úgy, hogy egy P körüli gömb sugarát addig növeljük ‐ addig fújjuk fel ‐, amíg T-be ütközik, a beleütközési pont Q), továbbá T-nek egy tetszés szerinti, belső vagy a határon levő, Q-tól különböző pontja R. Ekkor P a QR szakasz felező merőleges síkjának azon az oldalán van, mint Q, és P-nek a QR egyenesen levő P' vetülete nem eshet a QR szakaszra, hiszen akkor P' a T belső pontja volna ‐ mivel T konvex ‐ és közelebb lenne P-hez, mint Q. Emiatt P' az RQ szakasz Q-n túli meghosszabbításán van, tehát
PR≥P'R>QR.
Eszerint Q a T minden pontjához határozottan közelebb van, mint P:
PA+PB+PC+PD>QA+QB+QC+QD.

Így nincs szükség arra, hogy a segédtételt külső pontokra is bizonyítsuk.
2. A segédtételt többen is térfogatszámítási ‐ azaz kissé távolabb álló ‐ meggondolással bizonyították be.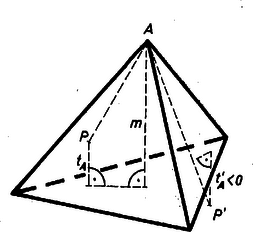
 
 
4. ábra
 

III. megoldás. Felhasználjuk az előző megoldás segédtételét, mely szerint a P pontnak a BCD, ACD, ABD, ABC lapoktól mért (előjeles) tA, tB, tC, tD távolságainak összege független a P pont helyzetétől (4. ábra).
Adjuk ezeket a távolságokat a csúcsoktól mért távolságok összegéhez, akkor a módosított összeg ugyanakkor lesz a legkisebb, mint az eredeti: De AP+tA nagyobb, mint a tetraéder m magassága, kivéve, ha P a magasságvonalon van, amikor AP+tA=m. Hasonló érvényes a PB+tB, PC+tC, PD+tD összegekre. Így a teljes összeg minden más pontra nagyobb, mint a magasságok metszéspontjára, ami azonos O-val.