Kezdőlap


Feladat:	1474. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Egri Róbert , Gyarmati Erzsébet , Sugár László
Füzet:	1967/november, 109 - 111. oldal		PDF \| MathML
Témakör(ök):	Trigonometrikus egyenletek, Trigonometriai azonosságok, Derékszögű háromszögek geometriája, Egyenlő szárú háromszögek geometriája, Szinusztétel alkalmazása, Feladat
Hivatkozás(ok):	Feladatok: 1966/szeptember: 1474. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Sem $α$ , sem $β$ nem derékszög, különben a föltevésnek nem volna értelme; továbbá $tg γ / 2 > 0$ , hiszen $γ / 2$ hegyesszög. Így (1)-et szorozva $cos α cos β cos γ / 2$ -vel, és tagjait $a$ és $b$ szerint rendezve

\begin{matrix} a cos β (cos α cos γ / 2 - sin α sin γ / 2) + b cos α (cos β cos γ / 2 - sin β sin γ / 2) = 0. \end{matrix}

A zárójelekre az addíció-tételt alkalmazva látjuk, hogy egyik a másiknak

- 1

-szerese, hiszen bennük

α + γ / 2

és

β + γ / 2

koszinusza áll, és e két szög egymás kiegészítő szöge. A föltevés így alakul:

\begin{matrix} cos (α + \frac{γ}{2}) (a cos β - b cos α) = 0, \end{matrix}

ami szerint legalább az egyik teljesül a

\begin{matrix} cos (α + \frac{γ}{2}) = 0, & (2) \\ a cos β = b cos α & (3) \end{matrix}

egyenlőségek közül.
Mármost (2)-ből

α + γ / 2

derékszög, így

β + γ / 2

is az, tehát (2) csak

α = β

esetén teljesül. (3) két oldala pedig a háromszög

C

-ből húzott magassága

C_{1}

talppontjának

B

-től, ill.

A

-tól vett távolsága, s mivel a

B C_{1} = A C_{1}

egyenlőség az

A B

egyenes pontjai közül csak az

A B

oldal felezőpontjára teljesül,

A C C_{1}

és

B C C_{1}

egybevágó derékszögű háromszögek,

A C = B C

. Ezek szerint az

A B C

háromszög mindenképpen egyenlő szárú.

Gyarmati Erzsébet (Budapest, Radnóti M. gyak. g. III. o. t.)

Megjegyzés. (3)-ból a színusz-tétel alkalmazásával is haladhatunk tovább:

\begin{matrix} \frac{cos α}{cos β} = \frac{a}{b} = \frac{sin α}{sin β}, sin (α - β) = 0, α = β . \end{matrix}

II. megoldás. (1) szimmetriája miatt választhatjuk a betűzést úgy, hogy

α \geq β

, azaz

a \geq b

legyen. Nem lehet

α

tompaszög, különben

\begin{matrix} 90^{\circ} > 180^{\circ} - α = β + γ > β \end{matrix}

miatt

\begin{matrix} | tg α | > tg β és | a tg α | > b tg β, \end{matrix}

és (1) jobb oldala negatív lenne, holott bal oldala pozitív. Derékszög sem lehet

α

, mert akkor a jobb oldalnak nem lenne értelme.
Megmutatjuk, hogy a

90^{\circ} > α > β

föltevést (1)-hez csatolva ellentmondásra jutunk. Ekkor

a > b

tg α > tg β

, így

(a - b) (tg α - tg β) > 0

-ból kifejtéssel:

\begin{matrix} a tg α + b tg β > a tg β + b tg α . \end{matrix}

Adjuk hozzá mindkét oldalhoz a bal oldalt ‐ így a jobb oldal szorzattá alakítható ‐, és osszuk az egyenlőtlenséget

2 tg (α + β) / 2

-vel. Ekkor a

tg (α + β) / 2 = 1 / tg (γ / 2)

azonosságra tekintettel a bal oldalon (1) jobb oldala áll:

\begin{matrix} 2 (a tg α + b tg β) > (a + b) (tg α + tg β), \\ tg \frac{γ}{2} (a tg α + b tg β) = a + b > (a + b) \cdot \frac{tg α + tg β}{2 tg \frac{α + β}{2}}, \end{matrix}

tehát

\begin{matrix} tg \frac{α + β}{2} > \frac{tg α + tg β}{2} . \end{matrix}

(4)

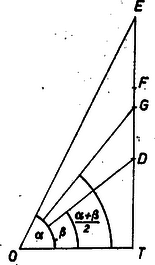1. ábra

Mérjük föl egy

T

csúcsú derékszög egyik szárára a

T O = 1

szakaszt, majd az

O T

egyenes ugyanazon oldalára

T O D ∢ = β

T O E ∢ = α

és

T O G ∢ = (α + β) / 2

szöget, ahol

D

E

G

rendre az új szár metszéspontja a derékszög másik szárával. Mivel

(α + β) / 2

ugyancsak hegyesszög, (4) szerint

\begin{matrix} T G > \frac{T E + T D}{2} = T F, D G > D F, \end{matrix}

ahol

F

D E

szakasz felezőpontja. Ez azonban lehetetlen, mert

O D < O E

, így az

O D E

háromszögben

O D E ∢ > 90^{\circ}

miatt

O E > O D

O G

felezi a

D O E

szöget, és így

\begin{matrix} \frac{D G}{G E} = \frac{O D}{O E} < 1, D G < G E, D G < \frac{D E}{2} = D F . \end{matrix}

Ezt akartuk bizonyítani. Eszerint (1) csak

α = β

esetén teljesülhet. Ekkor viszont teljesül is, hiszen így

γ / 2

pótszöge

α

-nak és

β

-nak,

tg γ / 2

reciproka

tg α = tg β

-nak.

Sugár László (Budapest, I. István g. IV. o. t.)

Megjegyzés. Trigonometriai azonosságok alapján bizonyítjuk, hogy (4) lehetetlen. A jobb oldal így alakítható:

\begin{matrix} \frac{sin (α + β)}{2 cos α cos β} & = \frac{sin \frac{α + β}{2} cos \frac{α + β}{2}}{cos α cos β} = \frac{tg \frac{α + β}{2} cos^{2} \frac{α + β}{2}}{cos α cos β} = \\ = \frac{tg \frac{α + β}{2} [1 + cos (α + β)]}{cos (α + β) + cos (α - β)}, \end{matrix}

így a bal és jobb oldal különbsége, kiemeléssel

\begin{matrix} tg \frac{α + β}{2} (1 - \frac{1 + cos (α + β)}{cos (α + β) + cos (α - β)}) = tg \frac{α + β}{2} \cdot \frac{cos (α - β) - 1}{2 cos α cos β} > 0. \end{matrix}

Eszerint, mivel a nevező tényezői pozitívok,

cos (α - β) > 1

, ami lehetetlen.

Egri Róbert (Budapest, Fazekas M. gyak. g. III. o. t.)

III. megoldás. Felhasználjuk a II. megoldásból, hogy

α

és

β

hegyesszögek. Azt mutatjuk meg, hogy

α > β

esetén az (1)-ből átrendezéssel adódó

\begin{matrix} a (tg α - cotg \frac{γ}{2}) = b (cotg \frac{γ}{2} - tg β) \end{matrix}

(5)

egyenlőség bal oldala nagyobb a jobb oldalánál.

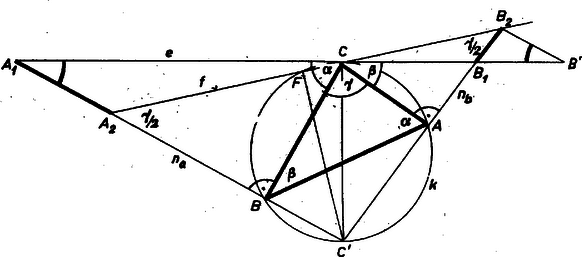2. ábra

Rajzoljuk meg az

A B C

háromszög

C

csúcsában a külső szög

f

felezőjét, és

k

körülírt kör

e

érintőjét, valamint a

C

-vel

k

-ban átellenes

C'

pontot

A

-val és

B

-vel összekötő

n_{b}

, ill.

n_{a}

egyenest.

e

és

f

különbözők, mert

f

metszi

k

-t, a

C

-t tartalmazó

A B

ív

F

felezőpontjában, ami

C

-től különböző (különben ugyanis

α = β

lenne);

F

A

-t nem tartalmazó

B C

ív pontja.

C'

C

-t nem tartalmazó

A B

ív belső pontja, különben nem állhatna

α

β < 90^{\circ}

n_{a}

merőleges

C B

-re,

n_{b}

pedig

C A

-ra. Legyen

n_{a}

és

n_{b}

metszéspontja

e

-vel

A_{1}

, ill.

B_{1}

f

-fel

A_{2}

, ill.

B_{2}

. Fennáll

\begin{matrix} A_{1} C B ∢ = α, B_{1} C A ∢ = β, C' A_{2} B_{2} ∢ = C' B_{2} A_{2} ∢ = γ / 2, \end{matrix}

utóbbiak azért, mert

C' A_{2} B_{2}

egyenlő szárú háromszög, ugyanis

C'

-nél levő szögét felezi a

C' F

egyenes, és

A_{2} B_{2}

oldala merőleges erre, továbbá a

C'

-nél levő szöge

180^{\circ} - γ

.
A keletkezett derékszögű háromszögek felhasználásával

\begin{matrix} A_{1} A_{2} = A_{1} B - A_{2} B = a (tg α - cotg \frac{γ}{2}) \\ B_{1} B_{2} = B_{2} A - B_{1} A = b (cotg \frac{γ}{2} - tg β), \end{matrix}

azaz (5) bal, ill. jobb oldala. Messe a

B_{2}

-n átmenő,

n_{a}

-val párhuzamos egyenes

f

-et

B'

-ben. Ekkor

A_{1} A_{2} > B' B_{2}

, ugyanis

C A_{1} A_{2}

és

C B' B_{2}

hasonló háromszögek, és bennük

C A_{2} > C B_{2}

, mert ‐ mint láttuk ‐

F

felezi

A_{2} B_{2}

-t, és

C

F B_{2}

szakasz belső pontja. Másrészt

B_{1} B_{2} < B' B_{2}

, mert a

B_{1} B_{2} B'

háromszög velük szemben fekvő szögeire

\begin{matrix} B_{1} B' B_{2} ∢ = C A_{1} B ∢ = 90^{\circ} - α < 90^{\circ} - β = B' B_{1} B_{2} ∢ . \end{matrix}

Így valóban

A_{1} A_{2} > B_{1} B_{2}

, amit bizonyítani akartunk.
Azt viszont hogy

α = β < 90^{\circ}

esetén teljesül (1), a II. megoldásban beláttuk.