Kezdőlap


Feladat:	1472. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bajmóczy Ervin , Balogh J. , Deák J. , Domokos László , Füvesi I. , Gegesy F. , Havas János , Herényi I. , Joó I. , Juhász Ágnes , Kádas S. , Kalmár I. , Lempert László , Nagy Elemér , Papp E. , Perémy G. , Pintér J. , Pintz J. , Szeredi P. , Szilágyi P. , Takács L. , Tiszai I.
Füzet:	1967/január, 19 - 21. oldal		PDF \| MathML
Témakör(ök):	Pont körüli forgatás, Síkra vonatkozó tükrözés, Gömbi geometria, Szabályos testek, Síkgeometriai számítások trigonometria nélkül, Feladat
Hivatkozás(ok):	Feladatok: 1966/május: 1472. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A II. elrendezés esetén a gömb sugara legalább 1 egységnyi. Ugyanis a középső síkon levő 6 ponttal meghatározott szabályos hatszög köré írt kör a gömbnek e síkkal való metszete, és e kör sugara legalább 1 egység, márpedig a gömb sugara nem lehet kisebb egy körmetszete sugaránál.
Megmutatjuk, hogy az I. elrendezés esetén a gömb sugara kisebb 1-nél; előbb azonban azt látjuk be, hogy az elrendezés megvalósítható. Ismeretes^{$^{*}$}, hogy egy $k_{0}$ körbe írható szabályos ötszög oldalának hosszát megadja a következő szerkesztés. Vesszük $k_{0}$ -nak két egymásra merőleges sugarát, $K B$ -t és $K L$ -et, és az utóbbinak $O$ felezőpontja körül írt $O B$ sugarú $k$ körrel metsszük a $K L$ egyenest az $A$ pontban $(A K < A L)$ , ekkor a keresett hosszúság $A B$ . (Az idézett helyen azt is láttuk, hogy $k$ és $K L$ másik metszéspontját $D$ -vel jelölve $B D$ megadja a $k_{0}$ -ba írt szabályos ötszög átlóját.)

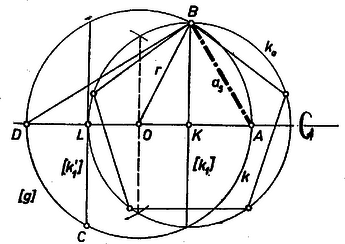1. ábra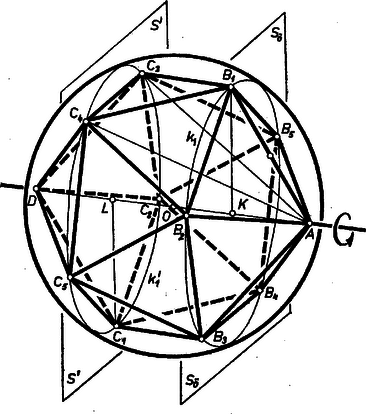

2. ábra

Ábránkat

A O

mint tengely körül forgatva

k

egy

O

középpontú

g

gömbfelületet ír le;

B

pedig egy

K

középpontú

k_{1}

kört, ennek sugara

K B

, eszerint a

k_{1}

-be írt szabályos ötszög oldala ugyancsak

A B

. Legyen egy ilyen ötszög

B_{1} B_{2} B_{3} B_{4} B_{5} = Ö

(legyen pl.

B_{1} = B

). Ekkor

Ö

csúcsai és

A

olyan helyzetben vannak egymáshoz képest, amilyet a feladat az első 5 pontra és a 11-ik pontra előír, az adódó szabályos ötoldalú gúlának mind a 10 éle egyenlő, tehát oldallapjai szabályos háromszögek, továbbá mindegyik csúcsa rajta van

g

-n. A gúlát az

A O

tengely körül

B_{1} K B_{2} ∢ = 72^{\circ}

-kal akárhányszor elfordítva önmagába megy át, ezért bármelyik két szomszédos oldallapjának szöge ugyanakkora.
A második 5 pont alakzatát

Ö

csúcsaihoz képest a kívánt helyzetben kapjuk a következők szerint. Tükrözzük az

A Ö

gúlát az

A B_{1}

él

S

felező merőleges síkjára. Ekkor a

B_{2}

és a

B_{5}

csúcs helyben marad,

A

és

B_{1}

helyet cserél;

B_{3}

és

B_{4}

képét jelöljük

C_{4}

-gyel, ill.

C_{3}

-mal (2. ábra). Ezek is

g

-n vannak, mert

A B_{1}

g

-nek húrja, és ezért

S

átmegy

O

-n. Forgassuk most el a gömböt

A O

körül

72^{\circ}

-kal úgy, hogy

B_{1}

B_{2}

-be menjen át. Ekkor

B_{5}

B_{1}

-be megy át, és így

C_{3}

C_{4}

-be, mert az

A B_{1} B_{5} C_{3}

tetraéder a vele egybevágó

A B_{2} B_{1} C_{4}

tetraéderbe megy át, hiszen az előbbi a

B_{1} A B_{5} B_{4}

képe, az utóbbi pedig a

B_{1} B_{2} A B_{3}

tetraéderé, ezek pedig egybevágók.
Legyen

C_{4}

elforgatott képe az előbbi forgatásban

C_{5}, C_{5}

-é

C_{1}

és

C_{1}

-é

C_{2}

. Ekkor

C_{2}

72^{\circ}

-kal elforgatott képe ismét

C_{3}

, hiszen ez a pont származtatható

C_{3}

5-szöri elforgatásával is.
A

C_{i}

csúcsok

(i = 1, 2, ..., 5)

A O

-ra merőleges, tehát

Ö

síkjával párhuzamos

S'

síkban vannak, és egy

Ö

-vel egybevágó

Ö'

szabályos ötszög csúcsai, hiszen a tükrözés miatt

C_{3} C_{4} = B_{4} B_{3}

. Ezért

Ö'

körülírt köre,

k'_{1}

, ami

g

és

S'

metszésvonala, egybevágó

k_{1}

-gyel, sugaraik egyenlők, így

S'

ugyanolyan messze van

O

-tól; mint

k_{1}

síkja, mert a gömb sugara és egy síkmetszet-körének sugara meghatározzák a metsző síknak a gömb középpontjától való távolságát. Eszerint

k'_{1}

k_{1}

-nek

O

-ra való tükörképe,

k'_{1}

középpontja

L

.
Továbbmenve mindegyik

C_{i}

pont a

B_{i}

-nek

O

-ra való tükörképe, mert pl. a

B_{1} B_{2}

gömbi húr felező merőleges síkja merőlegesen áll

k_{1}

és

k'_{1}

síkjára, belőlük

O

-ra tükrös pontpárokat metsz ki, és ezek egyike

B_{4}

és

C_{4}

. Ezért 12-ik pontként megfelel

D

, ami

A

-nak

O

-ra való tükörképe, hiszen így ez ugyanolyan helyzetben van

Ö'

csúcsaihoz képest, mint

A

Ö

csúcsaihoz képest. Mindezek szerint az

A

B_{i}

C_{i}

D

pontokból álló rendszer a

g

gömbön van, és minden pontnak a hozzá legközelebbi pontoktól való távolsága

A B

(hiszen

A C_{i} = B_{i} D = B_{1} B_{3} > B_{1} B_{2} = A B_{1}

)
Legyen mármost

g

sugara

O B = r

(1. ábra). Így az

O B K

derékszögű háromszögből

K O = K B / 2

figyelembevételével

K B = 2 r / \sqrt[]{5}

, ebből

\begin{matrix} K A = r (1 - \frac{1}{\sqrt[]{5}}), A B = \sqrt[]{K A^{2} + K B^{2}} = r \sqrt[]{\frac{10 - 2 \sqrt[]{5}}{5}}, \end{matrix}

és

A B = 1

lesz, ha az alakzatot úgy nagyítjuk, hogy

\begin{matrix} r = \sqrt[]{\frac{5}{10 - 2 \sqrt[]{5}}} = \sqrt[]{\frac{5 + \sqrt[]{5}}{8}} \end{matrix}

legyen. Ez pedig kisebb 1-nél, mert

\sqrt[]{5} < 3

. Ezt akartuk bizonyítani.

Lempert László (Budapest, Radnóti M. Gyak. Ált. Isk. és G., 8. o. t.)

Bajmóczy Ervin (Budapest, Ady E. Ált. Isk. és G., 7. o. t.)

Megjegyzések. 1. Rövidebben jutunk célba, ha eleve elfogadjuk, hogy az I. elrendezés lehetséges úgy, hogy a két szabályos gúla oldallapjai is szabályos háromszögek, a 12 pont egy szabályos ikozaéder csúcsainak rendszere, és köréje

g

gömb írható. Így ugyanis bármelyik ponthoz legközelebb álló 5 pont egy síkban van, és egy szabályos ötszög csúcsait adja, pl.

B_{1} A = B_{1} B_{2} = B_{1} C_{4} = B_{1} C_{3} = B_{1} B_{5}

miatt

A, B_{2}, C_{4}, C_{3}

és

B_{5}

egy a

B_{1}

körül

B_{1} A

sugárral írt

g_{1}

gömbfelület pontjai, rajta vannak

g

és

g_{1}

metszésvonalán, ami kör, vagyis síkidom.
Ekkor

B_{1} D = d

egy ilyen szabályos ötszög átlója,

B_{1} A = a

pedig oldala,

A D

a gömb és az

A B_{1} D

főkör átmérője, ezért az

A D B_{1}

derékszögű háromszögből.

4 r^{2} = a^{2} + d^{2}

. A II. elrendezésben viszont

4 r_{II}^{2} ≧ a^{2} + e^{2}

, ahol

e

a szabályos hatszög rövidebb átlójának hossza. Fennáll

e > d

, mert a szabályos hatszög egy szöge nagyobb a szabályos ötszögénél, ezért

r_{II} > r

Havas János (Budapest, Berzsenyi D. g. III. o. t.)

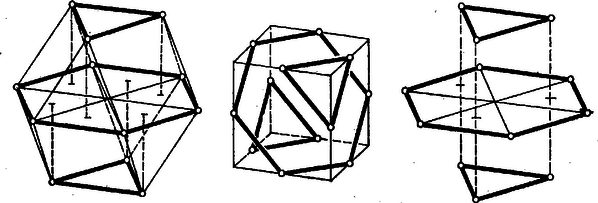3. ábra

2. A II. elrendezés megvalósítható egységnyi sugarú gömbön. Ugyanis az egységnyi oldalú szabályos hatszöget 6 szabályos háromszögre bontva és minden második háromszögre egységnyi élű szabályos tetraédert állítva, ezek új csúcsai a hatszög síkjával párhuzamos síkban fekvő egységnyi oldalú szabályos háromszöget alkotnak. ‐ A második szabályos háromszöget alkotó ponthármas 2-féleképpen is képezhető: a most kapottat vagy a hatszög középpontjára tükrözzük, vagy a hatszög síkjára. Az első eset elrendezése azonos egy kocka 12 él-felező pontjának rendszerével (3. ábra).

Domokos László (Tatabánya, Árpád g. IV. o. t.)

^{$^{*}$}Lásd pl. az 1213. feladatban, K. M. L. 27 (1963) 18-20. old.