Kezdőlap


Feladat:	1471. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Balogh József , Bod Judit , Bottyán I. , Csirmaz L. , Deák J. , Domokos L. , Fojt L. , Füvesi I. , Gegesy F. , Havas János , Herényi I. , Joó I. , Juhász Ágnes , Kádas S. , Kalmár I. , Kiss Á. , Kloknicer I. , Korchmáros G. , Külvári I. , Óhegyi E. , Palla L. , Papp E. , Papp Z. , Pintér J. , Rácz S. , Szeidl L. , Szentgáli Á. , Szeredi P. , Szilágyi P. , Tényi G. , Tolnay-Knefély T. , Varga Gabriella
Füzet:	1968/február, 50 - 53. oldal		PDF \| MathML
Témakör(ök):	Gyökök és együtthatók közötti összefüggések, Egyenesek egyenlete, Feladat
Hivatkozás(ok):	Feladatok: 1966/május: 1471. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. I. Minden az adott $a$ , $b$ , $c$ helyeken a $0$ értéket felvevő harmadfokú függvény a következő alakra hozható:

\begin{matrix} y = k (x - a) (x - b) (x - c) = k (x^{3} - (a + b + c) x^{2} + (a b + b c + c a) x - a b c), \end{matrix}

(1)

ahol

k

alkalmas,

0

-tól különböző állandó. Keressük egyszerűség kedvéért a függvényt ábrázoló görbe érintőjét egyelőre a tetszés szerinti

x_{1}

abszcisszájú

P_{1}

pontban, azután alkalmazzuk majd az eredményt a kérdéses

x_{1} = (a + b) / 2

esetre.

P_{1}

ordinátája

\begin{matrix} y_{1} = k (x_{1}^{3} - (a + b + c) x_{1}^{2} + (a b + b c + c a) x_{1} - a b c) . \end{matrix}

Legyen a görbe egy más,

P_{2}

pontjának abszcisszája

x_{2}

, ekkor ordinátája

\begin{matrix} y_{2} = k (x_{2}^{3} - (a + b + c) x_{2}^{2} + (a b + b c + c a) x_{2} - a b c), \end{matrix}

és a

P_{1} P_{2}

szelő iránytangense

m_{12} = (y_{2} - y_{1}) / (x_{2} - x_{1})

. Forgassuk a szelőt

P_{1}

körül úgy, hogy

x_{2}

mind kevésbé térjen el

x_{1}

-től, ekkor a

P_{2}

pont közeledik a görbén

P_{1}

- hez és a szelő határhelyzete az érintő lesz, arra az esetre, ha

P_{2}

egybeesik

P_{1}

-gyel.

m_{12}

számlálójának

k

-adrésze alkalmas kiemelésekkel így alakítható:

\begin{matrix} \frac{y_{2} - y_{1}}{k} = (x_{2}^{3} - x_{1}^{3}) - (a + b + c) (x_{2}^{2} - x_{1}^{2}) + (a b + b c + c a) (x_{2} - x_{1}) = \\ = (x_{2} - x_{1}) (x_{2}^{2} + x_{1} x_{2} + x_{1}^{2} - (a + b + c) (x_{2} + x_{1}) + a b + b c + c a) . \end{matrix}

Ennélfogva mindenesetre

\begin{matrix} m_{12} = k (x_{2}^{2} + x_{1} x_{2} + x_{1}^{2} - (a + b + c) (x_{2} + x_{1}) + a b + b c + c a), \end{matrix}

a mondott határhelyzetben, mivel

x_{2} = x_{1}

\begin{matrix} m_{1} = k (3 x_{1}^{2} - 2 (a + b + c) x_{1} + a b + b c + c a), \end{matrix}

és ekkor az érintő egyenlete

\begin{matrix} y - y_{1} = m_{1} (x - x_{1}) . \end{matrix}

(2)

Könnyű belátni, hogy

m_{1}

zárójeles kifejezése három szorzat összegévé alakítható:

\begin{matrix} m_{1} = k ((x_{1} - a) (x_{1} - b) + (x_{1} - b) (x_{1} - c) + (x_{1} - c) (x_{1} - a)) . \end{matrix}

(3)

Ezzel beláttuk, hogy az

(y_{2} - y_{1}) / (x_{2} - x_{1})

kifejezés

x_{2} = x_{1}

esetén is meghatározza az (érintőbe átmenő) szelő meredekségét.
II. Írjuk most (3)-ban és (2)-ben

x_{1}

y_{1}

helyére az előírt, ill. (1)-ből adódó

\begin{matrix} x_{1} = \frac{a + b}{2}, y_{1} = k (\frac{a + b}{2} - a) (\frac{a + b}{2} - b) (\frac{a + b}{2} - c) \end{matrix}

értékeket, így megkapjuk a kérdéses érintő egyenletét, és azt kell belátnunk, hogy ezt az

x = c

y = 0

pont kielégíti, vagyis hogy fennáll

\begin{matrix} - y_{1} = m_{1} (c - x_{1}) . \end{matrix}

(4)

A jobb oldal első tényezője (3) alapján így alakítható:

\begin{matrix} m_{1} = k (x_{1} - a) (x_{1} - b) + k (x_{1} - c) (2 x_{1} - a - b) = k (\frac{a + b}{2} - a) (\frac{a + b}{2} - b), \end{matrix}

hiszen a második tag

0

; vagyis

m_{1}

egyenlő

y_{1}

szorzat alakja első három tényezőjének szorzatával. (4) második tényezője pedig a behelyettesítéssel egyenlővé válik

y_{1}

utolsó tényezőjének

(- 1)

-szeresével, tehát (4) valóban teljesül. Ezzel az állítást bebizonyítottuk.
Balogh József (Hatvan, Bajza J. G.)
Varga Gabriella (Szombathely, Savaria G.)

Megjegyzés. Az

a

b

c

abszcisszák nagyságviszonyáról semmit sem tételeztünk fel, ennélfogva pl. az;

\begin{matrix} y = 0, 2 (x + 2) (x - 1) (x - 5) \end{matrix}

függvény esetében

c

szerepét a

- 2

+ 1

+ 5

zérushelyek mindegyike felveheti, vagyis e függvény grafikonjához három az állításnak megfelelő érintő húzható.

y = 0,2 (x + 2) (x - 1) (x - 5)

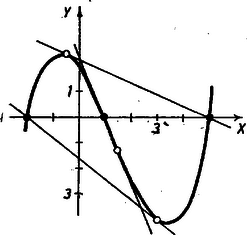
Azt sem használtuk fel, hogy

a

b

c

különbözők, sem azt, hogy

(a + b) / 2

és

c

különbözők. Pl. az

\begin{matrix} y = (x + 3) (x - 2) (x - 7) / 12 \end{matrix}

függvény esetében a középső zérushely éppen egyenlő a legkisebb és legnagyobb zérushely számtani közepével.

y = (x + 3) (x - 2) (x - 7) / 12

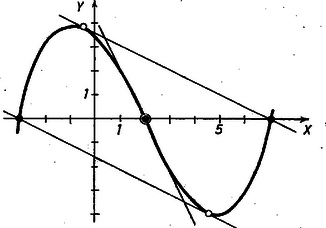
II. megoldás. Az állítás következő megfordítását bizonyítjuk: az

y = k (x - a) (x - b) (x - c)

függvény

g

grafikonjának

C (c,0)

pontjából a görbéhez húzott érintő érintési pontjának abszcisszája

(a + b) / 2

. A

C

ponton átmenő tetszés szerinti

e

egyenes egyenlete

y = m (x - c)

, ahol

m

tetszés szerinti állandó.

g

és

e

további két metszéspontjának abszcisszája a

\begin{matrix} k (x - a) (x - b) (x - c) = m (x - c) \end{matrix}

egyenletből adódik. Az érdektelen

C

metszéspontra vezető

x - c

tényezőt mindkét oldalon elhagyva:

\begin{matrix} k (x - a) (x - b) = m, azaz k x^{2} - k (a + b) x + k a b - m = 0. \end{matrix}

A két metszéspont

x_{1}

és

x_{2}

abszcisszájának számtani közepe a gyökök és együtthatók közti összefüggés alapján mindenesetre

\begin{matrix} \frac{1}{2} (x_{1} + x_{2}) = \frac{1}{2} \frac{k (a + b)}{k} = \frac{a + b}{2}, \end{matrix}

ez tehát akkor is áll, ha

e

-nek azt a helyzetét vesszük, amelyben

x_{1} = x_{2}

, vagyis amikor

e

éppen érintő. Ekkor

(x_{1} + x_{2}) / 2 = x_{1} = (a + b) / 2

, ezt akartuk bizonyítani.
Ebből azért következik a feladat állítása, mert a harmadfokú függvény grafikonjának minden egyes pontjában egyetlen érintője van. Láttuk ugyanis az I. megoldás (3) kifejezésében, hogy

P_{1}

-nek

x_{1}

abszcisszája egyértelműen meghatározta az érintő iránytangensét.
Juhász Ágnes (Budapest, Berzsenyi D. G.)

Megjegyzés. Itt az érintő definiciójából csak ennyit használtunk ki: olyan egyenes, melynek a görbével való metszéspontjai közül kettő egybeesik.

III. megoldás (vázlat). Messe az

y = p x + q

egyenes az

y = k (x - a) (x - b) (x - c)

függvény grafikonját az

x_{1}

x_{2}

x_{3}

abszcisszájú pontokban. Az abszcisszák a

\begin{matrix} k (x - a) (x - b) (x - c) - (p x + q) = 0 \end{matrix}

(5)

egyenlet gyökei, így összegük a harmadfokú egyenlet gyökei és együtthatói közti összefüggés alapján egyenlő az

x^{2}

és

x^{3}

előtt álló együtthatók hányadosának

(- 1)

-szeresével. Ez (5) polinommá alakítása alapján

\begin{matrix} x_{1} + x_{2} + x_{3} = a + b + c . \end{matrix}

Ha most azt az egyenest vesszük, amelyre

x_{1} = x_{2} = (a + b) / 2

, akkor

x_{3} = c

. És fordítva, ha

x_{3} = c

, és

x_{1} = x_{2}

, akkor

x_{1} = (a + b) / 2

.
Havas János (Budapest, Berzsenyi D. G.)