Kezdőlap


Feladat:	1470. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bajmóczy E. , Czeizler András , Deák J. , Domokos László , Fövényesi Ildikó , Gajdács Ibolya , Gegesy Ferenc , Havas J. , Herényi I. , Joó I. , Kádas S. , Kafka Péter , Kiss A. , Kloknicer I. , Langer Tamás , Losonci Z. , Nagy Elemér , Recski A. , Szeredi P. , Szilágyi P. , Tényi G. , Tolnay-Knefély T.
Füzet:	1967/október, 53 - 54. oldal		PDF \| MathML
Témakör(ök):	Négyszögek geometriája, Háromszögek geometriája, Szabályos sokszögek geometriája, Feladat, Síkidomok átdarabolása
Hivatkozás(ok):	Feladatok: 1966/május: 1470. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Elegendő egy olyan feldarabolást megadni, amelynél a darabokból két egybevágó szabályos nyolcszöget lehet összerakni. Ekkor ugyanis a kisebb nyolcszögekre újra alkalmazva az ilyen feldarabolást, a $k$ -adik lépés után $2^{k}$ darab egybevágó szabályos nyolcszöggé tudunk átalakítani egy szabályos nyolcszöget, tehát $k = 2$ , ill. $k = 3$ mellett 4, ill. 8 nyolcszöggé.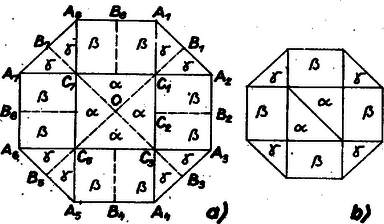

1. ábra

Az 1a ábra

c

oldalú szabályos nyolcszögét az

A_{1} A_{4}

A_{3} A_{6}

A_{5} A_{8}

A_{7} A_{2}

átlók nyilvánvalóan a

c

oldalú

C_{1} C_{3} C_{5} C_{7}

négyzetre, négy db egybevágó,

c

átfogójú és

c / \sqrt[]{2}

befogójú egyenlő szárú derékszögű háromszögre (pl.

A_{1} A_{2} C_{1}

) és négy db egybevágó téglalapra osztják, melyeknek oldalai

c

és

c / \sqrt[]{2}

(pl.

A_{2} C_{1} C_{3} A_{3}

). Továbbmenve, e részeket a

B_{1} B_{5}

és

B_{3} B_{7}

szimmetriatengelyek, ill. a

B_{2} B_{6}

B_{4} B_{8}

tengelyek berajzolt részei együttesen 4, 8, ill. 8 egybevágó

α

β

ill.

γ

jelű háromszögre, ill. téglalapra osztják, ahol a befogók hossza

α

-ban

c / \sqrt[]{2}

γ

-ban

c / 2

, az átfogóé rendre

c

, ill.

c / \sqrt[]{2}

, az oldalak

β

-ban

c / \sqrt[]{2}

és

c / 2

. A részekből az 1b ábra szerint (2

α

és 4‐4

β

, ill.

γ

jelű részből) összeállított 2 db szabályos nyolcszög megfelel tervünknek. Ezt bizonyítja az összes részek felhasználása, másrészt az, hogy az összeállított és az eredeti nyolcszög oldalainak aránya

1 : \sqrt[]{2}

, így területeik aránya

1 : 2

. Ezt akartuk bizonyítani, és ezzel a feladatot az előrebocsátottak szerint megoldottuk.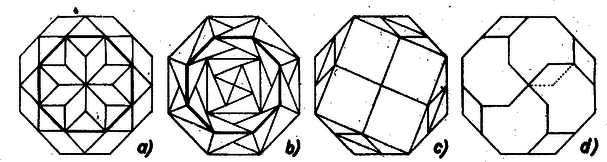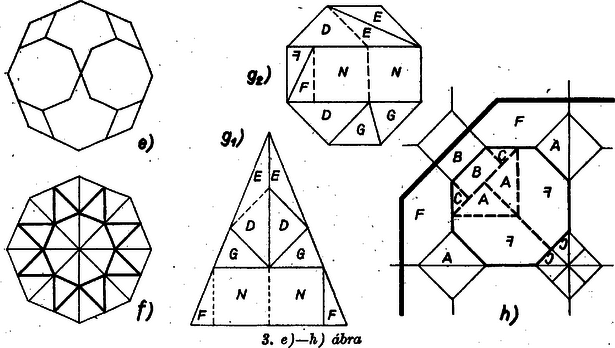

Czeizler András (Budapest, Ybl M. Ép. ip. t. III. o. t.)

3. ábra

Megjegyzés. A dolgozatok sokféle megoldást tartalmaznak, csak az 1. és a 3f ábra megoldása ismétlődik többször. Vázolunk néhány további érdekesebb átdarabolást. A 2. ábrán

N

n

v

négyzetek,

T

t

τ

egymáshoz hasonló téglalapok,

R

r

ϱ

rombuszok,

D

d

δ

derékszögű egyenlő szárú háromszögek, és

N = 4 n = 8 v

T = 4 t = 8 τ

R = 4 r = 8 ϱ

D = 4 d = 8 δ

. Továbbá

T = 2 R

, mert

T

alapja is, magassága is

\sqrt[]{2}

-ször akkora, mint

R

megfelelő mérete (hasonlóan

N = 2 D

is felhasználható lenne), ezért

T = 16 ϱ

és

R = 4 τ

, és a feldarabolást a következő jelképes egyenlőségek adják meg: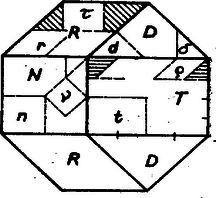

\begin{matrix} \frac{S_{8}}{4} & = \frac{N + 2 D + T + 2 R}{4} = n + 2 d + t + 2 r; \\ \frac{S_{8}}{8} & = v + 2 δ + τ + 2 ϱ . \end{matrix}

2. ábra

Mellékfeltételként arra is törekedhetünk, hogy a kisebb nyolcszögeket (vagy legalább néhányat közülük) minél kevesebb darabból állíthassuk össze.
A 3a‐3e ábra rendre Gegesy Ferenc (Budapest, Móricz Zs, g. I. o. t.), Langer Tamás (Budapest, Apáczai Csere J. gyak. g. III. o. t.), Fövényesi Ildikó (Miskolc, Ip. Szakközépiskola, III. o. t.), Kafka Péter (Pannonhalma, Bencés g. III. o. t.), Domokos László (Tatabánya, Árpád g. IV. o. t.) dolgozatából való. Érdekesek a rokonságok. Több esetben magában az ábrában ‐ vastag keretben ‐ mutatjuk meg a kisebb nyolcszög összeállítását, pl. a 3a ábra vastag kerületű nyolcszöge egészben marad, itt állítjuk össze a külső részekből a második nyolcszöget.