| Feladat: | 1462. matematika feladat | Korcsoport: 16-17 | Nehézségi fok: - |
| Megoldó(k): | Antos P. , Balázs Katalin , Baróthy B. , Bod Judit , Csirmaz L. , Cziffra A. , Dabóczi Á. , Deák J. , Dévényi K. , Domokos László , Farkas I. , Fencsik G. , Ferencz L. , Gács P. , Herényi I. , Horváth S. , Joó I. , Juhász Ágnes , Kloknices I. , Korchmáros G. , Langer T. , Medgyesy K. , Medveczky M. , Nédai L. , Papp Z. , Radó P. , Recski A. , Szabó Klára , Szeidl L. , Szeredi Péter , Tiszai István , Verdes S. | ||
| Füzet: | 1967/november, 107 - 108. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Háromszögek hasonlósága, Trigonometriai azonosságok, Derékszögű háromszögek geometriája, Egyenlő szárú háromszögek geometriája, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1966/április: 1462. matematika feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás. a) Az ábrát az alábbiak szerint kapjuk az középpontú, sugarú körből és az alkalmas külső pontból kiindulva. 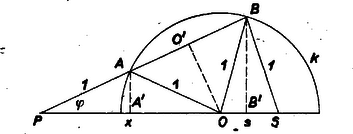 Legyen és a körüli, sugarú kör egyik metszéspontja , messe a egyenes -t másodszor -ben úgy, hogy , végül messe a körüli, sugarú kör a szakasz -n túli meghosszabbítását -ben. Így , és egyenlő szárú háromszögek. Legyen még , és vetülete -ra, ill. -ra rendre , , , továbbá ; ekkor , azaz
-re addig teljesül , míg tompaszög, azaz míg , továbbá -re addig teljesül , míg , egybevetve, míg . b) A szög értéke egyértelműen meghatározza az ábrát, s így és értékét is. Az adott értékek mellett ‐ amelyekre teljesül a feltétel ‐ valamelyik meghatározására nyerhetünk (1)-ből egyenletet. esetén , és , a háromszög egyenlő szárú, , (2) alapján
c) esetén , tehát , -re pedig (1)-ből az Szeredi Péter (Budapest, II. Rákóczi F. G.) II. megoldás a feladat első részéhez. és kifejezhetők -vel: , , így (1) helyett azt kell bizonyítanunk, hogy a csupán egy változót tartalmazó
azonosság más alakja. Az összefüggést a szögekre is kiterjeszthetjük. Ekkor célszerű az -vel egyirányú -t tekinteni pozitívnak, s így |