Kezdőlap


Feladat:	1460. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bottyán István , Csóka Géza , Karsai István , Külvári István
Füzet:	1967/május, 215 - 217. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Középpontos és egyéb hasonlósági transzformációk, Derékszögű háromszögek geometriája, Szélsőérték-feladatok differenciálszámítás nélkül, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1966/április: 1460. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük $E$ merőleges vetületét $A C$ -n $E_{1}$ -gyel, ekkor $E_{1} E = C F$ és $A E_{1} E ▵ \sim A C B ▵$ , így $C F$ ugyanakkor a legkisebb, amikor 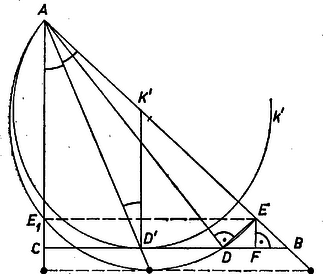$A E$ .

\begin{matrix} 1. ábra \end{matrix}

A E

mint átmérő fölé rajzolt félkör átmegy a

C B

oldal

D

pontján és megfordítva, ha egy félkör

A E

átmérője

A B

-n van és a félkör átmegy

B C

egy

D

pontján, akkor

D E ⊥ A D

, s így

E

és

C B

-n levő

F

vetülete a feladatban leírt módon keletkező pontok.
Így a feladatot visszavezettük a következőre: keressük a legkisebb átmérőjű félkört, amelyiknek

A E

átmérője az

A B

egyenesen van és amelyiknek van közös pontja

B C

-vel. Megmutatjuk, hogy ez a

B C

-t érintő félkör. Húzzuk meg ugyanis egy tetszés szerinti leírt tulajdonságú félkörnek a

B C

-vel párhuzamos érintőjét. Ez az

A B

és

A C

egyenesekkel egy

A B C

-hez hasonló és azt tartalmazó háromszöget zár be; így belőle kicsinyítéssel kapjuk az

A B C

háromszöget és benne a

B C

oldalt érintő félkört. Az utóbbi félkör átmérője tehát a legkisebb a vizsgált félkörök közt, amint állítottuk. Legyen ekkor

k'

középpontja

K'

, az érintési pont

D'

, így

B C ⊥ K' D' ∥ A C

, és

A D' K'

egyenlő szárú háromszög, ezért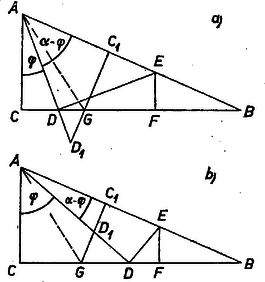

\begin{matrix} K' A D' ∢ = K' D' A ∢ = D' A C ∢, \end{matrix}

tehát a legrövidebb

C F

-re és legrövidebb

A E

szakaszra vezető

D

pontot a

C A B

szög felezője metszi ki a

C B

befogóból.

II. megoldás. A szerkesztés folytán

D E F

és

A D C

hasonló háromszögek,

\begin{matrix} D F = A C \cdot \frac{D E}{A D}, \end{matrix}

vagyis

D F

hosszát az

A D E

derékszögű háromszög kicsinyítésével is megkapjuk,

A

-ból induló befogóját

A C

hosszúságúnak véve, ekkor a keresett hossz a másik befogó. Egyszerűen kapjuk ezt,

A C

-t az

A B

egyenesre fölmérve, és a

C_{1}

végpontban állított merőlegessel metszve az

A D

egyenest

D_{1}

-ben; így

C_{1} D_{1} = D F

, és

C F = C D + C_{1} D_{1}

. Ekkor a

C_{1} D_{1}

egyenes a

C B

tükörképe a

C A B

szög felezőjére nézve, ezért a

C B

C_{1} D_{1}

egyenespár

G

metszéspontja rajta van a szögfelezőn.

\begin{matrix} 2. ábra \end{matrix}

D

-t éppen

G

-ben vettük fel, akkor

D_{1}

is itt adódik, és

C F = C D + D F = C G + C_{1} D_{1} = C G + C_{1} G = 2 \cdot C G

. Megmutatjuk, hogy

D

minden más helyzetében

C F > 2 C G

, vagyis

D

keresett helyzete éppen a

G

pont. A

C D < C G

esetre szorítkozunk (

2. a

ábra), a

C G < C D < C B

eset hasonló átgondolását az olvasóra hagyjuk (

2. b

ábra).

C D < C G

miatt

C A D ∢ < C A B ∢ / 2

D_{1}

C B

-nek

A

-t nem tartalmazó partján adódik. A

D D_{1} G

háromszögben

\begin{matrix} D_{1} D G ∢ = A D C ∢ = 90^{\circ} - C A D ∢ > 90^{\circ} - C_{1} A D_{1} ∢ = A D_{1} C_{1} ∢ = D D_{1} G ∢, \end{matrix}

ezért

D_{1} G > D G

, tehát

C F = C D + C_{1} G + G D_{1} > C D + C_{1} G + D G = C G + C_{1} G = 2 C G

, amit bizonyítani akartunk.

Csóka Géza (Ajka, Bródy I. g. III. o. t.)
Bottyán István (Hatvan, Bajza J. g. III. o. t.)

III. megoldás.

D E F

és

A D C

, valamint

E F B

és

A C B

hasonló derékszögű háromszögek (1. ábra), ezért

A C = b

C B = a

C D = x

C F = y

és

A B = c

jelöléssel egyrészt

\begin{matrix} D F = E F \cdot \frac{b}{x}, y = x + \frac{b}{x} \cdot E F, másrészt \\ \frac{E F}{b} = \frac{F B}{a} = \frac{a - y}{a}, E F = b - \frac{b}{a} \cdot y, tehát y = x + \frac{b^{2}}{x} - \frac{b^{2}}{a x} \cdot y, \\ y = a \cdot \frac{x^{2} + b^{2}}{a x + b^{2}} . & (1) \end{matrix}

A törtet eltávolítva, az egyenletet 0-ra redukálva és a bal oldalt teljes négyzetté kiegészítve:

\begin{matrix} 0 = a x^{2} - a x y + b^{2} (a - y) = a {(x - \frac{y}{2})}^{2} + b^{2} (a - y) - a \frac{y^{2}}{4}; \\ a {(x - \frac{y}{2})}^{2} = \frac{a}{4} \cdot y^{2} + b^{2} y - a b^{2} = a [{(\frac{y}{2} + \frac{b^{2}}{a})}^{2} - b^{2} \cdot \frac{a^{2} + b^{2}}{a^{2}}] = \\ = a [{(\frac{y}{2} + \frac{b^{2}}{a})}^{2} - \frac{b^{2} c^{2}}{a^{2}}] . \end{matrix}

Itt a betűk pozitív távolságokat jelentenek, tehát a bal oldal nem negatív, s így a jobb oldal sem lehet az.

y

értéke ugyanakkor a legkisebb, amikor a szögletes zárójelbeli első tagé, tehát amikor

\begin{matrix} \frac{y}{2} + \frac{b^{2}}{a} = \frac{b c}{a}, y = \frac{2 b (c - b)}{a} . \end{matrix}

Ekkor

\begin{matrix} x = \frac{y}{2} = \frac{b (c - b)}{a} = a \cdot \frac{b (c - b)}{a^{2}} = a \cdot \frac{b (c - b)}{c^{2} - b^{2}} = a \cdot \frac{b}{c + b}, \end{matrix}

amiben felismerjük a szögfelező lemetszette szakaszt.

Külvári István (Budapest, Széchenyi I. g. III. o. t.)

Megjegyzés. A fentieket megkaphatjuk trigonometriai úton is. Legyen

A C = 1

C A D ∢ = φ

C A B ∢ = α

, így

D A B ∢ = α - φ

, továbbá

C D = tg φ

A D = 1 / cos φ

D E = A D tg (α - φ)

D F = D E cos φ = tg (α - φ)

, és az addíció tétellel, a nevezőben adódó szorzatot összeggé alakítva

cos u cos v = [cos (u + v) + cos (u - v)] / 2

alapján, végül a nevezőt növelve

\begin{matrix} C F = \frac{sin φ}{cos φ} + \frac{sin (α - φ)}{cos (α - φ)} = \frac{sin (φ + α - φ)}{cos φ cos (α - φ)} = \frac{2 sin α}{cos (φ + α - φ) + cos (2 φ - α)} \geq \\ \geq \frac{2 sin α}{cos α + 1} = 2 \sqrt[]{\frac{1 - cos^{2} α}{{(1 + cos α)}^{2}}} = 2 \sqrt[]{\frac{1 - cos α}{1 + cos α}} = 2 tg \frac{α}{2}, \end{matrix}

továbbá egyenlőség csak

cos (2 φ - α) = 1

2 φ - α = 0

φ = α / 2

esetén áll fönn.
Hasonlóan, valamivel egyszerűbben

\begin{matrix} A E = \frac{A D}{cos (α - φ)} = \frac{1}{cos φ cos (α - φ)} \geq \frac{2}{cos α + 1} = \frac{1}{cos^{2} α / 2} . \end{matrix}

Karsai István (Szeged, Radnóti M. g. III. o. t.)