Kezdőlap


Feladat:	1456. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Domokos László , Kádas Sándor , Szeredi Péter
Füzet:	1967/március, 104 - 106. oldal		PDF \| MathML
Témakör(ök):	Fizikai jellegű feladatok, Terület, felszín, Szögfüggvények, síkgeometriai számítások, Körök, Feladat
Hivatkozás(ok):	Feladatok: 1966/március: 1456. matematika feladat

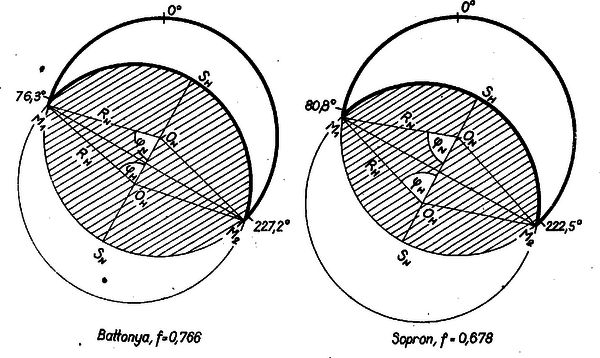
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A Napot és a Holdat ábrázoló körök közös részének területét kell kiszámítanunk a két sugár és középpontjaik távolsága ismeretében. Ugyanis a sugarak arányosnak vehetők az adott látószögekkel, mert 1) a fényképen a kör sugara arányos a látószög felének tangensével, 2) minden hegyesszög ívmértéke a szinusza és a tangense közé esik, 3) az adott szögek szinusza és tangense $4$ tizedesre kerekítve egyenlő, tehát ugyanez áll ívmértékükre is; másrészt a két kör középpontját $O_{N}$ , $O_{H}$ , a sugarakat $R_{N}$ , $R_{H}$ , az $O_{N} O_{H}$ szimmetriatengelynek a közös részbe eső szakaszát határoló metszéspontokat $S_{N}$ , $S_{H}$ és a legnagyobb fázis arányszámát $f$ betűvel jelölve

\begin{matrix} S_{N} S_{H} = f \cdot 2 R_{N} = S_{N} O_{N} - O_{H} O_{N} + O_{H} S_{H} = R_{N} + R_{H} - O_{N} O_{H}, \end{matrix}

tehát a középpontok távolsága az adatokból valóban kiszámítható:

\begin{matrix} O_{N} O_{H} = R_{H} - (2 f - 1) R_{N} . \end{matrix}

A közös részt a körök

M_{1} M_{2}

közös húrja két körszeletre vágja szét. A közös húrhoz tartozó középponti szög mindegyik körben

2

-szer akkora, mint az

O_{N} O_{H} M_{1}

háromszög megfelelő

φ_{N}

, ill.

φ_{H}

szöge. Ezekkel a közös rész területe, a szöget ívmértékben értve:

\begin{matrix} t = \frac{R_{N}^{2}}{2} (2 φ_{N} - sin 2 φ_{N}) + \frac{R_{H}^{2}}{2} (2 φ_{H} - sin 2 φ_{H}), \end{matrix}

és a szögeket a koszinusz-tétel alapján számíthatjuk ki:

\begin{matrix} cos φ_{N} = \frac{R_{N}^{2} + (O_{N} O_{H} - R_{H}) (O_{N} O_{H} + R_{H})}{2 R_{N} \cdot O_{N} O_{H}} = \\ = \frac{R_{N} - (2 f - 1) [2 R_{H} - (2 f - 1) R_{N}]}{2 \cdot O_{N} O_{H}} = \frac{[f^{2} + {(1 - f)}^{2}] R_{N} - (2 f - 1) R_{H}}{O_{N} O_{H}}, \end{matrix}

és hasonlóan

\begin{matrix} cos φ_{H} = \frac{1}{R_{H} \cdot O_{N} O_{H}} [R_{H}^{2} - (2 f - 1) R_{H} R_{N} - 2 f (1 - f) R_{N}^{2}] . \end{matrix}

A keresett arányszám:

\begin{matrix} k = \frac{t}{π R_{N}^{2}} = \frac{1}{2 π} [(2 φ_{N} - sin 2 φ_{N}) + {(\frac{R_{H}}{R_{N}})}^{2} \cdot 2 φ_{H} - sin 2 φ_{H})] . \end{matrix}

A látószög szögmásodpercben vett mértékszáma a Napra

1899

, a Holdra

1866

, mindjárt ezeket tekintjük

R_{N}

, ill.

R_{H}

alkalmas mértékegységben vett mértékszámának. Ekkor

O_{N} O_{H}

hossza Battonya esetében

855, 7

egység, Sopron esetében

1190

egység^{$^{*}$}, továbbá

{R_{H} / R_{N})}^{2} = 0, 9655

.
Battonya esetében

f = 0, 766

1 - f = 0, 234

2 f - 1 = 0, 532

, így a fenti szögek, valamint

x - sin x

értéke a

2

-szeres szögekre

\begin{matrix} cos φ_{N} = \frac{(0, 5868 + 0, 0548) 1899 - 0, 532 \cdot 1866}{855, 7} = \frac{1219 - 993}{855, 7}, \\ φ_{N} = {74, 69}^{\circ} = 1, 304, 2 φ_{N} - sin 2 φ_{N} = 2, 608 - 0, 509 = 2, 099, \end{matrix}

hasonlóan

\begin{matrix} φ_{H} = {79, 02}^{\circ} = 1, 379, 2 φ_{H} - sin 2 φ_{H} = 2, 384, \end{matrix}

és így az arányszám^{$^{*}$}

\begin{matrix} k = \frac{2, 099 + 0, 9655 \cdot 2, 384}{6, 283} = 0, 70. \end{matrix}

Sopron esetében a

φ_{N} = {70, 06}^{\circ}

és

φ_{H} = {73, 10}^{\circ}

részeredményekből

k = 0, 59

Szeredi Péter (Budapest, Rákóczi F. Gimn., III. o. t.)
Kádas Sándor (Budapest, József A. Gimn., III. o. t.)

^{$^{*}$}

4

számjegyet írtunk ki, bár az adott

f

-értékekben csak

3

értékes számjegy van, és ezért a belőlük számított mértékszámokban sem lehet

3

-nál több helyes számjegy; korai kerekítés esetén azonban a hibák halmozódhatnának.

^{$^{*}$} $2$ értékes számjegyre kerekítve.