Kezdőlap


Feladat:	1455. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Deák Jenő , Domokos László , Kádas Sándor , Szeredi Péter
Füzet:	1967/november, 104 - 107. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Derékszögű háromszögek geometriája, Súlypont, Terület, felszín, Diszkusszió, Síkgeometriai szerkesztések, Feladat
Hivatkozás(ok):	Feladatok: 1966/március: 1455. matematika feladat

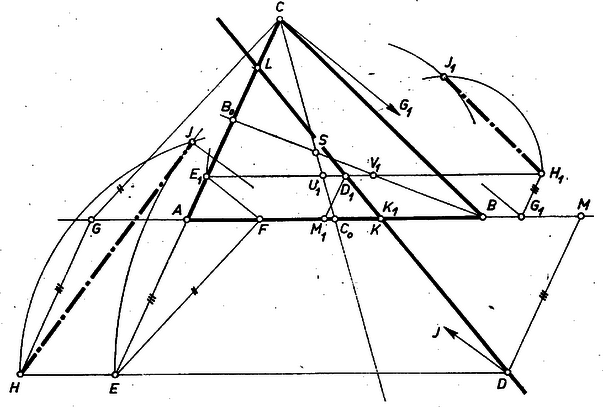
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Legyen először $D$ az $A B C$ háromszögön kívül. Ekkor $E$ a $C A$ meghosszabbításán, $G$ a $B A$ meghosszabbításán, és $H$ a $D E$ meghosszabbításán adódik ( $D$ és $E$ különböző pontok). Így $J$ létrejön, tehát $K$ is, éspedig $A$ -tól $B$ irányában, mert $G K = H J > H D - J D = H D - E D = H E = G A$ . Továbbá a $D K$ egyenes azon az oldalán metszi az $E A$ egyenest egy $L$ pontban, amelyiken $C$ van, mert

\begin{matrix} A K = G K - G A < H D - H E = E D, \end{matrix}

hiszen Thalész tétele szerint

D H J

derékszögű háromszög, és

D H

az átfogója.

Meg fogjuk mutatni, hogy az

A K L

háromszög területe fele akkora, mint az

A B C

háromszögé. Ebből már következik, hogy

L

A C

szakasz belsejében van. Az ellenkező esetben ugyanis az

A K L

háromszög magában foglalná az

A B C

háromszög felét kitevő

A C_{0} C

háromszöget. Továbbá hogy

K

nem lehet

A B

meghosszabbításán, mert akkor

D K

B_{0} B

meghosszabbítását metszené, s így

B_{0}

benne lenne az

E D K

szögtartományban, tehát az

A L

szakaszon, ekkor pedig az

A B C

háromszög felét kitevő

A B B_{0}

háromszög volna az

A K L

háromszög része. Így az

A K L

háromszög része az

A B C

háromszögnek, a szerkesztő eljárás külső

D

pont esetére helyes.
A végzett szerkesztés szerint

A E F

és

A C G

hasonló háromszögek, ezért

\begin{matrix} A G = A F \cdot \frac{A C}{A E} = \frac{A B \cdot A C}{4 \cdot A E} (= E H), \end{matrix}

(1)

hiszen

F

negyedeli az

A B

oldalt. A

D H J

háromszögből

\begin{matrix} G K^{2} & = H J^{2} = D H^{2} - D J^{2} = D H^{2} - D E^{2} = (D H + D E) (D H - D E) = & (2) \\ = (E H + 2 D E) \cdot E H = A G^{2} + 2 D E \cdot A G . \end{matrix}

Messe még az

A C

-vel

D

-n át húzott párhuzamos az

A B

egyenest

M

-ben; ekkor az

A K L

M K D

hasonló háromszög-párból

\begin{matrix} A L = M D \cdot \frac{A K}{M K} = A E \cdot \frac{A K}{M K}, \end{matrix}

(3)

ezért (2), majd (1) felhasználásával

\begin{matrix} A K \cdot A L = A E \cdot \frac{A K^{2}}{M K} = A E \cdot \frac{{(G K - A G)}^{2}}{M G - K G} = & (4) \\ = A E \cdot \frac{A G^{2} + 2 \cdot D E \cdot A G - 2 K G \cdot A G + A G^{2}}{D E + A G - K G} = A E \cdot 2 A G = \frac{A B \cdot A C}{2} . \end{matrix}

(Felhasználtuk, hogy

K

G M

szakaszon van, hiszen

G K = H J < H D = G M

.)
Végül (4)-et

sin B A C

-vel szorozva jobbról az

A B C

háromszög területe áll, balról pedig az

A K L

háromszög területének kétszerese. Ezt akartuk bizonyítani.

II. A

D

pontot a

C_{0} B

szakaszon felvéve az eljárás nem használható,

E

A

-ban adódik, de

G

nem jön létre. (Ekkor azonban

D

játssza

K

szerepét és (4)-et

A D : A C_{0} = A C : A L

alakban írva a vizsgáltnál egyszerűbb szerkesztés adódik:

L

-et

A C

-ből kimetszi a

D C

-vel

C_{0}

-on át fektetett párhuzamos.)

III.

D

-t az

S C_{0} B

háromszögben választva ‐ beleértve az

S C_{0}

S B

szakaszokat is, de

C_{0}

, ill.

B

nélkül ‐ a fenti számítás egyes részei módosulnak. (Az ábra a

D K

egyenes ilyen

D_{1}

pontjából kiindulva is bemutatja a szerkesztést, a megfelelő pontok jele mellett mindenütt 1-es index áll.) Ekkor

G_{1}

A B

félegyenesen adódik, egyébként (1) érvényes.

H_{1}

mindig

E_{1} D_{1}

meghosszabbításán adódik. Legyen ugyanis

C E_{1} = k_{1} \cdot C A

‐ ahol

2 / 3 \leq k_{1} < 1

‐ és messe a

D_{1} E_{1}

egyenes

B_{0} B

-t

V_{1}

-ben,

C C_{0}

-t

U_{1}

-ben, vagyis

D_{1}

U_{1} V_{1}

szakaszon van, megengedve a végpontokat is. Ekkor

\begin{matrix} B_{0} E = (2 k_{1} - 1) \cdot B_{0} A, E_{1} D_{1} \leq E_{1} V_{1} = (2 k_{1} - 1) \cdot A B, \\ A E_{1} = (1 - k_{1}) \cdot C A, A G_{1} = E_{1} H_{1} = \frac{A B}{4 (1 - k_{1})}, \\ E_{1} H_{1} - E_{1} D_{1} \geq E_{1} H_{1} - E_{1} V_{1} = A B (\frac{1}{4 (1 - k_{1})} - (2 k_{1} - 1)) = A B \cdot \frac{1 + {(4 k_{1} - 3)}^{2}}{8 (1 - k_{1})} > 0, \end{matrix}

vagyis

H_{1}

E_{1} V_{1}

meghosszabbításán van.

J_{1}

K_{1}

létrejön, mert

D_{1} H_{1} > E_{1} D_{1}

. Ugyanis

D_{1}

-t az

U_{1} V_{1}

szakaszon mozgatva

E_{1}

G_{1}

H_{1}

állandók, és

D_{1} H_{1}

legkisebb és

E_{1} D_{1}

legnagyobb lehetséges értékének különbsége nem negatív:

\begin{matrix} D_{1} H_{1} - E_{1} D_{1} & \geq V_{1} H_{1} - E_{1} V_{1} = E_{1} H_{1} - 2 E_{1} V_{1} = A B (\frac{1}{4 (1 - k_{1})} - 2 (2 k_{1} - 1)) = \\ = \frac{A B {(4 k_{1} - 3)}^{2}}{4 (1 - k_{1})} \geq 0. & (5) \end{matrix}

(2) így módosul:

\begin{matrix} K_{1} G_{1}^{2} = H_{1} J_{1}^{2} & = D_{1} H_{1}^{2} - E_{1} D_{1}^{2} = (D_{1} H_{1} + E_{1} D_{1}) (D_{1} H_{1} - E_{1} D_{1}) = & (6) \\ = E_{1} H_{1} (E_{1} H_{1} - 2 E_{1} D_{1}) = A G_{1}^{2} - 2 E_{1} D_{1} \cdot A G_{1} . \end{matrix}

(3) változatlanul érvényes. (6) és (1) alapján

\begin{matrix} A K_{1} \cdot A L_{1} = A E_{1} \cdot \frac{A K_{1}^{2}}{M_{1} K_{1}} = A E_{1} \cdot \frac{{(A G_{1} - K_{1} G_{1})}^{2}}{M_{1} G_{1} - K_{1} G_{1}} = \\ = A E_{1} \cdot \frac{A G_{1}^{2} - 2 K_{1} G_{1} \cdot A G_{1} + A G_{1}^{2} - 2 E_{1} D_{1} \cdot A G_{1}}{A G_{1} - E_{1} D_{1} - K_{1} G_{1}} = 2 A E_{1} \cdot A G_{1} = \frac{A B \cdot A C}{2}, \end{matrix}

vagyis a (4) szolgáltatta eredmény változatlanul érvényes. (Felhasználtuk, hogy

G_{1} K_{1}

egy irányú

G_{1} A

-val, vagyis

H_{1} D_{1}

-gyel,

G_{1} M_{1}

-gyel, és hogy

G_{1} M_{1} = H_{1} D_{1} > H_{1} J_{1} = G_{1} K_{1}

.) Ezek szerint a szerkesztés a

C_{0} S B

szögtartomány minden pontjára érvényes, kivéve a

C_{0} B

szakaszt.
(5) szerint speciálisan a

k_{1} = 3 / 4

és

D_{1} = V_{1}

esetben

D_{1} H_{1} = E_{1} D_{1}

, innen

G_{1} K_{1} = H_{1} J_{1} = 0

G_{1} = K_{1}

. Ámde ugyanakkor

A G_{1} = A B

, vagyis

K_{1}

B

-ben adódik, a felező egyenes

B_{0} B

, ami közvetlenül is világos. ‐ Ugyanez várható az

S B

szakaszon levő

D_{1} = V_{1}

pontokra is. Ekkor (6)-ból, (5)-öt felhasználva

\begin{matrix} K_{1} G_{1}^{2} & = E_{1} H_{1} (E_{1} H_{1} - 2 E_{1} V_{1}) = \frac{{(4 k_{1} - 3)}^{2} A B^{2}}{16 {(1 - k_{1})}^{2}}, amiből \\ K_{1} G_{1} = \frac{| 4 k_{1} - 3 | \cdot A B}{4 (1 - k_{1})} & = \frac{(4 k_{1} - 3) \cdot A B}{4 (1 - k_{1})}, ha \frac{3}{4} \leq k_{1} < 1, \\ = \frac{(3 - 4 k_{1}) \cdot A B}{4 (1 - k_{1})}, ha \frac{2}{3} \leq k_{1} < \frac{3}{4} . \end{matrix}

Az első esetben valóban fennáll

\begin{matrix} A K_{1} = A G_{1} - K_{1} G_{1} = A B (\frac{1}{4 (1 - k_{1})} - \frac{4 k_{1} - 3}{4 (1 - k_{1})}) = A B . \end{matrix}

A második esetben viszont csak akkor esik

K_{1}

B

csúcsba, ha

G_{1}

-től nem

A

, hanem

B

felé mérjük fel a

H_{1} J_{1}

szakaszt, hiszen

2 / 3 \leq k_{1} < 3 / 4

esetén már

G_{1}

is az

A B

szakasz pontja, mert

4 (1 - k_{1}) > 1

A G_{1} < A B

. Eszerint az ilyen

D_{1} = V_{1}

ponton át az eljárásunkkal kapott területfelező egyenesen felül más ilyen egyenes is létezik. Ez persze nem hibája eljárásunknak. A vizsgált módon megkapunk egyet a területfelező egyenesek közül.
Szerkesztésünk

S

-ből kiindulva a

C C_{0}

súlyvonalat eredményezi, ugyanis

k_{1} = 2 / 3

esetén

A G_{1} = A B \cdot 3 / 4

és

K_{1} G_{1} = A B / 4

K_{1} = C_{0}

, de a

B B_{0}

, valamint az

A S

súlyvonal is felezi a háromszög területét.
Hasonlóan kimutatható, hogy az

S C_{0}

szakaszon levő

D_{1} = U_{1}

pontokra mindig

K_{1} = C_{0}

adódik.

IV. A sík minden pontja beletartozik egyikébe annak a 6 szögtartománynak, melyek közös csúcsa

S

, és amelyeket a 3 súlyvonal félegyenesei határolnak. A további ilyen

D

pontok esetében úgy válik eljárásunk alkalmassá és a fentiek szerint érvényessé, hogy minden előforduló

A

B

C

betű helyére egy más sorrendjüket írjuk; ha pl. a

B_{0} S A

szögtartományban van

D

, akkor

A

B

C

helyére rendre

C

A

B

írandó. ‐

D

bizonyos helyzeteiben az eredeti betűzés szerinti szerkesztés is megadja a területfelező egyenesnek az

A B

egyenesen levő pontját, ha a

H J

szakasz felmérési irányát alkalmasan módosítjuk, ennek vizsgálatát azonban itt nem tekintjük feladatunknak.

V. Csekély végrehajtási egyszerűsítés adódik abból az észrevételből, hogy a

D

E

H

ponthármas eltolással átvihető

M

A

G

-be. Ha

H

helyett

M

-et szerkesztjük, az

M G

átmérő fölé írjuk a Thalész-kört, ebből az

M

körüli,

M A

sugarú körívvel metsszük ki

J^{*}

-ot, végül ezt

G

körül ráfordítjuk

A B

-re, a

K

pontba, ez csak annyival kevesebb az előírt szerkesztésnél, hogy a 7. lépésben nem kell átemelni a körző csúcsát

H

-ból

G

-be.