Kezdőlap


Feladat:	1453. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Domokos László , Herényi István , Szeredi Péter
Füzet:	1967/március, 100 - 102. oldal		PDF \| MathML
Témakör(ök):	Euler-egyenes, Körülírt kör, Súlypont, Magasságpont, Síkgeometriai számítások trigonometria nélkül háromszögekben, Diszkusszió, Háromszögek szerkesztése, Feladat
Hivatkozás(ok):	Feladatok: 1966/március: 1453. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ismeretes, hogy a háromszög $M$ magasságpontja, $S$ súlypontja és $k$ körülírt körének $K$ középpontja ebben a sorrendben a háromszög Euler-féle egyenesén van, és $M S = 2 S K$ . Ennek alapján $M$ -et és $S$ -et az előírt távolságban felvéve, kijelölhetjük $K$ helyzetét, és az adott $r$ sugár alapján megrajzolhatjuk 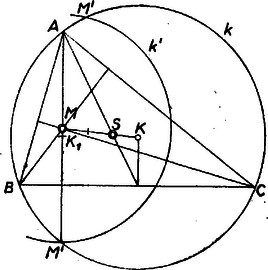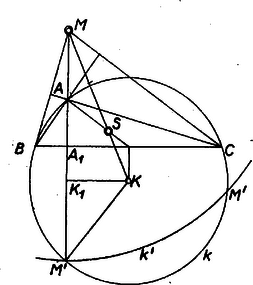$k$ -t.

1. ábra

2. ábra

Tudjuk másrészt, hogy

M

-nek bármelyik oldal egyenesére való tükörképe rajta van

k

-n, és azonos az oldalra merőleges

m

magasságegyenes és

k

második, a szemben fekvő csúcstól különböző közös pontjával, ha pedig

m

érinti

k

-t, akkor azonos a csúccsal. Tekintsük

M

tükörképét arra az oldalegyenesre, amelyiknek

M

-től való

d

távolsága adott, legyen a kép

M'

. Így

M M' = 2 d

, tehát

M'

-t kimetszi

k

-ból az

M

körül

2 d

sugárral írt

k'

kör. Most már a kérdéses oldal egyenesét megadja

M M'

felező merőlegese, az oldal végpontjait ennek

k

-n levő metszéspontjai, a harmadik csúcsot pedig az

M M'

magasságegyenesnek

k

-val való második metszéspontja (az

1

‐

2

. ábrán

B

és

C

, ill.

A

), amennyiben pedig

M M'

érinti

k

-t, akkor

A

azonos

M'

-vel 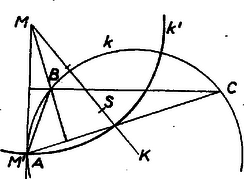(3. ábra).

3. ábra

Csak azt kell bizonyítanunk, hogy az

A B C

háromszög magasságpontja

M

. Nem lehet, hogy a magasságpont az

A M'

magasságegyenesnek egy az

M

-től különböző pontja legyen, mert annak

B C

-re való tükörképe nem

M'

lenne.

K

és

k

egyértelműen megszerkeszthetők.

M'

létrejön, ha

k'

-nek van közös pontja

k

-val, azaz ha

\begin{matrix} | 2 d - r | ≦ e ≦ 2 d + r, \end{matrix}

(1)

ahol

e = M K = 3 M S / 2

. ‐

M M'

felező merőlegese létrejön, ha

M'

M

-től különböző pont, azaz

d > 0

. Ezt most feltesszük, a

d = 0

esetre később visszatérünk. ‐

B

C

létrejön, ha a felező merőlegesnek

K

-tól való távolsága kisebb

r

-nél. Ez mindenesetre teljesül, ha

K

-nak

M M'

-n levő

K_{1}

vetületére nézve

M K_{1} ≦ M' K_{1}

. Különben (2. ábra)

M M'

-nek

A_{1}

felezőpontja elválasztja

K_{1}

-et

M

-től, és a kérdéses távolság

A_{1} K_{1}

. A

K K_{1} M

és

K K_{1} M'

derékszögű háromszögekből (tekintet nélkül

K_{1}

-nek az

A_{1} M'

félegyenesen elfoglalt helyzetére)

\begin{matrix} M K_{1}^{2} = e^{2} - K K_{1}^{2} = e^{2} - r^{2} + M' K_{1}^{2}, \\ {(d + A_{1} K_{1})}^{2} = e^{2} - r^{2} + {(d - A_{1} K_{1})}^{2}, \end{matrix}

és így a feltétel:

\begin{matrix} A_{1} K_{1} = \frac{e^{2} - r^{2}}{4 d} < r, amiből e < \sqrt[]{4 d r + r^{2}} = \sqrt[]{r (r + 4 d)} . \end{matrix}

(2)

Itt

e

(el sem érhető) fölső korlátja kisebb (1) jobb oldalánál, ezért a két feltétel így egyesíthető:

\begin{matrix} | 2 d - r | ≦ e < \sqrt[]{r (r + 4 d)} . \end{matrix}

(3)

Végül

A

mindenesetre létrejön, mert

M'

k

-n van. ‐ A két

M'

metszéspontból adódó két háromszög egymás tükörképe az

M S

egyenesre.

k

és

k'

érintkezése esetén egyenlő szárú háromszöget kapunk.

4. ábra

d = 0

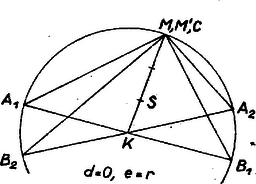esetben a fenti felező merőleges határozatlan. Ez az eset azt jelenti, hogy

M

rajta van a háromszög szóban forgó oldalán. Ismeretes azonban, hogy

M

csak derékszögű háromszögben esik a háromszög kerületére; mégpedig a derékszög csúcsába, ekkor tehát rajta van

k

-n is,

M K = e = r

. Ha ez teljesül, akkor minden

A B M

háromszög megfelel, ahol

A

B

k

egy átmérőjének végpontjai, és

M

-től különbözők. (Más szóval :

M M'

felezőpontja maga

M

, minden ezen átmenő és

M K

-tól különböző egyenes vehető

M B

azaz

C B

felező merőlegeseként, és

C A ⊥ C B,

4. ábra.) Ha viszont

d = 0

és

e \neq r

, akkor nincs megoldás.
Külön említendő az

e = 0

eset is, vagyis ha

M

és

S

egybeesnek, és így

K

is. Ekkor a (3) feltétel szerint csak

2 d = r

esetén van megoldás. Ekkor

k'

azonos

k

-val,

M'

k

tetszés szerinti pontja lehet, mindig szabályos háromszöget kapunk.

Domokos László (Tatabánya, Árpád Gimn., IV. o. t.),
Herényi István (Budapest, I. István Gimn., IV. o. t.),
Szeredi Péter (Budapest, Rákóczi F. Gimn., III. o. t.)
dolgozatai alapján, kiegészítésekkel