Feladat:	1452. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bajna Zsolt ,  Bottyán I. ,  Deák J. ,  Domokos L. ,  Fencsik G. ,  Fialovszky Béla ,  Hámori Veronika ,  Havas J. ,  Medveczky M. ,  Muraközy Gy. ,  Szentgáli Á. ,  Szeredi P. ,  Szilágyi Péter
Füzet:	1967/április, 151 - 156. oldal		PDF  |  MathML
Témakör(ök):	Egyenlőtlenségek, Kocka, Terület, felszín, Térfogat, Feladat
Hivatkozás(ok):	Feladatok: 1966/március: 1452. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.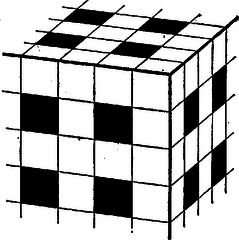     1. ábra   I. megoldás. $a)$ Állítsunk mindegyik felhasznált osztóponton át merőleges síkot az illető élre. Az egy élre merőleges síkok a kockát $k$ számú, valamelyik kockalappal párhuzamos rétegre osztják, és a többi síkok ezeket $k^3$ számú, $1/k$ élhosszúságú, ${1/k}^3$ térfogatú kisebb kockára. Nyilvánvaló, hogy minden ilyen kis kockát a maga egészében vagy eltávolítunk, vagy nem, ezért a térfogat megállapítása a megmaradó kis kockák összeszámlálásában áll. 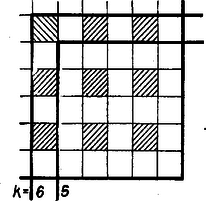 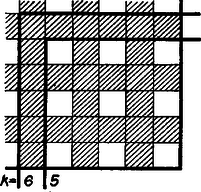   2. ábra     3. ábra   A számlálást vízszintes rétegenként végezzük. A páratlan sorszámú rétegek egybevágók egymással (2. ábra), ugyanígy a páros sorszámúak is egymás között (3. ábra), ugyanis az előbbieken az eltávolítandó hasábok közül csak az állók haladnak át ‐ bányászati hasonlattal: az aknák ‐, hiszen az e rétegek palástján levő eredeti kis négyzetek két sorszáma közül legföljebb egy páros. A páros sorszámú rétegekben viszont elölről hátrafelé és jobbról balra is haladnak fekvő eltávolítandó hasábok ‐ vágatok ‐ , mindegyiken egyformán a palást előlapjának, ill. jobb oldallapjának minden második kis négyzetéből kiindulva. A páratlan sorszámú rétegekből csak azok a kis kockák távolítandók el, amelyeknek elölről és jobbról számított sorszáma páros, a páros sorszámúakban viszont csak azok maradnak meg, amelyeknek e két sorszáma páratlan. Legyen a $k$-nál nem nagyobb páros természetes számok száma $i$. Így a $k-i$ számú páratlan réteg mindegyikében $k^2-i^2$ kocka marad, az $i$ számú páros rétegben pedig egyenként ${\left(k-i\right)}^2$ kocka, így a maradó test térfogata $\begin{array}{c}{\displaystyle V=\left[\left(k-i\right)\left(k^2-i^2\right)+i{\left(k-i\right)}^2\right]\cdot \frac{1}{k^3}=\frac{{\left(k-i\right)}^2\left(k+2i\right)}{k^3}\mathrm{.}}\end{array}$ (1) Páros $k$ esetén, $i=k/2$, páratlan $k$ esetén $i=\left(k-1\right)/2$, ezért $\begin{array}{c}{\displaystyle V_{\text{ros}}=\frac{1}{2}\mathrm{,}{V}_{\text{tlan}}=\frac{{\left(k+1\right)}^2\left(2k-1\right)}{4k^3}=\frac{1}{2}+\frac{3k^2-1}{4k^3}\mathrm{.}}\end{array}$ Ezek szerint a térfogat bármely páros $k$ szám esetén ‐ és csak ekkor ‐ nem nagyobb $1/2$-nél. $b)$ Nyilvánvaló, hogy a maradó test határfelülete csupa kis $1/k$ oldalú, $1/k^2$ területű négyzetből áll, ezeket fogjuk megszámlálni. Két kis kocka közös határlapja akkor tartozik a maradó test belső határfelületéhez, ha egyiküket eltávolítottuk, a másikat nem; nevezzük ezeket $h$ négyzeteknek. Az ilyen lapokat elég a nagy kocka vízszintes metszeteiben megszámlálnunk, mert az előlappal, valamint a jobb oldallappal párhuzamos metszetekben számuk ugyanennyi, hiszen a kockát a jobb felső elülső csúcsból kiinduló testátlója körül ${120}^{\circ }$-kal bármelyik irányban elfordítva, az önmagával fedésbe jut, és ez áll a maradó testre is. Ugyanezért a kocka lapjai közül is elég megállapítani a fedő- és az alaplap maradó részének területét. 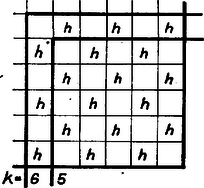    4. ábra   A $k-1$ közbülső síkmetszet mindegyikében ugyanannyi $h$ négyzet van, mert mindegyik síkmetszet egy páros és egy páratlan sorszámú réteg közös határlapja. $h$-négyzet az olyan, amelynek kockáját a 2. ábra megmaradónak, a 3. ábra pedig eltávolítottnak jelöli (4. ábra). Az előlaptól számított sorszámuk páratlan ‐ a páratlan sorszámú réteg miatt (2. ábra) ‐ , a jobb oldallaptól számított sorszám pedig páros ‐ a páros sorszámú réteg miatt (3. ábra) ‐ , vagy fordítva. Mindkét esetben $i$ sor mindegyikében $k-i$ négyzetet találunk, így a vízszintes metszetekben a $h$ négyzetek száma $\begin{array}{c}{\displaystyle 2i\left(k-i\right)\left(k-1\right)\mathrm{.}}\end{array}$ (2) A fedőlapon annyi kis négyzet marad, mint ahány kis kocka van az első rétegben, és ugyanennyi az alaplapon is, amennyiben $k$ páratlan. Ekkor tehát a maradó test felszíne: $\begin{array}{c}{\displaystyle F_{\text{tlan}}=3\left\{2\frac{k-1}{2}\cdot \frac{k+1}{2}\left(k-1\right)+2\cdot \left[k^2-{\left(\frac{k-1}{2}\right)}^2\right]\right\}\cdot \frac{1}{k^2}=\frac{3{\left(k+1\right)}^2}{2k}\mathrm{.}}\end{array}$ (3) Páros $k$ esetén viszont az alaplapon annyi kis négyzet marad, ahány kis kocka van az alsó rétegben, ezért $\begin{array}{c}{\displaystyle F_{\text{<span style="font-weight: normal;font-style: normal;">ros</span>}}=3\left[2\cdot \frac{k}{2}\cdot \frac{k}{2}\left(k-1\right)+\left(k^2-\frac{k^2}{4}\right)+{\left(\frac{k}{2}\right)}^2\right]\cdot \frac{1}{k^2}=\frac{3}{2}\left(k+1\right)\mathrm{.}}\end{array}$ (4) Az $F>\mathrm{100,}$ azaz $F-100>0$ követelményből páratlan $k$ esetén: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{3{\left(k+1\right)}^2-200k}{2k}=\frac{3}{2k}\left(k^2-\frac{194}{3}k+1\right)=\frac{3}{2k}\left[{\left(k-\frac{97}{3}\right)}^2-\frac{9400}{9}\right]>\mathrm{0,}}\hfill \\ \hfill {\displaystyle k>\frac{97}{3}+\frac{\sqrt[]{9400}}{3}>64;}\hfill \end{array}}$ páros $k$ esetén pedig: $\begin{array}{c}{\displaystyle \frac{3\left(k+1\right)-200}{2}>\mathrm{0,}\text{<span style="font-weight: normal;font-style: normal;">azaz</span>}k>\mathrm{65,}}\end{array}$ tehát $k\geqq 65$ esetén mindenképpen teljesül $F>100$, a test felszíne meghaladja az eredeti kocka felszínének $16$-szorosát (szivacsosság).    Fialovszky Béla (Esztergom, Temesvári Pelbárt Ferences g. III. o. t.)  Bajna Zsolt (Esztergom, Bottyán J. Műszerip. t. IV. o. t.)   Megjegyzés. Eredményünk $k=1$ esetén is megadja a helyes, várható $V=1$, $F=6$ értéket.   II. megoldás. $a)$ Más meggondolással vezetjük le a fenti (1)‐(2) kifejezéseket. Az aknákban egyenként $k$, együttesen $i^2\cdot k$ kis kockát távolítunk el. Ugyanennyit távolítanánk el a teljes kockából pl. a hátrafelé menő vágatokban is. Az aknák előzetes eltávolítása után viszont egy-egy vágat már $k$-nál kevesebb kis kockát tartalmaz. Ha egy kis kockán két vágat halad át, akkor akna is megy át rajta (2.‐3. ábra), hiszen az első kettő miatt már mindhárom irányú rétegezés szerint páros sorszámú rétegbe tartozik. Eszerint $i^3$ számú kis kocka mindegyikét $3$-szor kellene eltávolítanunk. A többi eltávolítandó kocka csak egy aknába vagy vágatba tartozik bele. Eszerint az aknák $i^{2}k-i^{3}1$-szer eltávolítandó kis kockát tartalmaznak, az egyes vágatok is, tehát az eltávolítandó kis kockák együttes száma, majd a térfogat 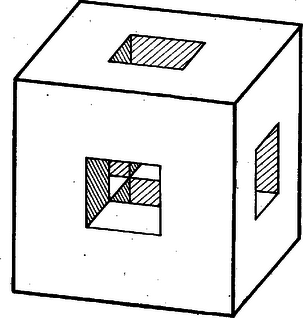$\begin{array}{c}{\displaystyle i^3+3\left(i^{2}k-i^3\right)\mathrm{,}V=\left[k^3-i^3-3\left(i^{2}k-i^3\right)\right]\cdot \frac{1}{k^3}\mathrm{,}}\end{array}$ ami azonos (1)-gyel.     5. ábra   $b)$ Az I. megoldás szerinti kis $h$-négyzetek mindegyike mentén $1$-szer eltávolítandó kis kocka csatlakozott a maradó testhez, hiszen a $3$-szor eltávolítandó kockák minden szomszéd kockáját is eltávolítottuk. A $3i^2\left(k-i\right)$ számú $1$-szer eltávolított kis kocka helyén általában egy kis alagút marad hátra (5. ábra), melynek határfalát $4$ kis $h$ négyzet alkotja. (Két szemben fekvő lapjával $3$-szor eltávolítandó kis kockához csatlakozik, vagy $1$ lapjával ilyenhez, a szemben fekvővel pedig a nagy kocka lapjához; az ábrán, $k=3$ esetében csak ilyenek vannak.) Páratlan $k$ esetén csak ez lehetséges, így a belső határfelület kis négyzeteinek száma $4\cdot 3\cdot i^2\left(k-i\right)$, ami $i=\left(k-1\right)/2$ figyelembevételével azonos a (2) kifejezés $3$-szorosával. 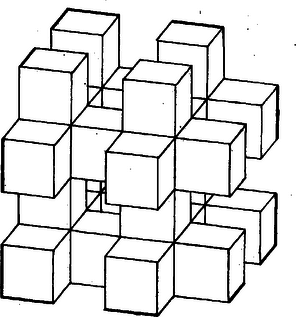    6. ábra   Páros $k$ esetén egyes $1$-szer eltávolított kis kockák helyén nem jön létre a mondott zárt alagút, éspedig az alsó, a hátsó és a bal szélső rétegben, mert a létrehozó akna, vágat egyik fala a nagy kocka lapsíkjába esik (6. ábra, $k=4$, a testet úgy fordítottuk át, hogy bal alsó hátsó csúcsa a jobb felső elülső helyére jusson). Az alagutak megfelelő $1-2$ négyzetlapját (2) új előállításában a $4\cdot 3\cdot i^2\left(k-i\right)=3k^3/2$ számból mellőznünk kell, hiszen a test külső határfelületének, részeként (4)-ben pl. az alsó lapban kerülnek beszámításra. A mondott rétegekben $i^2=k^2/4$ kis kocka marad vissza, ugyanennyi a $3$-szor eltávolítandók száma, ezért a bennünket most érdeklő kockák száma mindegyik határrétegben $k^2/2$. $3$-szor ennyi kis négyzet-határlap adódik külsőnek, és a $3k^3/2-3k^2/2=3k^2\left(k-1\right)/2$ különbség $i=k/2$ figyelembevételével páros $k$ esetére is kiadja (2)-nek $3$-szorosát. A további számítás azonos az I. megoldásbelivel.    Szilágyi Péter (Budapest, Kossuth Zs. g. IV. o. t.)  Hámori Veronika (Budapest, Ságvári E. gyak. g. III. o. t.)   III. megoldás. $a)$ (1)-re elvezet a következő meggondolás is. Egy kis kocka helyzetét három, $k$-nál nem nagyobb természetes szám írja le, ezek azt mutatják, hogy a $3$ egymásra merőleges irányban hányadik rétegbe esik a kis kocka. Azok a kis kockák maradnak meg, amelyekhez tartozó számhármasban legfeljebb egy páros szám van. Azoknak a kis kockáknak a száma, amelyek helyzetét $3$ páratlan szám írja le, ${\left(k-i\right)}^3$, azoké, amelyek első, második, ill. harmadik jelzőszáma páros, a többi páratlan, egyenként ${i\left(k-i\right)}^2$, így a visszamaradó kockák száma ${\left(k-i\right)}^3+3i{\left(k-i\right)}^2=\left(k+2i\right){\left(k-i\right)}^2\mathrm{.}$ $b)$ A felszínhez eljutunk a kis négyzetlapok alábbi csoportosításával is. A keletkezett test felületéhez tartozik minden olyan kis kockának legalább $4$ határlapja, amelyiknek helyzetét egy páros és két páratlan szám jelöli, mert abban az őt tartalmazó rétegben, amelyiknek a sorszáma páros, a kiszemelt kis kockával szomszédos $4$ kis kockát vagy eltávolítottuk, vagy nem is volt mellette kis kocka, mert a nagy kocka egy lapja határolta (7. ábra, a rétegek kissé széthúzva). A maradó $2$ oldalról viszont csupa páratlan számmal jellemzett, tehát a visszamaradt testhez tartozó kis kocka csatlakozik, kivéve ha kis kockánk az utolsó rétegben van (tehát $k$ páros). Az ilyen határlapokat külön fogjuk összeszámolni. Az így tekintetbe vett kis kockák száma $3i{\left(k-i\right)}^2$, a határlapok felszíne pedig: 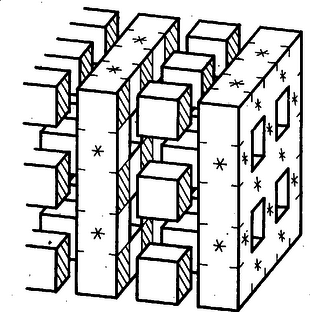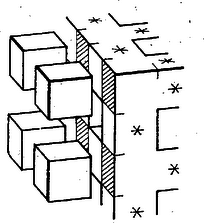$F_1=3\cdot 4\cdot i{\left(k-i\right)}^2/k^2$.     7. ábra     8. ábra   Távolítsuk el most mindezeket a kis kockákat (vagyis a 7. ábra ${}^{*}$ jelű kis kockáit is), és a visszamaradókat toljuk össze az élekkel párhuzamos irányokban. Ezzel csak olyan lapok kerültek egymással fedésbe, amelyek korábban sem tartoztak a test felszínéhez, és az ilyenek sehol sem váltak határlappá, kivéve ha $k$ páros és az utolsó rétegből távolítottunk el egy kis kockát. Ezzel egy kis kocka egy határlapja, ami korábban a testnek nem volt határlapja, azzá vált, viszont az eltávolított kis kockának egy ötödik, eddig számításon kívül hagyott lapja a test felszínéhez tartozott (8. ábra). Így ,,szivacsos'' testünk felszínét megkapjuk, ha $F_1$-hez hozzáadjuk a most keletkezett test felszínét. Ez már egy tömör kocka, amelyiknek élhossza $\left(k-i\right)/k$, tehát felszíne: $\begin{array}{c}{\displaystyle F_2=6{\left(\frac{k-i}{k}\right)}^2\mathrm{,}\text{<span style="font-weight: normal;font-style: normal;">és így</span>}F=F_1+F_2=\frac{{\left(k-i\right)}^2}{k^2}\left(2i+1\right)\mathrm{.}}\end{array}$ Ha $k$ páros, akkor $i=k/2$, $2i+1=k+1$; ha $k$ páratlan, akkor $i=\left(k-1\right)/2$, $2i+1=k$, így $\begin{array}{c}{\displaystyle F_{\text{<span style="font-weight: normal;font-style: normal;">ros</span>}}=\frac{3}{2}\cdot \left(k+1\right)\mathrm{,}{F}_{\text{<span style="font-weight: normal;font-style: normal;">tlan</span>}}=\frac{3}{2}\cdot \frac{{\left(k+1\right)}^2}{k}\mathrm{.}}\end{array}$