|
| Feladat: |
1447. matematika feladat |
Korcsoport: 16-17 |
Nehézségi fok: átlagos |
| Megoldó(k): |
Bárány I. , Baróthy B. , Bod Judit , Bottyán I. , Deák Jenő , Domokos L. , Fencsik Gábor , Fialovszky B. , Fövényesi Ildikó , Gáspár A. , Havas J. , Herényi István , Inczédy János , Joó I. , Kádas S. , Kafka P. , Kloknicer J. , Kottra G. , Králik I. , Langer T. , Lévai F. , Medgyesy K. , Pethő I. , Pintér J. , Sebő I. , Sólymos L. , Szeidl L. , Szentgáli Á. , Szeredi Péter , Sziklai P. , Szilágyi P. , Tolnay-Knefély T. , Varsányi Anikó , Verdes S. , Zambó Péter |
| Füzet: |
1967/január,
12 - 15. oldal |
 PDF | PDF |  MathML MathML |
| Témakör(ök): |
Háromszögek hasonlósága, Forgatva nyújtás, Magasságpont, A háromszögek nevezetes pontjai, Diszkusszió, Háromszögek szerkesztése, Síkbeli szimmetrikus alakzatok, Feladat |
| Hivatkozás(ok): | Feladatok: 1966/február: 1447. matematika feladat |
|
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás. Válasszuk a betűzést úgy, hogy a keresett háromszög oldalának felezőpontja az adott pont, a és magasságainak talppontjai közti szakasz felezőpontja az adott pont, és metszéspontja pedig legyen .
és rajta van a átmérő fölötti, középpontú Thalész-körön, ezért a háromszög egyenlő szárú, súlyvonala egyben magassága is, tehát merőlegesen áll -re (1. és 2. ábra).
A és háromszögek első két-két szöge rendre egyenlő, mert ugyanazon ívein nyugvó kerületi szögek, így a két háromszög hasonló. Ezekben és egymásnak megfelelő súlyvonalak, ezért | | (1) |
Eszerint a derékszögű háromszög megszerkeszthető ismert befogójából, valamint másik befogójának és átfogójának ismert arányából a következő lépésekben: -n át merőleges egyenest állítunk -re, erre (bármelyik irányban) fölmérjük a szakaszt, az körüli sugarú körívvel kimetsszük a egyenes pontját, és -n át párhuzamost húzunk -val, ennek -vel való metszéspontja . Vesszük -nek -re való tükörképét, megrajzoljuk az és magasságegyeneseket és a talpponton át rájuk merőlegesen az , oldalegyéneseket, ezek metszéspontjai adják az csúcsokat. 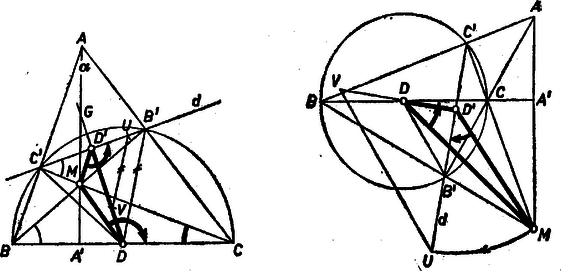 1. ábra
A szerkesztés szerint a háromszög hasonló -hoz, ezért megfelel (1)-nek; az háromszögnek a magasságpontja, és felezi a talppontok közti szakaszt. Azt kell csak bizonyítanunk, hogy a kapott oldal felezőpontja azonos az adott ponttal. Az elemzés szerint a húrnégyszög köré írt kör középpontja, ezért rajta van felező merőlegesén, akárcsak is rajta van, a szerkesztésnél fogva. Továbbá ismét az elemzésnél fogva -nak -től és -től mért távolságaira teljesül (1), és szerkesztése folytán teljesül -re és -re is. Így azonos -vel.
A szerkesztés egyértelműen végrehajtható, ha és különbözők, (különben nem jön létre; ez a feltétel és egybeesését is kizárja), végül ha sem esik egybe -mel. Egybeesésük esetén ugyanis oda esik és is, a háromszög -nál derékszögű, de határozatlan, a körüli sugarú kör bármely átmérője lehet átfogója (kivéve a -ből kiinduló átmérőt).
Akkor is derékszögű háromszöget kapunk ‐ de egyértelműen ‐, ha merőleges -re, mert ekkor -be esik , és így is; könnyű belátni ugyanis, hogy csak derékszögű háromszögben esik a háromszög kerületére, és ekkor éppen a derékszög csúcsába.
Megemlítjük még a következőket: Ha ugyanazon az oldalán van -nek, mint , akkor hegyesszögű háromszög adódik, ha pedig a másik oldalán, akkor a háromszög valamelyik szöge tompaszög. Ha egy egyenesbe esnek, egyenlő szárú háromszöget kapunk.
Szeredi Péter (Budapest, II. Rákóczi F. g. III. o. t.) és
Fencsik Gábor (Budapest, Berzsenyi D. g. III. o. t.)
Megjegyzések. 1. A szerkeszthetőség ‐ másképpen ‐ feltételére egyszerű értelmezés adható, felhasználva (1)-et és az és háromszögek hasonló voltát (lásd III. megoldás): | |
különben nem létezik.
2. -t és -t -ből kimetszhetjük a és alappontokhoz és a arányhoz tartozó Apollóniosz-körrel is. E kör egy átmérőjének végpontjait a egyenesből a háromszög -ből kiinduló belső és külső szögfelezője metszi ki.
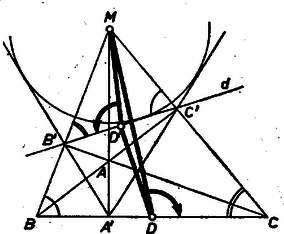 2. ábra II. megoldás. (vázlat). Az és háromszögek fent kimondott hasonlóságához hozzátesszük, hogy tükrösen hasonlók, csúcsaikat a fenti sorrendben, a páronkénti megfelelés rendjében körüljárva ellentétes irányú körüljárásokat kapunk (1‐2. ábrák 3 esete). Tükrösen hasonlók e két háromszögnek a megfelelő súlyvonalak két oldalán levő részei is, pl. az és háromszögek, ezért , és forgásirányuk ellentétes (a megfelelő félegyenesek mindig a egyenes ugyanazon oldalán vannak). Ennek alapján a és egyenesek közti egyik szögnek a félegyenes mellé való alkalmas átmásolásával megkapjuk a egyenest. vetülete ezen az -ból húzott magasság talppontja.
Felhasználjuk még, hogy a (nem derékszögű) háromszöghöz tartozó talpponti háromszög egyik érintő körének középpontja . Abból adódik ez, hogy a talpponti háromszög belső és külső szögeinek felezői az eredeti háromszög oldalegyenesei és magasságegyenesei.Az közepű érintő kör az I. megoldásbeli oldalegyeneshez megszerkeszthető, a hozzá -ből húzott két érintő a talpponti háromszög további két oldalegyenese, -ből kimetszik -t, -t, tovább az I. megoldás szerint haladhatunk.
Az elemzésben csak vázolt állítások és a szerkesztés helyessége bizonyítását, valamint a diszkussziót az olvasóra kell hagynunk.
Inczédy János (Vác, Sztáron S. g. II. o. t.)
Megjegyzés. Az, hogy és tükrösen hasonlók, azt jelenti, hogy az utóbbi háromszög pl. egy alkalmas középpontú nyújtással (vagy összehúzással) az előbbivel egybevágó, tükrös helyzetű háromszögbe vihető át. Így a egyenes irányát megkaphatjuk, ha -t pl. az egymásnak megfelelő és irányok szögfelezőjére tükrözzük.
Herényi István (Budapest, I. István g. IV. o. t.)
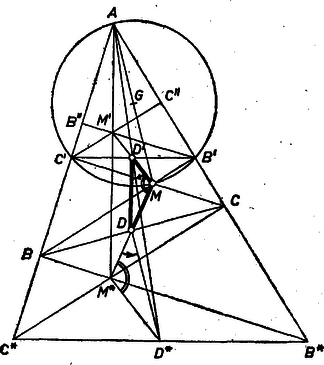 3. ábra
III. megoldás (vázlat). Elsőnek az csúcsot szerkesztjük meg. Legyen tükörképe -re (3. ábra), Így paralelogramma, , ezért , ugyanígy , tehát az háromszög magasságpontja. és hasonló háromszögek (lásd az 1‐2. ábrákat is), mert -nál levő szögük vagy közös vagy csúcsszöge egymásnak, továbbá -nél és -nél levő szögük a kerületi szögek tétele szerint egyenlő. A csúcsoknak a mondott sorrend szerinti körüljárása ellentétes irányú, hiszen a vesszős csúcsok az -nál levő szög másik száregyenesén vannak, vagy mindkettő azon az oldalán -nak, mint és vagy ( esetén) mindkettő a csúcsszög szárain. (A tükrös hasonlóság tengelye a szög felezője:)
Legyen tükörképe -re , és messe a egyenes -t -ban, az -t -ban. Így paralelogramma, és , , az háromszög magasságpontja. Ebből a háromszögből ugyanúgy keletkezik , mint -ből , tehát is ellentétes körüljárással hasonló -höz, ennélfogva azonos körüljárással hasonló az háromszöghöz. Mivel csúcsuk közös, és itt fut össze és , azért és az középpontra nézve hasonló helyzetűek is. Eszerint átmegy -n, és ugyanez áll a oldal felezőpontját -vel összekötő egyenesre, hiszen a hasonló helyzetű háromszögek megfelelő pontjait összekötő egyenesek átmennek a hasonlóság középpontján. Eszerint elég -t megszerkeszteni. Ez két szögmásolással adódik abból, hogy háromszög az utóbbi hasonlóságban a háromszög megfelelője, és ezek is ellentétes körüljárásúak; ezért , az félegyenes párhuzamos és ellentétes irányú -vel, továbbá , és forgási irányuk ellentétes.
ismeretében az átmérő fölötti Thalész-körrel -ből kimetszhetjük -t és -t, és tovább az I. megoldás szerint haladhatunk. Felhasználhatjuk azt is, hogy -nek felezőpontja az háromszög Feuerbach-körének -vel átellenes pontja (ugyanis az magasság talppontja is rajta van ezen a körön, és ), ezért a D átmérőjű körrel is kimetszhetők a pontok. Vagy az -re -n át állított merőlegesben megkaphatjuk a egyenest (II. megoldás).
A bizonyítást és a diszkussziót hely hiányában az olvasóra kell hagynunk.
Deák Jenő (Budapest, Kölcsey F. g. IV. o. t.)
Tompaszögű háromszög esetére lásd a szögek számítását pl. gyakorlatban, K. M. L. 32 (1966) 66. o. |
|
 PDF |
PDF |  MathML
MathML 

