Kezdőlap


Feladat:	1446. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Argyelán J. , Balna Zs. , Bárány I. , Barcza Gyöngyi , Bottyán I. , Csirmaz L. , Cziffra A. , Deák Jenő , Domokos L. , Faur T. , Fencsik G. , Gáspár András , Halek T. , Hámori Veronika , Iváncsy Sz. , Juhász Ágnes , Kádas S. , Kafka P. , Medgyesy K. , Palla T. , Papp E. , Pintér J. , Pintz J. , Recski A. , Solymosi A. , Sugár L. , Szabó Klára , Szeidl L. , Szentgáli Á. , Szeredi P. , Szilágyi I. , Szilágyi P. , Takács Ágnes , Tiszai I. , Tolnay-Knefély T. , Varsányi Anikó , Verdes S.
Füzet:	1967/április, 156 - 158. oldal		PDF \| MathML
Témakör(ök):	Trigonometriai azonosságok, Terület, felszín, Paralelogrammák, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1966/február: 1446. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Elég azzal az esettel foglalkozni, ha $N_{0}$ oldalai különbözők, hiszen rombuszból kiindulva már $N_{1}$ is ponttá, az átlók metszéspontjává zsugorodik össze, és az állítás semmitmondóvá válik. Válasszuk a betűzést úgy, hogy $A B = a > A D = b$ , és $B A D ∢ = α ≦ A B C ∢$ legyen (1. ábra).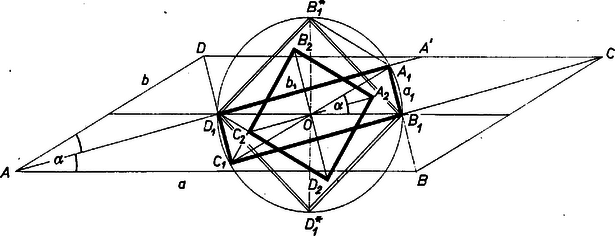

1. ábra

Jelöljük

A_{1}

B_{1}

C_{1}

D_{1}

betűvel

N_{1}

-nek rendre azt a csúcsát, ahol az

A B

B C

C D

D A

oldal végpontjaiból kiinduló szögfelezők metszik egymást. Megmutatjuk, hogy az

N_{1}

négyszög téglalap, az átlói közti kisebb szög

α

, és átlóinak hossza

a - b

. Ugyanis az

N_{0}

szomszédos csúcsaiból kiinduló szögfelezők merőlegesek egymásra, mert pl. az

A D D_{1}

háromszög

D_{1}

-nél levő külső szöge egyenlő a

C D A

és a

D A B

szög felének összegével, ez pedig

90^{\circ}

D_{1}

egyenlő távol van az

A

-ból és

D

-ből kiinduló oldalaktól, tehát rajta van

N_{0}

-nak

A B

-vel párhuzamos középvonalán. Ugyanez áll

B_{1}

-re, mert ez

D_{1}

tükörképe

N_{0}

-nak

O

középpontjára nézve, tehát a

B_{1} D_{1}

átló párhuzamos

A B

-vel; hasonlóan

A_{1} C_{1} ∥ A D

, ezek szerint

O

N_{1}

-nek is középpontja. ‐ A mondott középvonalnak

D_{1}

és az

A D

oldal közé eső szakasza az

A D A'

háromszög középvonala ‐ ahol

A'

A D_{1}

szögfelező metszéspontja a

C D

oldallal ‐, így a hossza

D A' / 2 = b / 2

, ezért

B_{1} D_{1} = a - b

; továbbá

B_{1} O A_{1} ∢ = α

.
Bizonyításunkban

N_{0}

és

N_{1}

helyére

N_{1}

-et, ill.

N_{2}

-t írva, azt kapjuk, hogy

N_{2}

olyan téglalap, amelyben az átlók közti szögek egyenlők az

N_{1}

csúcsainál levő szögekkel ‐ vagyis

N_{2}

négyzet ‐, az átlók hossza pedig egyenlő

N_{1}

oldalai különbségének abszolút értékével:

A_{2} C_{2} = | a_{1} - b_{1} |

. Így

N_{2}

területe:

\begin{matrix} t_{2} = \frac{A_{2} C_{2}^{2}}{2} = \frac{{(a_{1} - b_{1})}^{2}}{2} = \frac{a_{1}^{2} + b_{1}^{2}}{2} - a_{1} b_{1} = \frac{A_{1} B_{1}^{2} + A_{1} D_{1}^{2}}{2} - a_{1} b_{1} = \frac{B_{1} D_{1}^{2}}{2} - a_{1} b_{1} . \end{matrix}

(1)

Itt a második tag egyenlő

N_{1}

-nek

t_{1}

területével, és az első tag is értelmezhető területként, egyenlő a

B_{1} D_{1}

mint átló fölé szerkesztett

B_{1} B_{1}^{*} D_{1} D_{1}^{*} = N_{1}^{*}

négyzet

t_{1}^{*}

területével. Eszerint

B_{1}^{*}

D_{1}^{*}

N_{1}

köré írt körben a

B_{1} D_{1}

-re merőleges átmérő végpontjai; válasszuk a jelölést úgy, hogy

A_{1} B_{1}^{*} < A_{1} D_{1}^{*}

legyen.
Ha mármost

α = B A D ∢ = B_{1} O A_{1} ∢ = 30^{\circ}

, akkor

O A_{1} B_{1}^{*}

egyenlő oldalú háromszög, ezért

B_{1}^{*}

2

-szer akkora távolságra van

O B_{1}

-től, mint

A_{1}

, tehát

N_{1}^{*}

területe

2

-szer akkora, mint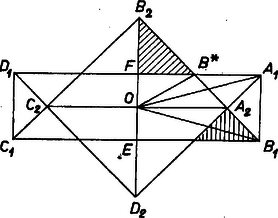

N_{1}

-é,

t_{1}^{*} = 2 t_{1}

, és (1)-ből

\begin{matrix} t_{2} = 2 t_{1} - t_{1} = t_{1} . \end{matrix}

Ezt kellett bizonyítanunk.

Gáspár András (Budapest, Vasútgépészeti techn. III. o. t.)

2. ábra

Megjegyzések. 1. Más úton bizonyítjuk, hogy ha egy téglalap átlóinak szöge

30^{\circ}

, akkor területe egyenlő a szögfelezői által határolt négyzet területével. Tükrözzük az

O A_{2}

egyenest

O A_{1}

-re mint tengelyre, és messe a kép

A_{1} D_{1}

-et

B^{*}

-ban (2. ábra). Így

A_{1} O B^{*} ∢ = A_{1} O A_{2} ∢ = O A_{1} B^{*} ∢

és

A_{2} O B^{*} ∢ = 2 \cdot A_{2} O A_{1} ∢ = B_{1} O A_{1} ∢ = 30^{\circ} = O B^{*} F ∢

, tehát egyrészt

O A_{1} B^{*}

egyenlő szárú háromszög, másrészt

O B^{*} F

fele egy egyenlő oldalú háromszögnek. Ezért

A_{1} B^{*} = O B^{*} = 2 \cdot F O = F E = A_{1} B_{1}

s mivel még

B_{1} A_{1} B^{*} ∢ = 90^{\circ}

, azért

B^{*}

rajta van a

B_{1} B_{2}

szögfelezőn. Vegyük egységnek

O F

-et, így

F B^{*} = \sqrt[]{3}

A_{1} B^{*} = 2

és

t_{1} = A_{1} B_{1} \cdot A_{1} D_{1} = 2 (4 + 2 \sqrt[]{3})

, másrészt

A_{2}

felezi

B_{1} B^{*}

-ot, ezért

O A_{2} = F B^{*} + B^{*} A_{1} / 2 = \sqrt[]{3} + 1

, és

t_{2} = 2 \cdot O A_{2}^{2} = 2 (4 + 2 \sqrt[]{3}) = t_{1}

, qu. e. d.
Ezek után az

N_{1}

és

N_{2}

területének egyenlősége abból is adódik, hogy a közös részükből kinyúló rész

N_{1}

-ben

6

N_{2}

-ben

4

egybevágó egyenlő szárú derékszögű háromszögre bontható, befogóik hossza

\sqrt[]{2}

, ill.

\sqrt[]{3}

, területeik aránya

2 : 3

, azaz

4 : 6

, így pedig a kinyúló területek egyenlők.
Tusnády Gábor

2. A versenyzők szinte kivétel nélkül trigonometriai számítással bizonyították az állítást; ezt vázoljuk.

N_{1}

területe

4

-szer akkora, mint az

O A_{1} B_{1}

háromszögé, oldalai pedig

α / 2

-vel fejezhetők ki:

\begin{matrix} t_{1} = 4 \cdot \frac{{(a - b)}^{2} sin α}{2 \cdot 4}, \\ b_{1} = A_{1} D_{1} = (a - b) cos \frac{α}{2}, a_{1} = A_{1} B_{1} = (a - b) sin \frac{α}{2}, \end{matrix}

így

N_{2}

átlói, majd területe, átalakítások után, majd a két terület aránya

\begin{matrix} A_{2} C_{2} = (a - b) \cdot | cos \frac{α}{2} - sin \frac{α}{2} |, t_{2} = \frac{1}{2} A_{2} C_{2}^{2} = \frac{{(a - b)}^{2} (1 - sin α)}{2}, \frac{t_{1}}{t_{2}} = \frac{sin α}{1 - sin α}, \end{matrix}

és ez

α = 30^{\circ}

esetén

1

.‐ Eszerint

α

kellő megválasztásával a

t_{1} / t_{2}

arány tetszés szerinti

k

értéket felvehet, ti. ha

\begin{matrix} sin α = \frac{k}{k + 1} . \end{matrix}

Deák Jenő (Budapest, Kölcsey F. g. IV. o. t.)