Kezdőlap


Feladat:	1445. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Antos P. , Argyelán J. , Bajna Zs. , Bárány Imre , Bod Judit , Cziffra A. , Deák J. , Domokos L. , Füvesi I. , Gáspár A. , Havas J. , Herényi I. , Iváncsy Sz. , Kádas S. , Kloknicer I. , Králik I. , Kuli Mária , Langer T. , Pintér J. , Sásdy B. , Szeredi P. , Szilágyi P. , Tiszai I. , Varga Gabriella
Füzet:	1967/február, 61 - 63. oldal		PDF \| MathML
Témakör(ök):	Körülírt kör, Kör egyenlete, Kör (és részhalmaza), mint mértani hely, Diszkusszió, Háromszögek szerkesztése, Parabola, mint mértani hely, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1966/február: 1445. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. rész. Az $M$ által leírt $k$ kör középpontja az $A B$ szakasz $O$ felezőpontja, sugara $O A$ , és $C$ az $A B$ -re merőleges átmérő egyik végpontja. Ezért elég $M$ -et pl. az $A C$ negyedíven végigfuttatni, hiszen ekkor $A B$ -re és $O C$ -re mint tengelyre, valamint $O$ -ra mint középpontra vett tükörképei ‐ rendre $M_{1}$ , $M_{2}$ , $M_{3}$ ‐ leírják $k$ további három negyedívét, és az $M_{j} A$ , $M_{j} B$ szakasz‐pár ( $j = 1$ , $2$ , $3$ ) megegyezik az $M A$ , $M B$ párral. Így pedig az $M_{j}$ helyzethez akkor és csak akkor szerkeszthető meg a kívánt háromszög, ha $M$ -hez megszerkeszthető.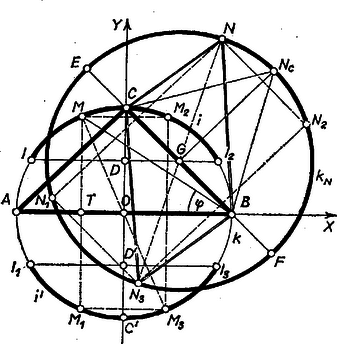

A választott negyedkörív pontjaira

M A ≦ C A = C B ≦ M B

, ezért a háromszög szerkeszthető voltának egyetlen feltétele:

\begin{matrix} M B < M A + B C, azaz M B - M A < B C . \end{matrix}

(1)

Itt a bal oldal pozitív vagy 0, ezért az egyenlőtlenség akkor és csak akkor teljesül, amikor a négyzetre emeléssel adódó egyenlőtlenség:

\begin{matrix} M B^{2} + M A^{2} - 2 M B \cdot M A < B C^{2} . \end{matrix}

(2)

Itt a kivonandó az

A B M

derékszögű háromszög területének 4-szerese, az első két tag összege pedig

A B^{2} = 2 B C^{2}

, ezért átrendezéssel és a területet az átfogóra vonatkozó

M T

magassággal kifejezve a feltétel

\begin{matrix} 2 \cdot M B \cdot M A = 2 \cdot A B \cdot M T > A B^{2} - B C^{2} = \frac{A B^{2}}{2}, \end{matrix}

(3)

amiből osztással (

A B > 0

alapján)

\begin{matrix} M T > \frac{A B}{4} = \frac{O C}{2} . \end{matrix}

(4)

Eszerint

k

-nak azokon az

I I_{2} = i

és

I_{1} I_{3} = i'

ívein levő pontjai felelnek meg

M

-ként, amelyeket az

A B

-re merőleges

C' C

átmérőt negyedelő

D

D'

pontokon át

A B

-vel párhuzamosan húzott szelők metszenek le. Az ívek végpontjai azonban már nem felelnek meg, mert ezekre (4)-ben egyenlőség áll fenn, és mivel azonos átalakításokat hajtottunk végre, visszamenve (1)-ben is egyenlőség áll, tehát elfajult háromszög jönne létre.

Bárány Imre (Budapest, Corvin Mátyás g. IV. o. t.)
dolgozata alapján

II. rész.

M

-nek egy az

i

-n levő helyzetéhez

N

részére két helyzet adódik,

N

és

N_{1}

, ezek a

B C

tengelyre nézve tükrös pontpárt alkotnak. Ugyanez a pontpár adódik ki

M

-nek fenti

M_{1}

tükörképéből is. Az

M

-nek fenti

M_{2}

és

M_{3}

tükörképeiből adódó

N_{2}

N_{3}

pontpár viszont ‐ az indexek kellő választásával ‐ nyilvánvalóan

N

és

N_{1}

tükörképe

B C

felező merőlegesére nézve. Így

N_{3}

egyszersmind

N

tükörképe a

B C

szakasz

G

felezőpontjára nézve, tehát a

B N C N_{3}

négyszög paralelogramma. Ebben az oldalak négyzetösszege

2 (N B^{2} + N C^{2}) = 2 (M B^{2} + M A^{2}) = 2 \cdot A B^{2} = 4 B C^{2}

állandó, úgyszintén a

B C

átló négyzete is állandó. Ezért ismert tétel szerint¹ az

N N_{3} = 2 N G

átló négyzete is állandó és

3 B C^{2}

-tel egyenlő. Ezért

N G

egyenlő

\sqrt[]{3} B C / 2

-vel, a

B C

oldal fölé szerkesztett

B C N_{c}

egyenlő oldalú háromszög

N_{c} G

magasságával (

N_{c}

akkor adódik, ha

M

C

-ben van), és így

N

mindig a

G

körül

G N_{c}

sugárral írt

k_{N}

körön van.
Megmutatjuk, hogy míg

M

befutja

i

-t,

N

k_{N}

kör minden pontjába eljut.

M

számára most már

i

és

i_{1}

fent kizárt végpontjai is figyelembe veendők, mert a követelmény nem írja elő, hogy

N

B

és

C

valódi háromszöget alkossanak.

M

-et

I

-ben, majd

I_{2}

-ben választva (1)-ben egyenlőség áll,

N

k_{N}

kör

B C

-n levő átmérőjének

E

, ill.

F

végpontjában adódik

(F B = E C < E B = F C)

. A körön tetszés szerint választott

N

-re nézve így

B N

hossza

B F

és

B E

hossza közé esik,

C N

-é pedig

C E

és

C F

közé, vagyis mindkettő

A I = B I_{2}

és

A I_{2} = B I

hossza közé, így az

N

-et előállító

M

pontot

k

-ból akár az

A

körüli

C N

sugarú, akár a

B

körüli

B N

sugarú körrel kimetszhetjük, hiszen e két kör

B N^{2} + C N^{2} = B M^{2} + A M^{2}

miatt ugyanabban a pontban metszi

k

-t.
Ezek szerint

N

pályája a

k_{N}

kör.

Megjegyzés. III‐IV. osztályos versenyzőink frissebb ismeretanyaguk, a trigonometria és a koordináta‐geometria eszközeivel vizsgálták a feladat II. részét, erre tekintettel vázolunk egy ilyen típusú megoldást is.
Legyen

M B A ∢ = φ (0^{\circ} ≦ φ ≦ 90^{\circ})

, és

A B = 1

; ekkor

M A = sin φ

M B = cos φ

B C = sin 45^{\circ}

, és (1) második alakjából

\begin{matrix} cos φ - sin φ = cos φ - cos (90^{\circ} - φ) = 2 sin 45^{\circ} sin (45^{\circ} - φ) < sin 45^{\circ}, \\ sin (45^{\circ} - φ) < 1 / 2, 45^{\circ} - φ < 30^{\circ}, φ > 15^{\circ}, M O A ∢ = 2 φ > 30^{\circ}, \end{matrix}

és így

M O > M C

, ill.

M O > M C'

.
Legyen továbbá egy derékszögű koordinátarendszer

X

-tengelye az

O B

Y

-tengelye az

O C

egyenes,

A

B

C

M

és

N

koordinátái rendre:

\begin{matrix} A (- 1 / 2, 0), B (1 / 2, 0), C (0, 1 / 2), M (x_{0}, \pm \sqrt[]{1 / 4 - x_{0}^{2}}), N (x, y) . \end{matrix}

Ezekkel

C N^{2} = A M^{2}

-ből

\begin{matrix} x^{2} + {(y - 1 / 2)}^{2} = {(x_{0} + 1 / 2)}^{2} + (1 / 4 - x_{0}^{2}) = x_{0} + 1 / 2, \end{matrix}

B N^{2} = B M^{2}

-ből

\begin{matrix} {(x - 1 / 2)}^{2} + y^{2} = {(x_{0} - 1 / 2)}^{2} + (1 / 4 - x_{0}^{2}) = - x_{0} + 1 / 2, \end{matrix}

és

x_{0}

kiküszöbölésével (összeadással)

\begin{matrix} 2 x^{2} - x + 2 y^{2} - y = 1 / 2, {(x - 1 / 4)}^{2} + {(y - 1 / 4)}^{2} = 3 / 8, \end{matrix}

vagyis

N

pályája a

G (1 / 4, 1 / 4)

pont ‐

B C

felezőpontja ‐ körüli

\sqrt[]{3} / 2 \sqrt[]{2} = \sqrt[]{3} \cdot B G

sugarú kör, vagy ennek része.
Most még bizonyítani kellene, hogy

N

ezt az egész körkerületet befutja, ami ezen a módon nehézkesebb volna.

¹Paralelogramma oldalainak négyzetösszege egyenlő az átlók négyzetösszegével. Lásd legutóbb 1040. gyakorlat, K. M. L. 33 (1966. nov.) 152. o.