Kezdőlap


Feladat:	1440. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Babai László , Bárány I. , Domokos László , Kádas S. , Szeredi P.
Füzet:	1967/március, 98 - 100. oldal		PDF \| MathML
Témakör(ök):	Vetítések, Féligszabályos testek, Sokszögek szerkesztése, Szabályos sokszögek geometriája, Szabályos sokszögek szerkesztése, Feladat
Hivatkozás(ok):	Feladatok: 1966/január: 1440. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.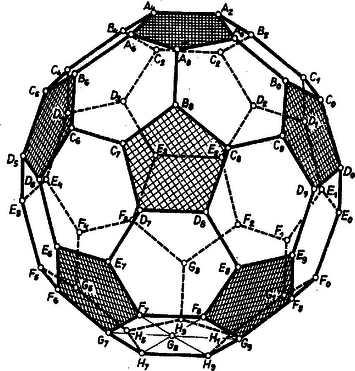

1. ábra

I. Az állításokat az

F_{7} F_{8}

élre bizonyítjuk. A lapok szabályos és egybevágó voltából és a poliéder felépítésének elvéből következik, hogy bizonyításunk bármely élre érvényes.
A lapok szabályos voltából következik, hogy

F_{7} F_{8}

-cal párhuzamos a benne csatlakozó két hatszöglapnak vele szemben levő

D_{7} D_{8}

, ill.

H_{7} H_{9}

éle, valamint az első hatszöglaphoz

D_{7} D_{8}

mentén csatlakozó ötszöglap

C_{7} C_{8}

átlója. Ugyanígy adódik, hogy

A_{6} A_{0} ∥ A_{4} A_{2} ∥ C_{3} C_{2} ∥ E_{3} E_{2}

. Másrészt

C_{7} C_{8} ∥ A_{6} A_{0}

, mert

A_{6} C_{7} # A_{0} C_{8}

, hiszen hatszöglapok leghosszabb átlói, és párhuzamosak az

A_{8} B_{8}

éllel. Ezek szerint a poliéder következő

6

éle párhuzamos:

\begin{matrix} H_{7} H_{9}, F_{7} F_{8}, D_{7} D_{8}, A_{4} A_{2}, C_{3} C_{2}, E_{3} E_{2} . \end{matrix}

(1)

Nem volt lényeges, hogy két egynemű lap közös éléből indultunk ki; hiszen a

6

párhuzamos él közül

4

-ben

1

hatszöglap és

1

ötszöglap csatlakozik egymáshoz.
Az

A_{8} B_{8}

él benne van a

C_{7} C_{8}

lapbeli átló

S

felező merőleges síkjában, mert végpontjai egyenlő távol vannak

C_{7}

-től és

C_{8}

-tól, ugyanis

A_{8} C_{7}

és

A_{8} C_{8}

a hatszöglap rövidebb átlói. Ezért

A_{8} B_{8}

merőleges

C_{7} C_{8}

-ra és a vele párhuzamos

F_{7} F_{8}

-ra. Ugyanígy adódik, hogy

E_{9} F_{9} ⊥ F_{7} F_{8}

. Mármost

A_{8} B_{8}

-hoz is,

E_{9} F_{9}

-höz is a fentiekhez hasonlóan felsorolható további

5

‐

5

, velük párhuzamos éle a poliédernek és a két felsorolásban egy él sem ismétlődik; ezekben megtaláltuk a poliédernek

F_{7} F_{8}

-ra merőlegesen álló

12

élét:

\begin{matrix} B_{0} C_{9}, & A_{8} B_{8}, & B_{6} C_{6}, & F_{4} G_{5}, & G_{3} H_{3}, & F_{1} G_{1}; & (2) \\ C_{1} D_{1}, & D_{0} E_{0}, & E_{9} F_{9}, & E_{6} F_{6}, & D_{5} E_{5}, & C_{4} D_{4} . \end{matrix}

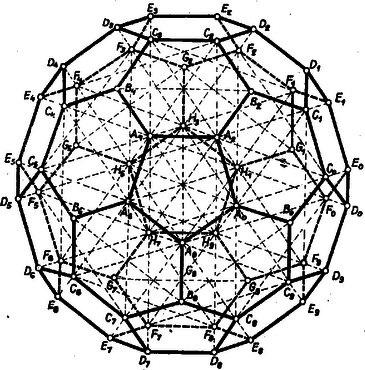2. ábra

II. Tekintsük a rajzsíkon adottnak az 1. ábra

H_{1} H_{3} H_{5} H_{7} H_{9} = H

ötszöglapját (2. ábra). A vetületnek

H

síkján leendő megszerkesztésében a fentieken túl felhasználjuk a következőket.

S

az (1) élek mindegyikét merőlegesen felezi ‐ úgyszintén a következő, velük párhuzamos lapbeli átlókat is:

\begin{matrix} C_{7} G_{9}, & E_{7} E_{8}, & B_{4} B_{2}, & D_{3} D_{2}; & (3) \\ C_{7} C_{8}, & A_{6} A_{0}, & F_{3} F_{2}, & H_{5} H_{1}, & (4) \end{matrix}

hiszen szabályos sokszög bármely oldalának, átlójának felező merőleges egyenese a sokszögnek szimmetriatengelye, és felező merőleges síkja a sokszögnek szimmetriasíkja. Így

S

merőleges

H

síkjára, és átmegy a

H_{3} G_{3}

élen.
Eszerint

S

-nek

H

síkján levő vetülete a

H_{7} H_{9}

oldal felező merőlegese, vagyis átmegy

H_{3}

-on; az (1) élek vetülete a rajzsíkon

H_{7} H_{9}

-nek önmagára merőleges eltolásával áll elő, az előforduló,

H_{7}

-től és

H_{9}

-től különböző

10

csúcs vetülete rajta van a

H_{7} H_{9}

-re a végpontjaiban állított merőlegesek egyikén. Ugyanígy a (4) átlók végpontjaiként szereplő

6

új csúcs vetülete rajta van a

H_{5}

-ön,

H_{1}

-en át

H_{7} H_{9}

-re állított merőlegesek egyikén. Végül

A_{8}

B_{8}

G_{3}

vetülete a

H_{3}

-on át

H_{7} H_{9}

állított merőlegesen van rajta.
A mondott

5

merőleges a derékszögű háromszögvonalzó szokásos megtámasztásával, majd

90^{\circ}

-os elfordításával megrajzolható. Ezt

H

további oldalaival megismételve könnyű belátni, hogy a metszéspontok közül kiválasztható a következő

25

csúcs vetülete:

\begin{matrix} F_{0}, F_{1},1 ..., F_{9}; C_{0}, C_{1}, ..., C_{9}; A_{0}, A_{2}, ..., A_{8}, \end{matrix}

pl.

F_{7}

H_{7}

-en át

H_{7} H_{9}

-re és

H_{9}

-en át

H_{1} H_{3}

-ra állított merőlegesek metszéspontja, mert

F_{7} F_{8} # H_{7} H_{9}

és (4)-höz hasonlóan

F_{7} F_{6} # H_{9} H_{5} ∥ H_{1} H_{3}

;

C_{2}

H_{5}

-ön át

H_{1} H_{3}

-ra és

H_{9}

-en át

H_{7} H_{9}

-re állított merőlegesek,

A_{0}

pedig a

H_{1}

-en át

H_{7} H_{9}

-re és

H_{9}

-en át

H_{1} H_{3}

-ra állított merőlegesek metszéspontja, mert

A_{0} A_{4} # H_{5} H_{9} ∥ H_{1} H_{3}

.
A megrajzolt merőlegesek további metszéspontjai között szerepel

10

hatszög lap középpontjának vetülete, mint a hatszög két párhuzamos oldalával meghatározott téglalap átlóinak metszéspontja. Ezen át mindig megrajzolható a hatszög hátra levő leghosszabb átlójának egyenese, és ez a korábbi egyenesekből kimetszi a

\begin{matrix} G_{1}, G_{3},1 ..., G_{9}; B_{0}, B_{2}, ..., B_{8} \end{matrix}

csúcsok vetületét. Pl.

H_{7} F_{8}

és

H_{9} F_{7}

metszéspontján át (az ábrákon

G_{8}

)

H_{7} H_{9}

-cel párhuzamost húzva kapjuk a

G_{7} G_{9}

átló végpontjait, a vetület

H_{7}

-en, ill.

H_{9}

-en átmenő tengelyén. (Elég

6

-ot megrajzolni az ilyen átlók közül.)
A hátra levő

D_{i}

E_{i}

csúcsok

(i = 0, 1, ... 9)

vetületei közül

D_{1}

-ét.

E_{9}

-ét,

E_{6}

-t és

D_{4}

-ét (2) második sora alapján kapjuk abból, hogy ezeknek az éleknek a képe merőleges

H_{7} H_{9}

-re, mivel maguk az élek párhuzamosak

S

-sel és ‐ mint majd belátjuk ‐ nem merőlegesek

H

síkjára. Felhasználjuk

C_{1}

F_{9}

F_{6}

és

C_{4}

már meglevő képét. Pl. a

C_{1}

képén át

H_{7} H_{9}

-re állított merőleges a

H_{1}

-en átmenő,

H_{1} H_{3}

-ra merőleges (már megrajzolt) egyenesből metszi ki

D_{1}

képét (egyszersmind ‐ mint a szimmetriából könnyen látható ‐

E_{9}

-et is, a

H_{3}

-on át

H_{3} H_{5}

-re állított merőlegesből). Innen látjuk, hogy

C_{1} D_{1}

képe nem pont, hiszen

C_{1}

D_{1}

képe különböző, de a

H_{1} H_{3}

-ra merőleges egyenesen van rajta. ‐ A további

D

és

E

csúcsok vetületét hasonlóan megszerkesztve, a poliéder vetületének előállítását befejeztük (együttvéve

10

egyenes).
Valóban, csak párhuzamos és merőleges egyeneseket kellett rajzolnunk

H

csúcsain, valamint a közben adódott pontokon át (szám szerint

41

-et). A csúcsok vetületeinek összekötésével kapjuk az élek vetületét (a

90

élből

30

-nak a képe a szerkesztő egyeneseknek egy-egy szakasza).

Domokos László (Tatabánya, Árpád Gimn., IV. o. t.)
Babai László (Budapest, Fazekas M. Gyak. Gimn., II. o. t.)

Megjegyzés. A sportéletre való hivatkozással lényegében elfogadtuk a szóban forgó poliéder létezését. Ezt azonban a vetület megrajzolása sem bizonyítja. Mindjárt az is kételkedést támaszthat, hogy

1

ötszöglapnak és

2

hatszög lapnak egy csúcsba összeillesztése a lapok közti szögeket ‐ vagy ami ezek számítását lehetővé teszi, egy csúcs távolságát a vele szomszédos csúcsba befutó harmadik lap síkjától ‐ az 1454. feladatban^{$^{*}$}) látottakhoz hasonlóan egyértelműen meghatározza.
Önálló bizonyítás helyett gondoljuk át, hogy poliéderünk előállítható az 1472. feladatban^{$^{*}$} vizsgált (és bebizonyítottan létező) szabályos ikozaéderből úgy, hogy rendre vesszük az egy csúcsából kiinduló

5

él mindegyikén a hozzá közelebbi harmadoló pontot és az ezekkel meghatározott sík egyik oldalán előálló szabályos ötoldalú gúlát lemetsszük az ikozaéderből.

^{$^{*}$}Lásd ezen számban 102. o.

^{$^{*}$}K. M. L. 34 (1967. jan.) 19. o.