Kezdőlap


Feladat:	1437. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Babai L. , Bárány I. , Baróthy B. , Bod Judit , Bottyán I. , Domokos L. , Gács P. , Gáspár A. , Gy. Molnár Csaba , Herényi I. , Joó I. , Kádas S. , Kafka P. , Karsai I. , Kiss A. , Kloknicer I. , Korchmáros G. , Lakatos L. , Langer T. , Lévai F. , Medgyesy K. , Medveczky M. , Pintér J. , Recski A. , Sebő I. , Sólymos L. , Sugár L. , Szeidl L. , Szentgáli Á. , Szeredi P. , Szilágyi P. , Tihanyi László , Tolnay-Knefély T. , Varga Gabriella , Verdes S.
Füzet:	1966/december, 206 - 208. oldal		PDF \| MathML
Témakör(ök):	Ceva-tétel, Egyenesek egyenlete, Terület, felszín, Szinusztétel alkalmazása, Síkgeometriai számítások trigonometriával, Feladat
Hivatkozás(ok):	Feladatok: 1966/január: 1437. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A szerkesztés szerint a $G H J = T'$ háromszög nagyon kicsi az $A B C = T$ háromszöghöz képest (a segédábra a $G H J$ háromszöget lineárisan 100-szoros nagyításban mutatja).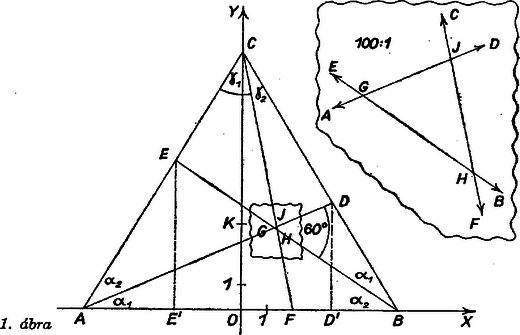

1. ábra

B D = C E

és a

T

háromszög szabályos volta miatt az

A B D

és

B C E

háromszögek azonos körüljárásúan egybevágók, és

T

-nek

K

középpontja körüli

120^{\circ}

-os forgatásával egymással fedésbe hozhatók. Ezért

B E

A D

-nek elforgatottja,

D G E ∢ = A G B ∢ = 120^{\circ}

, és mivel

C

és

F

ezekben a szögtartományokban vannak,

H

és

J

vagy a

B G D

vagy az

A G E

szög szárain vannak, ezért mindenesetre

H G J ∢ = 60^{\circ} = A B C ∢

. Így a keresett arány, a területeket ugyanúgy jelölve, mint magukat a háromszögeket:

\begin{matrix} T' : T = \frac{G H \cdot G J sin 60^{\circ}}{2} : \frac{A B \cdot A C sin 60^{\circ}}{2} = G H \cdot G J : 144, \end{matrix}

és

G H

-t megadja a

B G

és

B H

G J

-t pedig az

A J

és

A G

szakaszok különbségének abszolút értéke.
E szakaszok az

A B G

B C H

, ill.

C A J

háromszögben oldalak, kifejezhetők

T

oldalával és a csúcsoknál keletkezett (az 1. ábra szerint jelölendő) szögekkel a színusz-tétel alapján:

\begin{matrix} B G = \frac{A B sin α_{1}}{sin A G B ∢} = \frac{24 sin α_{1}}{\sqrt[]{3}}, B H = \frac{B C sin γ_{2}}{sin B H C ∢} = \frac{12 sin γ_{2}}{sin (α_{1} + γ_{2})}, \\ A G = \frac{A B sin α_{2}}{sin A G B ∢} = \frac{24 sin α_{2}}{\sqrt[]{3}}, A J = \frac{C A sin γ_{1}}{sin C J A ∢} = \frac{12 sin γ_{1}}{sin (α_{2} + γ_{1})} . \end{matrix}

Ezek céljára az

A B D

B C F

A C F

A C D

háromszögből a koszinusz-tétel, a színusz-tétel és az addíció tétel alapján

A D^{2} = A B^{2} + B D^{2} - 2 A B \cdot B D cos 60^{\circ} = 109, C F^{2} = 112;

\begin{matrix} cos α_{1} = \frac{19}{2 \sqrt[]{109}}, cos α_{2} = \frac{17}{2 \sqrt[]{109}}, cos γ_{1} = \frac{2}{\sqrt[]{7}}, cos γ_{2} = \frac{5}{2 \sqrt[]{7}}; \\ sin α_{1} = \frac{5 \sqrt[]{3}}{2 \sqrt[]{109}}, sin α_{2} = \frac{7 \sqrt[]{3}}{2 \sqrt[]{109}}, sin γ_{1} = \frac{\sqrt[]{3}}{\sqrt[]{7}}, sin γ_{2} = \frac{\sqrt[]{3}}{2 \sqrt[]{7}}; \\ sin (α_{1} + γ_{2}) = \frac{11 \sqrt[]{3}}{\sqrt[]{7 \cdot 109}}, sin (α_{2} + γ_{1}) = \frac{31 \sqrt[]{3}}{2 \sqrt[]{7 \cdot 109}} . \end{matrix}

Így pedig a keresett szakaszok hossza, valamint a területek aránya

\begin{matrix} B G = \frac{60}{\sqrt[]{109}}, B H = \frac{6 \sqrt[]{109}}{11}, G H = \frac{6}{11 \sqrt[]{109}} (\approx 0, 052), \\ A G = \frac{84}{\sqrt[]{109}}, A J = \frac{24 \sqrt[]{109}}{31}, G J = \frac{12}{31 \sqrt[]{109}} (\approx 0, 037), \\ \frac{T'}{T} = \frac{G H \cdot G J}{144} = \frac{1}{2 \cdot 11 \cdot 31 \cdot 109} = \frac{1}{74 338} . \end{matrix}

Gy. Molnár Csaba (Miskolc, Bláthy O. Villamosip. techn. III. o. t.)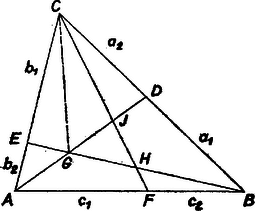

2. ábra

Megjegyzés. Tetszés szerinti

A B C

háromszögből kiindulva (2. ábra) az

A G B

és

A G C

háromszögek területeinek aránya egyenlő

A G

-re merőleges magasságaik arányával, ez pedig a

B D = a_{1}

és

C D = a_{2}

szakaszok arányával:

\begin{matrix} A G B : A G C = a_{1} : a_{2} . \end{matrix}

Ugyanígy

B G A : B G C = b_{2} : b_{1}

, és

A B C = A B G + B G C + C A G

miatt, továbbá hasonlóan

\begin{matrix} A B C = A B G (1 + \frac{b_{1}}{b_{2}} + \frac{a_{2}}{a_{1}}), A B G = \frac{a_{1} b_{2} \cdot A B C}{a_{1} b_{1} + a_{1} b_{2} + a_{2} b_{2}} = k_{1} \cdot A B C; \\ B C H = \frac{b_{1} c_{2} \cdot A B C}{b_{1} c_{1} + b_{1} c_{2} + b_{2} c_{2}} = k_{2} \cdot A B C, C A J = \frac{c_{1} a_{2} \cdot A B C}{c_{1} a_{1} + c_{1} a_{2} + c_{2} a_{2}} = k_{3} \cdot A B C . \end{matrix}

Ezekből

G H J = A B C - A B G - B C H - C A J

alapján, kellő rendezés után

\begin{matrix} \frac{G H J}{A B C} = 1 - k_{1} - k_{2} - k_{3} = \\ = \frac{{(a_{1} b_{1} c_{1} - a_{2} b_{2} c_{2})}^{2}}{(a_{1} b_{1} + a_{1} b_{2} + a_{2} b_{2}) (b_{1} c_{1} + b_{1} c_{2} + b_{2} c_{2}) (c_{1} a_{1} + c_{1} a_{2} + c_{2} a_{2})} . \end{matrix}

Innen

a_{1} = b_{1} = 5

a_{2} = b_{2} = 7

c_{1} = 8

c_{2} = 4

esetére a fenti arányértéket kapjuk.
Amennyiben az

A D

B E

C F

egyenesek egy

P

ponton mennek át,

G

H

J

egybeesnek, a velük meghatározott háromszög területe 0, és így

a_{1} b_{1} c_{1} = a_{2} b_{2} c_{2}

. Ez Ceva tétele.
(Tusnády Gábor)

Kevesebb számolással érünk célt a koordináta-geometria eljárásával.

II. megoldás. Helyezzünk az adott háromszögre derékszögű koordinátarendszert,

X

-tengelynek az

A B

egyenest,

Y

-tengelynek a

C

-n átmenő magasság egyenesét választva. Így a csúcsok koordinátái

A (- 6; 0)

B (6; 0)

C (0; 6 \sqrt[]{3})

, a kijelölt pontoké pedig

D (3, 5; 2, 5 \sqrt[]{3})

E (- 2, 5; 3, 5 \sqrt[]{3})

F (2; 0)

, ugyanis az első kettőnek az

X

-re való vetületét

D'

-vel,

E'

-vel jelölve

B D D'

és

A E E'

egy szabályos háromszög fele, és

A E = 7

. Ezekből a megrajzolt egyenesek egyenlete, majd a kérdéses metszéspontok koordinátái:

\begin{matrix} A D : 19 y = 5 \sqrt[]{3} (x + 6), B E : - 17 y = 7 \sqrt[]{3} (x - 6), \\ C F : y = - 3 \sqrt[]{3} (x - 2); \\ G (\frac{144}{109}, \frac{210 \sqrt[]{3}}{109}), H (\frac{15}{11}, \frac{21 \sqrt[]{3}}{11}), J (\frac{42}{31}, \frac{60 \sqrt[]{3}}{31}) . \end{matrix}

A csúcsainak koordinátáival meghatározott háromszög területképletét¹ alkalmazva a

G H J

háromszögre

\begin{matrix} t = [x_{1} (y_{2} - y_{3}) + x_{2} (y_{3} - y_{1}) + x_{3} (y_{1} - y_{2})] / 2 = \frac{18 \sqrt[]{3}}{11 \cdot 31 \cdot 109}, \end{matrix}

másrészt az

A B C

háromszög területe

A B \cdot O C / 2 = 36 \sqrt[]{3}

. Ennélfogva a keresett arányszám

1 / (2 \cdot 11 \cdot 31 \cdot 109) = 1 / 74 338.

Tihanyi László (Makó, József A. g. III. o. t.)

¹Lásd Lóky B.: Négyjegyű függvény táblázatok, 19. kiadás, Tankönyvkiadó, Budapest, 1962, 23. o.