Kezdőlap


Feladat:	1436. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Babai László , Bán P. , Bárány L. , Berkes Z. , Bod Judit , Deák Jenő , Domokos László , Gáspár András , Havas J. , Herényi I. , Kádas S. , Karsai I. , Kiss Á. , Kloknicer I. , Külvári I. , Lakatos L. , Recski A. , Solymos A. , Solymosi András , Szeidl L. , Szentgáli Á. , Szeredi P. , Szilágyi P. , Tihanyi L. , Tolnay-Knefély T. , Varga Gabriella
Füzet:	1966/december, 203 - 205. oldal		PDF \| MathML
Témakör(ök):	Numerikus és grafikus módszerek, Síkgeometriai számítások trigonometriával, Feladat
Hivatkozás(ok):	Feladatok: 1966/január: 1436. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Válasszuk hosszúságegységnek az $O A = O B$ sugarat, és legyen az $A O C$ szög ívmértéke $x$ ; $C$ korlátozása miatt $0 < x < π / 2$ . Így $O D B ∢ = x$ , és $B D = cotg x$ (1. ábra), a körcikk és a háromszög területe $x / 2$ , ill. ( $cotg x) / 2$ , ezért az

\begin{matrix} x / cotg x = k, másképpen x / k = cotg x \end{matrix}

egyenletet kell megoldanunk

k = 2

, 1 és 1/2 eseteire.

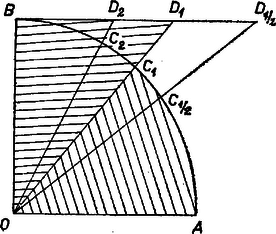1. ábra

Ilyen egyenletek pontos megoldására nem ismeretes eljárás, de a megoldás közelítően megkapható, pontosságát a rendelkezésre álló cotg-táblázat pontossága szabja meg. Az előírt pontosság

57, 3^{\circ} / 1000

, azaz elég

x

-et

0, 05^{\circ}

-nyira meghatározni. ‐ Első közelítő értéket mindhárom esetben az egyenlet két oldalának grafikus ábrázolása útján keresünk, a metszéspont abszcisszáját leolvasva. A 2. ábra eredetijén az egység 10 cm (a nyomtatásban kicsinyítve van felére), az előírt 0,001 pontosságnak 0,1 mm felel meg, így a leolvasás pontossága nem lesz elegendő. Ezért a kapott helyen kiszámítjuk a két oldal különbségét (közelítésünk hibáját), ebből és a grafikonok menetéből javítjuk az első közelítő értéket, vagyis következtetünk arra, hogy melyik irányban és kb. mekkora távolságban van a (valódi) metszéspont. Az így adódó újabb közelítő értékkel ismételjük eljárásunkat, míg a kellő pontosságot elérjük.

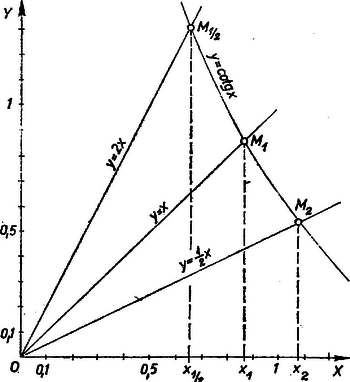2. ábra

k = 1

esetén az

y = x

egyenes és az

y = cotg x

görbe

M_{1}

metszéspontjának

x_{1}

abszcisszájára mm pontossággal

x_{1}' \approx 0, 86

-ot olvasunk le. Fokra átszámítva

x'_{1} = 180^{\circ} \cdot 0, 86 / π = 49, 275^{\circ}

, így

cotg x_{1}' = 0, 8609

, tehát ezen a helyen a görbe ordinátája nagyobb az egyenes ordinátájánál. Mivel az egyenes (balról jobbra haladva) emelkedik, és a görbe süllyed, azért metszéspontjuk nagyobb abszcisszán lesz:

x_{1} > 0, 86

. Szemlélet szerint a süllyedés kissé meredekebb, mint az emelkedés, így a két ordináta közti 0,0009 különbség a metszéspontig úgy oszlik el, hogy kisebb része jut az egyenes emelkedésére, mint a görbe süllyedésére, vagyis azt sejtjük, hogy

M_{1}

ordinátája kisebb a két ordináta számtani közepénél, 0,86045-nél. Valóban, az

x''_{1} = 0, 8604 = 49, 30^{\circ}

második közelítő érték esetében már

cotg x''_{1} = 0, 8601 < x''_{1}

, ezért

x_{1} < 0, 8604

, tehát

10^{3}

-ra kerekítve

x_{1}

= 0,860.

k = 2

esetében az

y = x / 2

egyenes és a görbe

M_{2}

metszéspontjára közelítőleg

x'_{2} = 1, 08 = 61, 88^{\circ}

olvasható le. Ebből

cotg x'_{2} = 0, 5344 < 0, 54 = x'_{2} / 2

, ezen az abszcisszán a görbe már alatta van az egyenesnek, ezért

x_{2} < 1, 08

. A görbe meredekebben süllyed, mint ahogyan az egyenes emelkedik, ebből azt sejtjük, hogy

M_{2}

ordinátája nagyobb 0,5344 és 0,5400 számtani közepénél (0,5372-nél), próbálkozzunk ezért 0,538-del, ami az egyenesen az

x''_{2}

=1,076-hez, azaz

61, 59^{\circ}

-hoz tartozó ordináta. Itt

cotg x''_{2} = 0, 5396 > x''_{2} / 2

; tehát

x''_{2} < x_{2} < x'_{2}

. Az újabb eltérés

0, 5396 - 0, 538 = 0, 0016

, harmadát sem teszi ki az előbbi

0, 5344 - 0, 54 = - 0, 0056

abszolút értékének ezért harmadik próbálkozásként

x'_{2}

és

x''_{2}

között az utóbbihoz közelebbi

x'''_{2} = 1, 077

-et, azaz

61, 70^{\circ}

-ot vesszük. Itt

cotg x'''_{2} = 0,5384 \approx x'''_{2} / 2

, különbségük

- 0, 0002

, tehát

10^{- 3}

-ra kerekítve x

_{2} = 1, 077

.
Végül

k = 1 / 2

esetében a görbe és az

y = 2 x

egyenes

M_{1 / 2}

metszéspontjára közelítőleg

x'_{1 / 2} \approx 0, 65 = 37, 24^{\circ}, cotg x' 1 / 2 = 1, 315 > 2 x'_{1 / 2}

, így

x_{1 / 2} > x'_{1 / 2}

, és

cotg x'_{1 / 2} - 2 x'_{1 / 2} = 0, 015

. A görbe valamivel meredekebben süllyed, mint ahogyan

y = 2 x

emelkedik, várható, hogy

M_{1 / 2}

ordinátája

1, 30

és

1, 315

közepe, azaz

1, 3075

alatt lesz, próbálkozzunk

y = 2 x''_{1 / 2}

1, 306

-del, amiből

x''_{1 / 2} = 0, 653 = 37, 41^{\circ}, cotg x''_{1 / 2} = 1, 307, cotg x''_{1 / 2} - 2 x''_{1 / 2} = + 0, 001

. Viszont

x'''_{1 / 2} = 0, 6535

esetén már

cotg x'''_{1 / 2} - 2 x'''_{1 / 2} = - 0, 001

, ezért a kívánt pontossággal

x_{1 / 2} = 0, 653

.
Solymosi András (Budapest, Petőfi S. g. IV. o. t.)

Megjegyzés. Az első közelítő értékek javítása céljára a szemléletre támaszkodva végzett meggondolásnál valamivel pontosabbnak látszik a következő. Egyenletünk átírható

\begin{matrix} x tg x - k = 0 \end{matrix}

alakba. Legyen a gyök egy jó közelítő értéke

x_{0}

, vagyis

x_{0} \cdot tg x_{0} - k \neq 0

, de a bal oldal

| x_{0} \cdot tg x_{0} - k | = | d_{0} |

abszolút értéke kicsi a különbség tagjainak abszolút értékéhez képest. Erre támaszkodva közelítő értéket keresünk az

x

gyök és az

x_{0}

közelítő érték

h

különbségére abból, hogy várhatóan ez is kicsi érték

x_{0}

-hoz képest.

x - x_{0} = h

-ból

x = x_{0} + h

, ez kielégíti az egyenletet, vagyis

\begin{matrix} (x_{0} + h) tg (x_{0} + h) - k = (x_{0} + h) \cdot \frac{tg x_{0} + tg h}{1 - tg x_{0} \cdot tg h} - k = 0. \end{matrix}

(1)

A törtet eltávolítva az egyenlet így rendezhető át:

\begin{matrix} (x_{0} tg x_{0} - k) + h (tg x_{0} + x_{0} + k tg x_{0}) + \end{matrix}

(2)

\begin{matrix} + (tg h - h) (x_{0} + k tg x_{0}) + h \cdot tg h = 0. \end{matrix}

A bal oldal utolsó két tagját az előbbiek mellett elhanyagolhatjuk. Ismeretes ugyanis, hogy a

0^{\circ} - 5^{\circ}

közti szögek tangense közelítőleg egyenlő ívmértékükkel, ezért a 3. tagbeli

(tg h - h)

tényező kicsi a 2. tagbeli

h

-hoz képest (és e két tag másik tényezői közül is az előbbi a nagyobb), a 4. tagnak pedig várhatóan mindkét tényezője kicsi. Mivel az első zárójelben

d_{0}

áll, azért (2) meghagyott tagjaiból közelítőleg

\begin{matrix} h \approx - \frac{d_{0}}{x_{0} + (k + 1) tg x_{0}} . \end{matrix}

Pl. a fenti

k

=0,5 és

x_{0} = 0, 65 = 37, 24^{\circ}

esetében tg

x_{0} = 0, 7601, d_{0} \approx 0, 4941 - 0, 5 = - 0, 0059

(kisebb, mint a különbség tagjainak

2 %

-a), ezekből

h \approx

0,0033 és

x'_{1 / 2} + h

=0,6533, kerekítve

0, 653

. (Így

h = 0, 19^{\circ}, tg h = 0, 0033

és

h \cdot tg h \approx 1,1 \cdot 10^{- 5}

, valóban alatta van annak a

10^{- 4}

hibának, amit a táblázat használatával elkövethetünk.)^{$^{*}$}

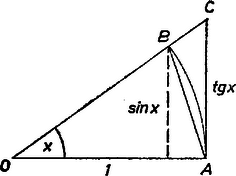3. ábra

^{$^{*}$}Az iskolai függvénytáblázat szerint

sin x

és

tg x

értéke

10^{- 4}

-re kerekítve még

x = 2, 6^{\circ}

-nál egyenlő. Másrészt a szög ívmértéke a 3. ábra szerint ezek közé esik

(0 < x < π / 2

esetén)

sin x < x < tg x

, mert

sin x

-et az

O A B

háromszög,

x

-et az

O A B

körcikk,

tg x

-et az

O A C

háromszög 2-szeres területe szemlélteti.