Kezdőlap


Feladat:	1431. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Antos P. , Babai L. , Bárány I. , Domokos L. , Gegesy F. , Kádas S. , Kiss Á. , Lévai F. , Papp Z. , Pintz J. , Szeredi P. , Szilágyi P. , Tolnay-Knefély T.
Füzet:	1967/február, 59 - 60. oldal		PDF \| MathML
Témakör(ök):	Egyenletek grafikus megoldása, Hossz, kerület, Alakzatok mértéke, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1965/december: 1431. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

¹
Induljunk ki a versenyfeladatnak az idézett helyen közölt II. megoldásából, a híd két kapuzatának a megfigyelő álláspontján áthaladó $11, 4^{\circ}$ , ill. $4, 7^{\circ}$ nyílásszögű látókörívéből. A látószögek megengedett értékingadozása miatt minden egyes az (1)-nek eleget tevő értékhez szóba jön egy körív. Ez kissé eltér a felhasznált ívtől, mert a szöget pl. növelve, a körív középpontja közeledik a kapuzathoz, és a sugár csökken. Elég venni a legnagyobb és a legkisebb látószögértékhez tartozó ívet, ezek egy kifli alakú, körgyűrű‐szerű, két csúcsú idomot határolnak (1. ábra), a csúcsok a kapuzatot jelképező szakasz végpontjai, minden közbe eső szögértékhez tartozó látószög‐körív az idom belsejében halad és a két csúcsban végződik.

Az eredeti megoldás két körívének

P

közös pontja, a megfigyelő álláspontja helyére a két kifli‐idom közös pontjai lépnek, mert minden közös ponton áthalad egy

α

-ív és egy

β

-ív. A közös pontok várhatóan ugyancsak egy idomot töltenek ki, melynek pontjai különböző magasságban lesznek az

O_{1} O_{2}

szint fölött, ezért kézenfekvő a versenyfeladat kérdését így módosítani: mekkora a megfigyelő legnagyobb és legkisebb lehetséges magassága a kapuzatok talppontján átmenő vízszintes sík fölött?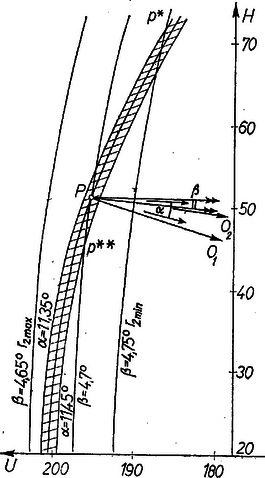

2. ábra

Tájékozódás céljára készítsünk mérethű ábrát a II. megoldás

P O_{1} O_{2}

háromszögéről a

t_{1} = 99, 2

r_{1} = 101, 2

t_{2} = 243, 2

r_{2} = 244, 1

m részeredmények, valamint a

d = 290

m adat alapján (2. ábra²), majd számítsuk ki a kifli‐idomokat határoló körívek középpontjának a kapuzathoz viszonyított helyzetét és sugarát, és rajzoljuk föl ezeket az íveket is.

\begin{matrix} \begin{matrix} α_{min} = 11, 35^{\circ} -ból & t_{1 max} = 99, 7 m, & r_{1 max} = 101, 7 m; \\ α_{max} = 11, 45^{\circ} -ból & t_{1 min} = 98, 7 m, & r_{1 min} = 100, 7 m; \\ β_{min} = 4, 65^{\circ} ból & t_{2 max} = 245, 9 m, & r_{2 max} = 246, 8 m; \\ β_{max} = 4, 75^{\circ} -ból & t_{2 min} = 240, 6 m, & r_{2 min} = 241, 5 m . \end{matrix} \end{matrix}

(Annak nincs jelentősége, hogy

β

nem veheti föl e két értéket, mert ennek ellenére tetszés szerint közel állhat hozzájuk; egyébként a hosszúságok maximális adatait fölfelé, a minimálisokat lefelé kerekítettük.)
A kiegészített ábra szerint a kifli‐idomok közös részének legmagasabb pontjára,

P^{*}

-ra nézve,

h_{max} \approx 73

méter, és (a szimmetriát tekintetbe véve)

h = - 73

m és

h = 73

m között minden magasságban van közös pont. Valóban, a köríveknek az

O_{1} O_{2}

egyenesen levő, a közelebbi kapuzattól legtávolabbi pontjának távolsága

u = t_{1} + r_{1}

u = t_{2} + r_{2} - d

, a fenti adatokból

201, 4

m és

199, 4

m, ill.

202, 7

m és

192, 1

m, tehát az

α

-hoz tartozó kifli‐idom nem metszi a

β

-hoz tartozó idom külső határvonalát. A

P^{*}

pontra nézve a versenyfeladatbeli számításokat az

α_{min}

β_{max}

látószög‐párral megismételve mindkét megoldás eljárása szerint

h \approx 73

m adódik.

Megjegyzések. 1. Eredményünk azt mutatja, hogy a

β

meghatározásában megengedett bizonytalanság az egész eljárást használhatatlanná tenné. (Ámde

0, 05^{\circ} = 3'

sokkal nagyobb hiba a szokásos teodolitokkal elérhető

10 - 20''

, sőt

1''

alatti pontosságnál!)
Ábránkból azt is látjuk, hogy ha a

β = 4, 7^{\circ}

adatra azt tennők fel, hogy

0, 1^{\circ}

-ra lefelé kerekítéssel adódott, akkor már csak a

45 < h < 73

magasságértékek jöhetnének szóba az észlelő álláspontjára nézve, hiszen így a

β

-val adódó kifli‐idom külső határvonala

P^{* *}

-ban metszené az

α

-idom belső határvonalát.
A pontatlanság a látószög csökkenésével rohamosan csökken; ugyanis az

α

-idom szélessége

P

környezetében még csak 2 méter körüli érték, a

β

-idomé pedig már 10 m körüli, és az utóbbi módosítás esetén is 5 m körüli érték. A pontatlanság növekedésének oka az ívek lapos metsződése is. A közös rész legnagyobb mérete még az utóbbi esetben is közel 30 méter.
2. A dolgozatok nagy többsége a versenyfeladat I. megoldásában az észlelő álláspontjának

u

h

koordinátáira kapott képletekből próbálta kiolvasni

u

és közvetve

h

változását

α

és

β

változásának hatására. A vizsgálatok ‐ bár többnyire lényegében helyes korlátokat adnak ‐, a két változó miatt meglehetősen bonyolultak, és több, a középiskolai tananyagot meghaladó ismeretet használnak föl. És szinte minden dolgozat figyelmen kívül hagyta vagy egészen háttérbe szorította a feladat geometriai tartalmát.
3. Néhány dolgozat hibásnak minősítette (1)-et, mert

β = 4, 65^{\circ}

esetén nincs megoldás. A

β = 4, 7^{\circ}

adatot kerekítettnek véve egyáltalán nem azt állítjuk, hogy

β

végigfut az (1) intervallumon, hiszen az észlelés helyén

β

egyetlen határozott érték. Csak ennyit állítunk: a felhasznált eszközök és módszer miatt a

4, 7^{\circ}

adat pontatlan lehet, de hibája sem fölfelé, sem lefelé nem haladja meg a

0, 5^{\circ}

-ot.

¹A versenyfeladat megoldását lásd K. M. L. 31 (1965. nov.) 104. o. Az új kérdés megoldásának megértéséhez szükséges az ottani megoldás elolvasása.

²A bemutatott ábrarész méretaránya $1 : 600$ . A teljes $P O_{1} O_{2}$ háromszög $1 : 1000$ arányú kicsinyítésben egy $50 \times 10$ cm méretű lapot igényel. A szokásos méretű körző már kicsi a nagyobb ív megrajzolásához; ez az ív rajzolható úgy, hogy egy 25 cm hosszú rajzlap‐csíkon $r_{2} / 1000$ távolságban két lyukat fúrunk egy az $O_{2}$ -be leszúrandó gombostű és ceruzánk hegye számára.