Feladat: 1428. matematika feladat Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Argyelán J. ,  Babai L. ,  Bárány I. ,  Deák Jenő ,  Domokos László ,  Gegesy F. ,  Havas J. ,  Herényi István ,  Kádas S. ,  Kiss Á. ,  Lévai F. ,  Losonci Z. ,  Nádai L. ,  Papp Z. ,  Szeredi P. 
Füzet: 1966/november, 120 - 122. oldal  PDF  |  MathML 
Témakör(ök): Rácsgeometria, Térgeometria alapjai, Feladat, Gömbi geometria
Hivatkozás(ok):Feladatok: 1965/december: 1428. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. a) Az első gömbfelület P pontjaira nézve az x, y, z koordináták négyzetösszege 100-zal egyenlő, mert ez a kifejezés adja az OP távolság négyzetét; a belső pontokra nézve pedig x2+y2+z2<100. A gömb belsejében és a felületén levő rácspontokat z koordinátájuk szerint csoportosítva számláljuk meg, más szóval a vízszintesnek vett X és Y tengelyekkel meghatározott koordinátasík fölötti magasságuk, ill. e sík alatti mélységük értéke szerint. z a -10, -9, ..., -1, 0, 1, ..., 10 értékeket veheti fel. Az így egy csoportba sorolt rácspontok egy-egy vízszintes síkban vannak. Mindegyik sík egy kört metsz ki a gömbből (1. ábra, itt a sugár 3 egység), ennek középpontja a síknak a Z tengelyen levő pontja, ami szintén rácspont, a z=±10 síkok pedig egy rácspontban érintik a gömböt, továbbá minden ilyen síkon a rácspontok ugyanúgy sorakoznak, mint az XY síkon.

 
 
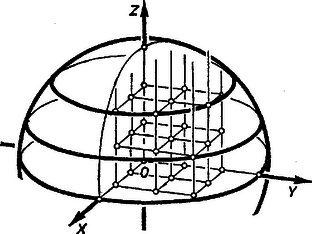1. ábra
 

Eszerint feladatunkat megoldhatjuk az 1335. feladatban végzett számlálás megismétlésével, az ottani r2 helyére az egymás utáni metszet-körök sugarának négyzetét írva, ami nyilvánvalóan 100-z2, végül a síkonként kapott N rácspont-számokat összeadva. Az egyenlő abszolút értékű z értékekhez tartozó N értékek egyenlők. A számlálások eredményét a táblázat 3. sora tartalmazza, a z>0 értékek esetében kapott N számuk összegét 2-szer és a z=0-hoz tartózót 1-szer véve a gömbben és felületén Na=4169 rácspont van (amiből 30 van a felületen).
z=109876543210r2=0193651647584919699100N=161113161197241261293293305317N'=060112164208240256284300316316   

b) A K (1/2, 1/2, 0) koordinátájú középpont körül írt r=10 sugarú gömbben ugyanezen elv szerint végzett számlálás N' eredményeit a táblázat 4. sora tartalmazza, és a keresett rácspont-szám Nb=4196 (valamennyi a gömb belsejében).
 

Az 1335. feladat megoldásához fűzött 2. megjegyzéshez hasonlóan kézenfekvő az a sejtés is, hogy a koordináta-rendszerbe egy elég nagy konvex testet helyezve, a benne levő rácspontok száma közelítőleg egyenlő a test térfogatának mértékszámával.
Gömbünk térfogata 103⋅4π/3, ebből a π-re adódó közelítő érték 3Na/4000=3,126 75, ill. 3Nb/4000=3,147.
 
Herényi Isván (Budapest, I. István g. IV. o. t.)

 
II. megoldás. A kérdéses rácspontok közül az XY sík fölöttieket a Z tengellyel párhuzamos gömbi húrok (fél-húrok) szerint csoportosítva számláljuk meg. A rácspontokat tartalmazó ilyen húrok az XY sík x2+y2=100 körében levő valamelyik (x, y) rácsponton mennek át, a gömb középpontjától mért távolságuk négyzete x2+y2, ezért fél-hosszuk négyzete 100-x2-y2, tehát a rajtuk levő rácspontok száma az ebből vont négyzetgyök egész része. A rácspontok számát megadja az ezek összegének 2-szereséből és a mondott körbeli rácspontok számából képezett összeg.
A fél-húrokon végzett számítást a szimmetriákra tekintettel elég pl. az x≥y≥0 pontokra, a kör 1/8 részében és a határoló sugarakon levő rácspontokra elvégezni, ezután a körcikk belsejében kapott rácspont-számokat 8-szor, a sugarakon találtakat 4‐4-szer kell vennünk, az origó fölöttit pedig csak 1-szer. A 2. ábra α) részén minden mondott rácspont fölé odaírtuk x2+y2 értékét, alája pedig az abból adódó rácspont-számot.
A két sugár rácspontjaihoz írt számok összege 69, ill. 48, együtt 117. A körcikk belsejében 4 rácsponthoz írtunk 9-et, 5-höz 8-at, 5-höz 7-et, 4-hez 6-ot, 5-höz 5-öt, 2-höz 4-et, 4-hez 3-at és 1-hez 1-et, ezek összege 181, ennélfogva a felső gömb belsejében és görbe felületén levő rácspontok száma 1⋅10+4⋅117+8⋅181=1926. Végül a keresett szám 2⋅1926+317=4169.
 
 
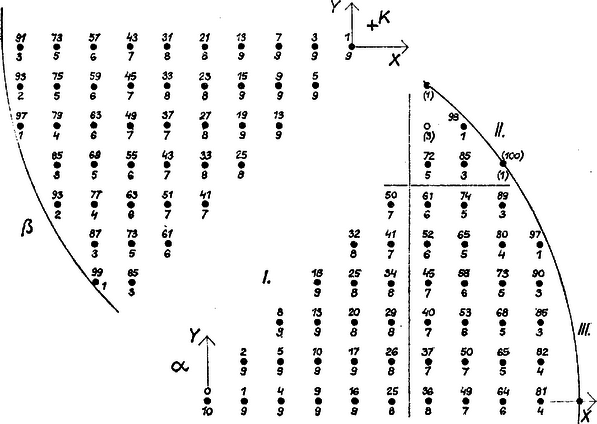2. ábra
 

A második gömb esetére a húrok K-tól mért távolságának négyzete
d2=(x-1/2)2+(y-1/2)2=x2-x+y2-y+1/2,
így a húr félhosszának négyzete 99,5-x2-y2+x+y, nem egész szám, így végpontja nem lehet rácspont. Ezért egyszerűség kedvéért a fenti mintára készült ábra rácspontjaiba d2 egészre fölkerekített értékét írtuk be (a 2. ábra β részén az (x-1/2)2+(y-1/2)2=100 körből az x≤y≤0 nyolcadrész szerepel), továbbá ismét a fél-húr rácspontjainak számát, az XY síkon levő pontot most sem számítva. A tengelyek szögfelezője menti sugáron az összeg 51, a körcikkben 217, így a félgömb belsejében 4⋅51+8⋅217=1940, és az egész gömbben 2⋅1940+316=4196.
 
Deák Jenő (Budapest, Kölcsey F. g. IV. o. t.)

 
 
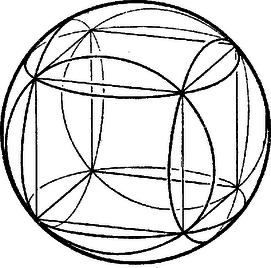3. ábra
 

Megjegyzés. Az a) esetben a 2.α ábra szerinti számítást leszűkíthetjük az I. és II. síkrészbeli pontokra, ha a gömböt a tengelyekkel párhuzamos élekkel bíró, beírt kocka lapsíkjaival az 1311. feladatban látott módon részekre osztjuk (3. ábra). A kocka élének félhossza 10/3≈5,8 egység, így egy lapsík sem megy át rácsponton. A kocka belsejében levő rácspontok száma (2⋅5+1)3=1331. 1 ‐ 1 kockalap fölötti boltozatban levő rácspontok száma az I. síkrész szerint számítható, minden fél-húr alsó 5 rácspontját lehagyva: 5+4(19+17)+8⋅33=413. Az éleknél keletkező gerezdbeli rácspontok száma pedig a II. síkrész szerint, figyelembe véve a húrok teljes hosszát, valamint az XY síkbeli kör 2 kerületi rácspontját:
11+3+2⋅7+2⋅1=30.
Mindezek szerint a rácspontok száma 1331+6⋅413+12⋅30=4169.
 
Domokos László (Tatabánya, Árpád g. IV. o. t.)