Kezdőlap


Feladat:	1422. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bod Judit
Füzet:	1966/november, 115 - 116. oldal		PDF \| MathML
Témakör(ök):	Koszinusztétel alkalmazása, Feladat
Hivatkozás(ok):	Feladatok: 1965/november: 1422. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A koszinusz-tétel fölhasználásával az $A B C$ és $A C D$ háromszögből, majd $4$ tizedesre kerekítve:

\begin{matrix} cos B A C ∢ = cos α = 61 / 72 = 0, 8472, \\ cos C A D ∢ = cos δ = 17 / 32 = 0, 5312, \end{matrix}

amiből a szögek interpolált részét közönséges törttel kifejezve, fokban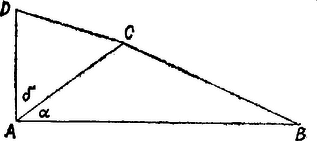

\begin{matrix} α + δ = 32, 0 + \frac{8}{90} + 57, 9 + \frac{2}{150} = 89, 9 + \frac{46}{450} = 90^{\circ} + 8'', \end{matrix}

ami Pál állítása mellett szól.

Viszont a

lg

cos táblázatot használva

\begin{matrix} log cos α = 9, 9280 - 10, \\ lg cos δ = 9, 7253 - 10, \end{matrix}

\begin{matrix} α + δ = 32, 0 + \frac{4}{50} + 57, 9 + \frac{1}{120} = 89, 9 + \frac{53}{600} = 90^{\circ} - 42'', \end{matrix}

eszerint Péternek volna igaza.
Az ellentmondás abból ered, hogy táblázatunk adatai kerekítettek, és a számításba emiatt bejutó hibák itt nagyobbak a

90^{\circ}

és

α + δ

közti, láthatóan kicsi abszolút értékű különbségnél.
A vitát eldönthetjük pl. úgy, hogy kiszámítjuk az addíció-tétel alapján

cos (α + δ)

értékét. Ha ez pozitív, akkor Péter állítása helyes, ha negatív, akkor Pálé, ha pedig

0

, akkor a kérdéses szög éppen derékszög. Ehhez

\begin{matrix} sin α = \sqrt[]{1 - cos^{2} α} = \sqrt[]{72^{2} - 61^{2}} / 72, sin δ = \sqrt[]{32^{2} - 17^{2}} / 32, \\ 72 \cdot 32 cos (α + δ) = 61 \cdot 17 - \sqrt[]{1463 \cdot 735} . \end{matrix}

Az első tag négyzete

3721 \cdot 289 = 1 075 369

, a kivonandóé

1463 \cdot 735 = 1 075 305

, kisebb amannál,

cos (α + δ) > 0

, a kérdéses szög hegyesszög.

Bod Judit (Budapest, Apáczai Csere J. gyak. g. III. o. t.)

Megjegyzések. 1. Dönthetünk az addíció-tétel fölhasználása nélkül is az

s = cos^{2} α + cos^{2} δ

összeg és

1

nagyságviszonya alapján. Ha

s ⋛ 1

, akkor

cos^{2} δ ⋛ sin^{2} α = cos^{2} (90^{\circ} - α)

, és

δ ⋚ 90^{\circ} - α

, mert pozitív hegyesszögek esetén nagyobb koszinuszértékhez kisebb szög tartozik. Esetünkben

s = (244^{2} + 153^{2}) / 288^{2} = 82 945 / 82 944 > 1

α + δ

hegyesszög.
2. Többjegyű táblázat szerint

90^{\circ} - α - δ < 3''