Feladat: 1414. matematika feladat Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Babai L. ,  Domokos L. ,  Havas János ,  Kádas S. ,  Szeredi P. 
Füzet: 1966/szeptember, 10 - 11. oldal  PDF  |  MathML 
Témakör(ök): Kombinatorikus geometria síkban, Feladat, Gráfelmélet
Hivatkozás(ok):Feladatok: 1965/október: 1414. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Nevezzük minden egyes pont rendszámának az oda befutó átmérők számát. Ha nincs 2-nél nagyobb rendszámú pont, akkor az állítás igaz, hiszen így az átmérővégződések összes száma legfeljebb 2n, és minden átmérő 2 pontba fut be.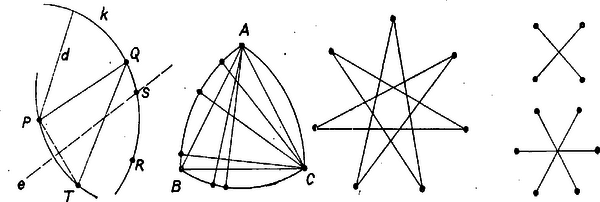

 
 

Tegyük fel, hogy az adottak közül való P pont rendszáma nagyobb 2-nél. Ekkor minden ide befutó átmérő másik végpontja a P körüli d sugarú k körön van, és egy adott pont sem fekszik k-n kívül. Legyen QR a k-nak az a legrövidebb íve, amely az összes végpontokat tartalmazza, ekkor Q és R az adott pontok közül valók, és QR≦d. Feltevésünk szerint van az ív belsejében legalább egy S pont az adott pontok közül. Állítjuk, hogy minden ilyen belső S pont rendszáma 1. Valóban, ellentmondásra jutunk azt feltéve, hogy ST egy, az SP-től különböző átmérő. Ekkor ugyanis PT-nek (S-en átmenő) e felező merőlegese elválasztja egymástól Q-t és R-et, és ha ezek közül Q van e-nek a P-t tartalmazó partján, akkor QT>QP=d, ami lehetetlen. (e csak akkor nem választaná el Q-t R-től, ha S-en kívül még egyszer metszené a mondott QR ívet; ekkor azonban T kívül esnék a k-n, ami lehetetlen.) ‐ Ezek szerint a pontrendszer minden 2-nél nagyobb rendszámú pontjából legfeljebb 2 átmérő megy olyan pontba, melynek rendszáma nagyobb 1-nél.
Hagyjuk el most átmenetileg a 2-nél kisebb rendszámú pontokat. Evvel a belőlük kiinduló átmérők is ‐ ha egyáltalán vannak ‐ elmaradnak, és bármelyik megmaradó pontból legfeljebb 2 átmérő indul ki, tehát e szűkített pontrendszerre az állítás helyes, az átmérők száma nem nagyobb a pontok számánál. Visszavéve az 1 vagy 0 rendszámú pontokat, minden ponttal együtt legfeljebb 1 átmérőt veszünk vissza, tehát az állítás igaz marad.
Bármely szóba jövő n esetére megadható n átmérőt tartalmazó pontrendszer. Ilyet alkot pl. egy ABC szabályos háromszög 3 csúcsa és n-3 olyan pont, amely A, B, C egyikétől AB-vel egyenlő, a másik kettőtől pedig kisebb távolságra van. A szabályos n-szög csúcsai rendszerének n=2k+1 esetén ugyancsak n átmérője van, n=2k esetén viszont csak n/2 a számuk, és minden pont rendje 2, ill. 1.
 
Havas János (Budapest, Berzsenyi D. g. III. o. t.)