Feladat: 1413. matematika feladat Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Argyelán János ,  Babai L. ,  Balogh K. ,  Bán P. ,  Bárány I. ,  Csernó J. ,  Deák J. ,  Domokos L. ,  Fogaras A. ,  Fövényesi Ildikó ,  Gömböcz L. ,  Havas J. ,  Herényi I. ,  Hoffmann Gy. ,  Joó I. ,  Kádas S. ,  Kiss A. ,  Lamm P. ,  Óhegyi E. ,  Szeidl L. ,  Szentgáli Á. ,  Szeredi P. ,  Tényi G. ,  Tolnay-Knefély T. 
Füzet: 1966/szeptember, 9 - 10. oldal  PDF  |  MathML 
Témakör(ök): Magasságpont, Egyenes, Feladat, Mértani helyek, Geometriai transzformációk
Hivatkozás(ok):Feladatok: 1965/október: 1413. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. a) Megmutatjuk, hogy ha M befutja az AB szakaszt, akkor H befutja az OAB háromszög AA1 és BB1 magasságainak talppontja közti A1B1 szakaszt. Ez nyilvánvaló, ha pl. a BAO szög derékszög, és így az OPQ háromszög P-ből húzott magassága azonos AA1-gyel. BAO∢≠90∘ esetén a P-ből húzott magasság párhuzamos AA1-gyel, ezért az A1B1 szakaszt mindig AP/PB1 arányban osztja ketté, és ez az arány egyenlő AM/MB-vel, mert MP∥BB1. Hasonlóan a Q-ból húzott magasság ‐ mivel párhuzamos BB1-gyel ‐ az A1B1 szakaszt mindig A1Q/QB=AM/MB arányban osztja ketté, hiszen MQ∥AA1. Eszerint a P-ből és Q-ból húzott magasság az A1B1 szakaszt ugyanazon pontban metszi, és ez a pont H, mint az OPQ háromszög két magasságának közös pontja. ‐ Amikor pedig M az A-ban, ill. B-ben van, akkor H nyilván A1-ben, ill. B1-ben adódik.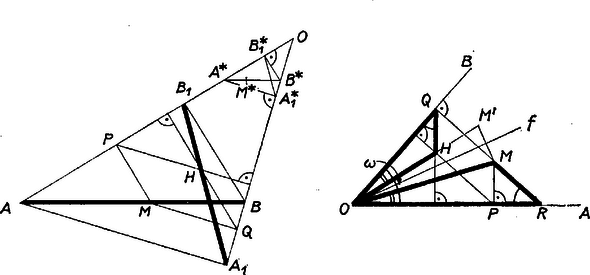

 
 

Az A1B1 szakasz bármely H pontját megkapjuk magasságpontként, éspedig az AB szakaszt AM/MB=A1H/HB1 arányban osztó M pontból indulva ki. Ezt megkaphatjuk pl. úgy, hogy a H-ból OB-re állított merőlegesnek OA-val való P metszéspontjában az OA-ra állított merőlegessel metsszük AB-t. ‐ Ezek szerint az a) esetben H mértani helye az A1B1 szakasz (a végpontjait is hozzászámítva).
 
b) A fentiekből adódik, hogy ha M befutja az OAB háromszög belsejét, akkor H mértani helye az OA1B1 háromszög belseje. Messe ugyanis az M*-on átmenő, AB-vel párhuzamos egyenes az OA, OB szakaszokat A*-ban, ill. B*-ban, akkor az OA*B* háromszög előáll az OAB-ből OA*:OA=k<1 arányú hasonlósági transzformációval, ezért míg M* befutja az A*B* szakaszt, addig a hozzá tartozó H* befutja az A*A1*, B*B1* magasságszakaszok talppontjai közti A1*B1* szakaszt (a végpontokat most már mindkét szakaszból kizárva), ez a szakasz pedig az A1B1 szakasz k arányú transzformáltja az O középpontra nézve, tehát benne van az OA1B1 háromszögben.
Az OA1B1 háromszög tetszés szerinti H* pontjához úgy kapható meg az az M*, amelyből visszajutunk H*-hoz, hogy H*-on át párhuzamost húzunk A1B1-gyel, ez metszi ki az A1*, B1* pontot, az ezekben felállított magasság A*-ot, ill. B*-ot, ekkor M* a fentiekhez hasonlóan adódik az A*B* szakaszon. ‐ Ezzel állításunkat bebizonyítottuk.
 
Argyelán János (Veszprém, Vegyip. t. IV. o. t.)

 
II. megoldás. Legyen M az AOB szögtartomány tetszés szerinti belső pontja, és messe a feladat szerinti QM egyenes az OA szárt R-ben. Így OQH∢=ORM∢, mert merőleges szárú hegyesszögek. Másrészt az OQR és MPR háromszögek hasonlósága és MPHQ paralelogramma volta miatt
OQ:OR=MP:MR=HQ:MR,
ezért az OQH és ORM háromszögek hasonlók, HOQ∢=MOR∢, és megfelelő oldalaik aránya
OH:OM=OQ:OR=cosω,
ahol ω=AOB∢.
Eszerint H-t úgy is megkaphatjuk M-ből, hogy ezt tükrözzük az AOB szög f felező egyenesére, majd a kapott M' pontra O középpontú és cosω arányú hasonlósági transzformációt alkalmazunk. ‐ Ez nyilvánvalóan akkor is helyes, ha M az AOB szögtartomány határán van.
Mind a tükrözés, mind a hasonlósági transzformáció szakaszt szakaszba, háromszögtartományt háromszögtartományba visz át, ezért ha M befutja az AB szakaszt, ill. az OAB háromszög belsejét, úgy H az A1B1 szakaszt, ill. az OA1B1 háromszög belsejét futja be, ahol A1, B1 az A, ill. B pontnak a fenti módon megszerkesztett képe, vagyis az A-ból OB-re, ill. B-ből OA-ra bocsátott merőleges talppontja.