Feladat: 1408. matematika feladat Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Babai László ,  Bárány Imre ,  Csernátony Cs. ,  Domokos László ,  Eff Lajos ,  Egri R. ,  Faragó T. ,  Gáspár András ,  Havas János ,  Herényi István ,  Kiss Árpád ,  Klocknicer Imre ,  Köves M. ,  Lévai F. ,  Losonci Z. ,  Recski A. ,  Szeidl L. ,  Szeredi Péter ,  Vincze András 
Füzet: 1967/november, 101 - 103. oldal  PDF  |  MathML 
Témakör(ök): Gráfelmélet, Kombinatorikai leszámolási problémák, Teljes indukció módszere, Feladat
Hivatkozás(ok):Feladatok: 1965/szeptember: 1408. matematika feladat

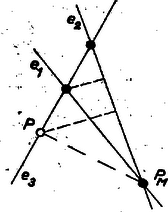
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a metszéspontokat P1,...,PM-mel, az egyeneseket e1,...,en-nel úgy, hogy Pi rendje ri legyen (i=1,...,M) és ej-n Rj darab Pi pont legyen.
Vegyük észre, hogy c)-ből és f)-ből következik, hogy

M≥n(g)
és fordítva is, c)-ből és g)-ből következik f). Ugyancsak következik c)-ből, d)-ből és g)-ből e), így elég az a) ‐ d) és g) állításokat igazolni.
I. Egy ej egyenesen végighaladva számoljuk össze kétféleképpen, hány egyenest lépünk át. Egyrészt átlépjük a többi egyenesek mindegyikét egyszer, tehát n-1 egyenest, másrészt az egyes egyeneseken minden Pi pontban ri-1 egyenest lépünk át. Eszerint az egy egyenesen levő Pi pontokra az ri-1 értékek összege n-1.
a) Megállapításunkból következik, hogy az egy egyenesen levő Pi-kre az ri-1-ek közt a páratlanok ‐ vagyis az egyenesen levő páros rendű pontok száma ‐ páros, ha n-1 páros, vagyis ha n páratlan, és a mondott szám páratlan, ha n páros.
b) A fenti megszámlálást minden egyenesen elvégezve egyrészt n(n-1) átlépést számlálunk, ez áll b) jobb oldalán; másrészt minden Pi ponton ri-szer haladunk át és minden alkalommal ri-1 átlépést, tehát összesen ri(ri-1) átlépést számolunk össze, tehát pontok szerint számolva össze b) bal oldalát kapjuk. Ezzel az összefüggést igazoltuk.
c) Most számoljuk össze az egyes egyenesek mentén levő Pi pontokat. Minden egyenesen végigmenve éppen c) bal oldalát kapjuk. Másrészt egy Pi pontot minden rajta átmenő egyenesen számba vettünk egyszer, összesen tehát ri-szer számoltuk. Így pontok szerint csoportosítva a jobb oldalt kapjuk. Ezzel ezt az egyenlőséget is igazoltuk.
Idáig nem használtuk fel azt a feltevést, hogy nem halad át egy közös ponton minden egyenes, az a) ‐ c) állítás tehát erre az esetre is érvényes (csak triviális).
d) és g) igazolásához szükségünk van arra a segédtételre, hogy ha az egyenesek nem egy ponton mennek keresztül, akkor van olyan metszéspont, mondjuk PM, amire rM=2. Ebből a két állítás az alábbiak szerint következik.
d) Legyen a PM-en átmenő egyenes e1 és e2. Megszámolva e1-en és e2-n az egyenes-átlépések számát és hozzászámolva még a metszéspontok számát is PM kivételével, egyrészt 2(n-1)+M-1-et kapunk, ami az összefüggés jobb oldala. Másrészt PM-et 2=rM-szer vettük számításba (mind e1-en, mind e2-n egy átlépés történt PM-ben), az e1-en és e2-n levő Pi-k mindegyikében ri-1 átlépést számoltunk és egyszer a pontot számba vettük, így ezek a pontok ri-vel járultak az összeghez; egy sem e1-en, sem e2-n nem levő Pi pont pedig, ha van ilyen, 1-szer van számba véve, vagyis kevesebbszer, mint a rendje. Ezzel az egyenlőtlenséget igazoltuk.
Azt is látjuk, hogy d)-ben akkor és csak akkor áll fenn egyenlőség, ha nincs metszéspont a fenti e1, e2 egyenespáron kívül. Könnyű belátni, hogy ez csak úgy lehetséges, ha egyikükön ‐ mondjuk e2-n ‐ csak egy a PM-től különböző metszéspont van, ezen minden egyenes átmegy, kivéve e1-et, továbbá azt is, hogy ekkor M=n.
g) Teljes indukcióval bizonyítjuk az állítást. 3 egyenes esetén M=n=3. Tegyük fel, hogy n-1 egyenesre igaz az állítás és vegyünk a feltételeknek megfelelő n egyenest, ezeknek egy másodrendű PM metszéspontját, melyen átmegy az e1 egyenes. Elhagyva e1-et, PM megszűnik metszéspont lenni és minden további, az e1-en levő másodrendű metszéspont is, ha van ilyen. Így a megmaradó egyenesek metszéspontjainak M' száma legfeljebb M-1. Ha a megmaradó egyenesek egy ponton mennek keresztül, akkor nyilván e1-gyel elmetszve őket összesen M=n metszéspont lesz. Ha nem mennek mind át egy ponton, akkor érvényes rájuk az állítás, vagyis
M-1≥M'≥n-1,amibőlM≥n.
Így g) igaz akárhány egyenesre.
II. Bebizonyítjuk a d) és g) igazolásában felhasznált segédtételt, vagyis hogy feltevéseink mellett van olyan metszéspont, melynek rendje 2, más szóval amely az adott n egyenes közül pontosan kettőn van rajta. * Tekintsük mindegyik ej távolságát mindegyik olyan Pi-től, mely nincs rajta. Legyen e távolságok legkisebbike ‐ az indexeket alkalmasan választva ‐ e3 távolsága PM-től. Ekkor PM-en két ej megy át.
 
 

Legyen ugyanis P a PM-ből e3-ra bocsátott merőleges talppontja. Ha PM-en három ej menne át, akkor P valamelyik oldalán legalább két ilyen egyenes metszené e3-at, legyenek ezek e1 és e2 úgy, hogy e1 a PMP és e2 egyenes közti hegyesszög-tartományban halad; esetleg e1 egybeesik PMP-vel. Ekkor e2 távolsága e1 és e3 metszéspontjától kisebb lenne, mint PMP, hiszen nem lehetne nagyobb, mint az e3, PMP és e2 egyenesekkel meghatározott derékszögű háromszögnek az átfogóra merőleges magassága, PMP viszont nagyobb ennél. Ezek szerint PM-en valóban nem mehet át 2-nél több ej.
 

Megjegyzések. 1. Fent csak g)-t bizonyítottuk teljes indukcióval. Ugyanígy bizonyíthatók az előző állítások is. Érdekes, hogy d) teljes indukciós bizonyítása nem használja fel a fenti mélyebb segédtételt.
2. Meg lehet mutatni, hogy M=n csak a mondott speciális alakzatra teljesül. g) helyett a következő élesebb állítás is bizonyítható teljes indukcióval: M>n, kivéve ha elhagyható egy egyenes úgy, hogy a többi egy ponton menjen keresztül, ekkor M=n.
Ha n=3, akkor csak a kivételes eset állhat elő, bármelyik egyenes lehet az elhagyandó. A kivételes esetben nyilvánvalóan M=n. Legyen most n>3, n-1-re legyen igaz az állítás, legyen n egyenesünk, amely megfelel a feltételeknek és nem a kivételes esetet mutatja. A segédtétel szerint van olyan e1 egyenes, amelyen van másodrendű pont. Ha e1 elhagyása után sem a kivételes eset áll elő, akkor M-1≥M'>n-1, s így M>n. Ha a kivételes eset jön létre, akkor e1 nem mehet át olyan metszésponton, amin rajta kívül n-2 egyenes megy át, de ekkor legalább 2 egyenest metsz olyan pontban, amin harmadik egyenes nem megy át, s így M-1>M'=n-1, tehát M>n. Az élesebb állítás is igaz tehát akárhány egyenesre.
*A segédtétel rokon Gallai Tibor következő tételével: ,,legyen adva a síkban n pont, melyek nincsenek mind egy egyenesen, ekkor van olyan egyenes, mely ezen n pont közül pontosan kettőn megy át'' ‐ és ebből a tételből segédtételünk az ,,egyenes'' és ,,pont'', továbbá ,,metszés'' és ,,összekötés'' szó-párok egymással való kicserélése (és a szükségessé váló stiláris módosítások) útján keletkezik. Két ilyen tételt egymás duálisának mondunk.