Kezdőlap


Feladat:	1407. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Arányi P. , Babai L. , Bárány I. , Cserháti Zsuzsa , Deák J. , Domokos L. , Eff L. , Egri R. , Fürész J. , Füvesi I. , Havas J. , Herényi I. , Herszényi B. , Hoffmann Gy. , Iváncsy Sz. , Juhász F. , Kafka P. , Kelle P. , Lamm P. , Langer T. , Legányi A. , Lelkes A. , Major Pál , Moczok L. , Óhegyi E. , Pethő I. , Rácz M. , Recski A. , Rosta L. , Sarkadi Nagy I. , Sólymos L. , Steiner Gy. , Szabó I. , Szalay S. , Szentgáli Á. , Szeredi P. , Szilágyi P. , Takács László , Tóth A.
Füzet:	1966/május, 206 - 207. oldal		PDF \| MathML
Témakör(ök):	Terület, felszín, Síkgeometriai számítások trigonometria nélkül körökben, Feladat
Hivatkozás(ok):	Feladatok: 1965/szeptember: 1407. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A körlemezek $r$ sugara nem lehet nagyobb annál a $R$ értéknél, amelynek esetében az 5. lemez a többi $4$ mindegyikét érinti. Ekkor a négyzet átlója ‐ a) ábrarész ‐

\begin{matrix} \sqrt[]{2} = 2 \sqrt[]{2} R + 4 R, amiből az átmérő : 2 R = \sqrt[]{2} - 1 (\approx 0, 414) . \end{matrix}

Így az 5. lemez nem mozoghat, a súrolt terület

π R^{2}

.
A súrolt rész számítása kétféleképpen alakul aszerint, hogy az 5. lemez érintheti-e a négyzet oldalait vagy sem. Az érintés nyilvánvalóan

r \leq 1 / 6

esetén lép fel. Mindkét esetben a nem súrolt rész területét számítjuk ki, mindig kihasználva a négyzet szimmetriáit.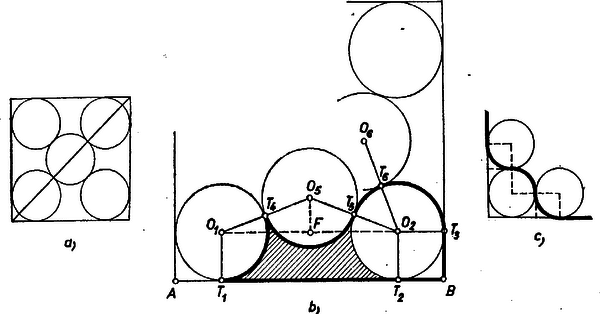

1 / 6 \leq r \leq R

esetén a nem súrolt rész

1 / 4

része a b) ábrarész vastag vonallal határolt idoma, területe a vonalkázott idom, az

O_{2}

közepű kör és a

B T_{2} T_{3}

idom területének összege. Az első kettő összege egyenlő a

T_{1} T_{2} O_{2} O_{5} O_{1}

ötszög területével. Ugyanis a vonalkázott idom az ötszögből az

O_{1} T_{1} T_{4}

O_{2} T_{2} T_{5}

és

O_{5} T_{4} T_{5}

körcikkek elhagyásával áll elő, ezek területének összege pedig egyenlő a kör területével, mert középponti szögeik összegét az ötszög szögeinek összegéből a

T_{1}

-nél és

T_{2}

-nél levő szögek összegének elhagyásával kapjuk, és így a maradék

360^{\circ}

. Az ötszöget az

O_{1} O_{2}

átló egy

r (1 - 2 r)

területű téglalapra és az

O_{1} O_{2} O_{5}

egyenlő szárú háromszögre bontja. Ennek alapja

1 - 2 r

, magassága

\begin{matrix} \sqrt[]{O_{1} O_{5}^{2} - O_{1} F^{2}} = \sqrt[]{4 r^{2} - {(\frac{1}{2} - r)}^{2}} = \frac{1}{2} \sqrt[]{12 r^{2} + 4 r - 1} . \end{matrix}

Végül a

B T_{2} T_{3}

idom területe az

r

oldalú négyzet és az

r

sugarú negyedkör területének különbsége.
Mindezt

4

-szer véve a nem súrolt rész területe

\begin{matrix} 4 r (1 - 2 r) + (1 - 2 r) \sqrt[]{12 r^{2} + 4 r - 1} + (4 - π) r^{2}, \end{matrix}

a súrolt rész területe pedig, kellő alakítás után

\begin{matrix} {(1 - 2 r)}^{2} + π r^{2} - (1 - 2 r) \sqrt[]{12 r^{2} + 4 r - 1} . \end{matrix}

II.

r \geq 1 / 6

esetén a nem súrolható rész a négyzet mindegyik csúcsa környezetében egy körre és

5

, a fenti

B T_{2} T_{3}

idomhoz hasonló idomra bontható ‐ c) ábrarész ‐, így a súrolt rész területe

\begin{matrix} 1 - 4 [π r^{2} + 5 (r^{2} - \frac{π r^{2}}{4})] = 1 - (20 - π) r^{2} . \end{matrix}

r = 1 / 6

esetén mindkét kifejezés megadja a keresett értéket, a fentebbi háromszögek egyenes szakasszá laposodnak.

Takács László (Sopron, Széchenyi I. g. II. o. t.)