Kezdőlap


Feladat:	1406. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Arányi P. , Babai László , Balázs Katalin , Bárány I. , Barcza Gyöngyi , Bihari Katalin , Bottyán I. , Deák J. , Dékány I. , Domokos L. , Eff Lajos , Élthes Eszter , Fái Gy. , Fogács P. , Fogaras A. , Herényi I. , Hoffmann Gy. , Juhász F. , Kádas S. , Kafka P. , Kalmár István , Kelle P. , Kiss Á. , Korchmáros Gábor , Lamm P. , Lelkes A. , Lévai F. , Óhegyi E. , Palla L. , Pintér János , Rácz M. , Rimóczy P. , Solymosi A. , Solymosi András , Szabó István , Szeidl L. , Szentgáli Á. , Szeredi P. , Sziklai P. , Takács Ágnes , Varga Gabriella , Verdes S. , Zeisler J.
Füzet:	1966/október, 55 - 58. oldal		PDF \| MathML
Témakör(ök):	Háromszögek szerkesztése, Háromszög nevezetes körei, Feladat
Hivatkozás(ok):	Feladatok: 1965/szeptember: 1406. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. I. Tekintsük először a két oldal összegének esetét, legyen $A B C$ a keresett háromszög, $B C = a$ az adott oldal, $m_{a}$ az adott magasság, és $B A + A C = c + b = e$ , az adott összegszakasz (1. ábra). Forgassuk rá $C$ -t az $A$ körüli $k_{0}$ körrel $B A$ -nak $A$ -n túli meghosszabbítására a $C'$ pontba, ekkor $C'$ a $B$ körüli $e$ sugarú $k$ körön is rajta van, és $k$ a $C'$ -ben érinti $k_{0}$ -t. Továbbá rajzoljuk meg az $A$ -n átmenő, $B C$ -vel párhuzamos $g$ egyenest, ez szimmetriatengelye $k_{0}$ -nak, így $k_{0}$ átmegy $C$ -nek $g$ -re való $C_{0}$ tükörképén is.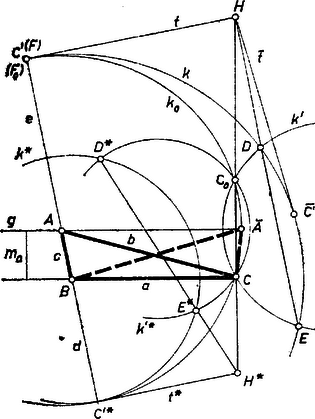

1. ábra

Minthogy a

B C

alapot felvéve

k

g

és

C_{0}

megszerkeszthetők, a feladatot visszavezettük a

k

-t érintő és a

C

C_{0}

pontokon átmenő

k_{0}

kör megszerkesztésére, ennek középpontja lesz a hátra levő

A

csúcs.

k_{0}

-nak

k

-val való

C'

érintkezési pontját fogjuk meghatározni közös

t

érintőjük és a

C C_{0}

egyenes metszéspontjának kitűzése útján, ekkor az innen

k

-hoz húzott érintő megadja

C'

-t, és

A

-t

B C'

metszi ki

g

-ből.
Legyen egy a

C

-n és

C_{0}

-on átmenő és

k

-t két különböző pontban metsző kör

k'

k

-val közös pontjai

D

E

, és a

C C_{0}

D E

egyenesek közös pontja

H

. Megmutatjuk, hogy

H

rajta van

t

-n, ez a keresett pont. Legyen

k

-nak és

k_{0}

-nak a

H C'

egyenessel való további közös pontja

F

, ill.

F_{0}

, és alkalmazzuk a kör két szelőjén a metszéspontok között keletkezett szakaszokra ismert tételt a

H

pontra és rendre a

k

k'

k_{0}

körre:

\begin{matrix} H C' \cdot H F = H D \cdot H E = H C \cdot H C_{0} = H C' \cdot H F_{0} . \end{matrix}

(1)

A szélső tagokból

H F_{0} = H F

, ezért

F_{0}

azonos

F

-fel, tehát

C'

-vel is, mert ez

k

és

k_{0}

egyetlen közös pontja, ennélfogva

H C'

azonos a keresett

t

-vel,

C'

H

-ból

k

-hoz húzott (egyik) érintő érintési pontja.
(

F_{0}

és

F

azonosságának bizonyításában azt is felhasználtuk, hogy mindkettő a

H

-nak ugyanazon oldalán van. Ez abból következik, hogy

C

, vele

k_{0}

és vele

C_{0}

is a

k

-ban van, hiszen

B C < e

, ezért a

C C_{0}

szakasz része a

C C_{0}

egyenes

k

-ba eső húrjának, ezért

D

és

E

C C_{0}

egyenes ugyanazon partján vannak, és így

H

mindhárom körre nézve külső pont.)
A visszavezetéssel kapott problémát megoldottuk, és ezzel az eredetit is. Csak azt kell még megjegyeznünk, hogy

k'

középpontját tetszés szerint választhatjuk, mert az adódó

D E

egyenes mindig ugyanabban a pontban metszi

C C_{0}

-t, hiszen ez a metszéspont azonos

t

és

C C_{0}

, metszéspontjával,

H

-val. ‐ Ezek után

C'

kitűzése alapszerkesztés.
A szerkesztés helyességének bizonyítására csak azt kell belátnunk, hogy a

H

-hól

C'

útján a fentiek szerint kapott

A

pontra nézve fennáll

A C = A C'

. Valóban, az

A

körül

A C

sugárral írt kört

H C

még egyszer

C_{0}

-ban metszi, és

H C \cdot H C_{0} = H C^{' 2}

, eszerint a kört

C'

-ben érinti

H C'

, tehát

A C'

hossza a sugár.
A szerkesztés végrehajtható, ha

C_{0}

k

belsejében vagy a kerületén adódik:

B C_{0} \leq e

, azaz

a^{2} + 4 m_{a}^{2} \leq e^{2}

, ez magában foglalja az

a < e

feltételt is. Egyenlőség esetén

C_{0}

k

-n van, ide esik

H

és

C'

, tehát csak egy háromszög adódik; ekkor

A

felezi

B C_{0}

-t, az

A B C

háromszög egyenlő szárú:

B A = A C_{0} = A C

k

belsejében létrejött

C_{0}

esetén viszont

H

külső pont, két érintő húzható belőle, két háromszög adódik; bennük

A C

és

A B

különbözők, mert

C'

egyik helyzete közelebb van

g

-hez, mint

C_{0}

, másika távolabb (de mindenesetre

g

-nek

B

-t nem tartalmazó partján). Másrészt eleve tudjuk, hogy egy megoldásnak

B C

felező merőlegesére való tükörképe is megoldás, ezért a kapott két megoldás nem lényegesen különböző.

II. Adott két oldal különbsége: az

A C - A B = b - c = d

szakasz. Fenti megoldásunk csekély módosítással ismét használható lesz. Az

A C'^{*} = A C

szakaszt az

A B

félegyenesre mérjük fel, így

B C'^{*} = d

, tehát

C'^{*}

B

körüli,

d

sugarú

k^{*}

körön lesz, és lényegében

C'^{*}

megszerkesztését tekintjük feladatunknak. A

C

C_{0}

pontokon átmenő, alkalmas

k'^{*}

kör által most a

k^{*}

-ból kimetszett

D^{*}

E^{*}

pontokat összekötő szelő metszi ki

C C_{0}

-ból azt a

H^{*}

pontot, ahol

k^{*}

-nak

C'^{*}

-beli

t^{*}

érintője is átmegy, vagyis amely

H^{*}

-ból húzott érintő érintési pontja adja

C'^{*}

-ot.
A szerkeszthetőség egyetlen feltétele

d < a

. Így ugyanis

C

k^{*}

-ra nézve külső pont, és ez áll a

C C_{0}

egyenes minden pontjára, hiszen éppen

C

k^{*}

-hoz legközelebbi pontja. Ezért

H^{*}

nem lehet rajta

k^{*}

-on, mindig 2 érintőt, 2 megoldást kapunk, de ezek ismét szimmetrikus párt adnak (a tükörkép-megoldásban

c - b = d

).
Az elemzés, bizonyítás és diszkusszió teljes végrehajtását az olvasóra hagyjuk.

Pintér János (Budapest, I. István g. IV. o. t.)
Solymosi András (Budapest, Petőfi S. g. IV. o. t.)

Megjegyzés. Rövidebben fogalmazhatjuk megoldásainkat a pontnak körre vonatkozó hatványára, két kör közös hatványvonalára, három kör közös hatványpontjára vonatkozó fogalmak és ismeretek fölhasználásával.¹ A keresett

k_{0}

és az adott

k

(ill.

k^{*}

) érintkezési pontjában közös lesz az érintőjük, ez a

h

hatványvonaluk.

C

és

C_{0}

pontjainkat a

C C_{0}

egyenes útján kapcsolhatjuk össze a hatványvonallal: keressük meg

h

-nak ezen levő pontját.

C C_{0}

is hatványvonallá lesz, ha vesszük a fenti

k'

-t (ill.

k'^{*}

-ot), és ekkor

k

és

k'

hatványvonala megszerkeszthető,

C C_{0}

-ból kimetszi a

k

k_{0}

k'

körhármas

H

hatványpontját, itt megy át

h

, és érinti

k

-t.

II. megoldás (vázlat). Az

a

és

m_{a}

szakaszokból ismert a háromszög

t

területe, az

e + a

összeg pedig a

2 s

kerület, így könnyen megszerkeszthető az

A B C

háromszögbe beírható

k

kör sugarának

ϱ

, valamint az

a

oldalhoz hozzáírt

k_{a}

külső érintő kör sugarának

ϱ_{a}

hossz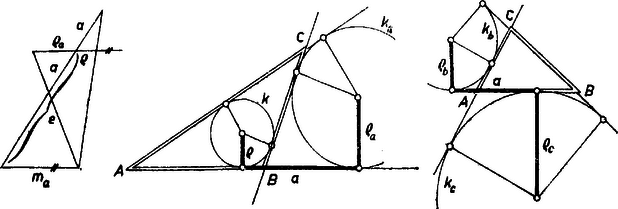a, a

\begin{matrix} ϱ = \frac{t}{s} = \frac{2 t}{2 s} = \frac{a m_{a}}{e + a}, ϱ_{a} = \frac{t}{s - a} = \frac{2 t}{2 s - 2 a} = \frac{a m_{a}}{e - a} \end{matrix}

ismert összefüggések alapján (2. ábra bal fele). Ismeretes továbbá, hogy

ϱ

és

ϱ_{a}

első kifejezésének

s

, ill.

s - a

nevezője éppen az

A

csúcs távolsága

k_{a}

-nak, ill.

k

-nak az

A B

egyenesen levő érintési pontjaitól, és e két pont

A

-nak ugyanazon oldalán van; így az ugyanazon oldalegyenesen levő érintési pontok távolsága

s - (s - a) = a

2. ábra

Ezek alapján egy

a^{*}

egyenes

a

hosszúságú szakaszának végpontjaiban emelt merőlegesekre (az egyenes ugyanazon partján)

ϱ

-t, ill.

ϱ_{a}

-t felmérve megrajzolhatjuk

k

-t és

k_{a}

-t, ezek másik közös külső érintője és bármelyik belső közös érintője

a^{*}

-gal együtt adja a keresett háromszög oldalegyeneseit (az ábra közepe).
A

b - c = d

különbség alapján a

b

és

c

oldalhoz hozzáírt

k_{b}

, ill.

k_{c}

, külső érintő kör

ϱ_{b}

ϱ_{c}

sugarát szerkeszthetjük meg:

\begin{matrix} ϱ_{b} = \frac{t}{s - b} = \frac{2 t}{a - b + c} = \frac{a m_{a}}{a - d}, ϱ_{c} = \frac{t}{s - c} = \frac{a m_{a}}{a + b}, \end{matrix}

s - b

és

s - c

e körök

A B

-n levő érintési pontjának távolsága

A

-tól,

A

e két pont között van, így távolságuk

(s - b) (s - c) = a

. A szerkesztés csak annyiban tér el az előzőtől, hogy a két kört

a^{*}

két partján kell rajzolnunk, a háromszög oldalegyenesei

a^{*}

, a körök másik belső közös érintője (ami itt biztosan létezik), és bármelyik a közös külső érintőik közül.
A bizonyítás és a diszkusszió végrehajtásával az olvasó könnyen teljes megoldássá egészítheti ki vázlatainkat.

Korchmáros Gábor (Budapest, Rákóczi F. g. IV. o. t.) dolgozata alapján kiegészítésekkel

Megjegyzések. 1. A

B C

oldalt rögzítve az

A

csúcs egyrészt a

B C

-val párhuzamos, tőle

m_{a}

távolságban haladó

g

egyenesen van rajta, másrészt azon az ellipszisen, ill. hiperbolán, melynek fókuszai

B

és

C

, és nagy tengelye

e = b + c

, ill. valós tengelye

d = | b - c |

. E két mértani hely közös pontjainak megszerkesztését könnyíti, hogy

g

párhuzamos a görbe egyik tengelyével. A szerkesztést az 1325. feladat² ellipszis esetére vázolta, hiperbola esetére végrehajtotta. Mindkét görbe

O

középpontja

B C

felezőpontja, az ellipszis kis tengelyének

L

végpontjára

B L = C L = e / 2

. Messe

g

O

körüli

O L

sugarú

k

(kis-) kört

M

-ben, az

O M

félegyenes az

O

körüli,

e / 2

sugarú

n

(nagy-) kört

N

-ben, ekkor az

A

csúcsot az

N

-ből

B C

-re bocsátott merőleges metszi ki

g

-ből (3. ábr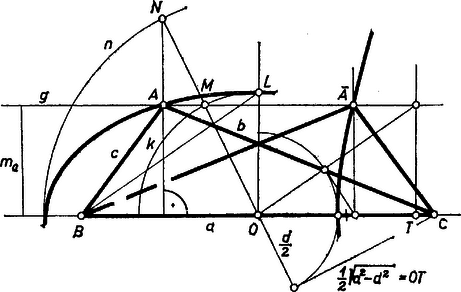a).

3. ábra

Eff Lajos (Budapest, Fazekas M. gyak. g. III. o. t.)

2. A szerkesztést számítással többféleképpen is előkészíthetjük. Pl. a Heron-képlet alapján:

\begin{matrix} 16 t^{2} = 4 a^{2} m_{a}^{2} = (e + a) (e - a) (a + d) (a - d), \end{matrix}

e

és

d

mindegyikéhez megszerkeszthetjük a másikat.

Kalmár István (Debrecen, Fazekas M. g. IV. o. t.)

¹Lásd pl. Gallai T.‐Hódi E.‐Péter R.‐Szabó P.‐Tolnai J.: Matematika a gimn. III. o. számára, 12. kiadás, Tankönyvkiadó, Bp. 1962, 197‐200. o.

²K. M. L. 30 (1965) 207. o.