|
| Feladat: |
1405. matematika feladat |
Korcsoport: 18- |
Nehézségi fok: nehéz |
| Megoldó(k): |
Babai L. , Bajna Zs. , Bárány I. , Bod Judit , Cserháti Zsuzsa , Csikós Miklós , Domokos L. , Egri R. , Fogaras A. , Forgács P. , Füvesi I. , Gárdos Eszter , Gáspár A. , Herényi I. , Kádas S. , Kalmár István , Kelle P. , Kiss A. , Kloknicer I. , Komlósi S. , Lévai F. , Major Pál , Pintér M. , Rimóczy P. , Rodler Erzsébet , Sarkadi Nagy I. , Schwanner I. , Szeidl L. , Szeredi P. , Szilágyi P. , Tolnay-Knefély T. |
| Füzet: |
1966/március,
111 - 113. oldal |
 PDF | PDF |  MathML MathML |
| Témakör(ök): |
Ellipszis egyenlete, Kúpszeletek érintői, Feladat |
| Hivatkozás(ok): | Feladatok: 1965/szeptember: 1405. matematika feladat |
|
|
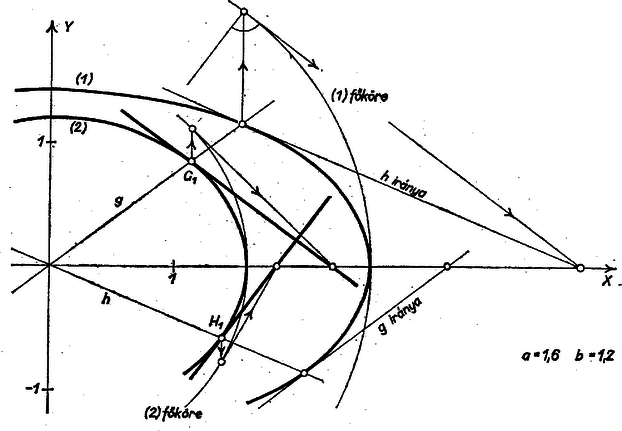
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A koordinátageometria eljárásával követjük az ellipszis előírt pontjához tartozó érintő megszerkesztésére az idézett tankönyv 44. oldalán közölt eljárást: az ellipszis előírt pontján át a nagy tengelyre merőleges egyenessel metsszük a főkört (az ellipszis középpontja körül a nagy tengely felével mint sugárral írt kört), a metszéspontban a főkörhöz húzott érintőn vesszük a nagy tengely meghosszabbításával való metszéspontot, ezt az előírt ponttal összekötő egyenes az ellipszis keresett érintője.
Legyen a egyenes egyenlete , (, hiszen a tengelyekre vonatkozóan az állítás nyilvánvalóan igaz.) -nek a (2) ellipszissel való metszéspontja és . koordinátái: | | (3) |
-nek a pozitív abszcisszájú metszéspontot véve. A (2) ellipszis főkörének egyenlete (feltettük, hogy ), ezt a kört a -en átmenő, az -re merőleges egyenes az ordinátájú pontjában metszi (a két metszéspont bármelyike használható). A főkör ezen pontjában húzott érintő egyenlete, majd az -tengellyel való metszéspontjának abszcisszája | |
és így az összekötő egyenes iránytényezője, felhasználva a (3) eredményeket | | (4) |
ez a -ben húzott érintő iránytényezője.
A -re vonatkozó számítás ettől csak abban tér el, hogy és helyére a negatívjuk lép, a végeredmény azonban (4) harmadik alakja szerint ugyanaz, tehát az ellipszis bármely átmérőjének végpontjaiban az érintők párhuzamosak.
(4)-ben egyszersmind összefüggést kaptunk (2) két konjugált átmérőjének iránytényezői között. Ebből a -hez az (1) ellipszisben hozzá konjugált átmérő, vagyis a egyenes iránytényezőjét úgy kapjuk, hogy , helyére (1) féltengelyeinek mértékszámát írjuk, azaz -et, ill. -et: Ennek alapján a -ben és -ben húzott érintők iránytényezőjét, újabb számítás nélkül (4)-ből úgy kapjuk, hogy helyére -t írjuk.
Most már kiszámíthatjuk a -beli és a -beli érintő iránytényezőjének szorzatát. (5) figyelembevételével | |
eszerint az érintők valóban merőlegesek.
Csikós Miklós (Budapest, Vasútgép. t. IV. o. t.)
Kalmár István (Debrecen, Fazekas M. g. IV. o. t.)
Megjegyzés. Az ellipszis érintőjének iránytangensét meghatározhatjuk pl. ahhoz az eljáráshoz hasonlóan, ahogyan a tankönyv a parabola érintőjének iránytényezőjét meghatározta. Keressük a (2) ellipszishez az tengely ‐ ahol ‐ pontjából húzott érintőt. A -n át húzott egyenes egyenletében az iránytényezőt úgy választjuk, hogy az kiküszöbölésével adódó egyenlet diszkriminánsa 0 legyen. Az érintő egyenletére a számítás végül az alakot adja, ahol az érintési pont koordinátái.
Gallai T.‐ Hódi E.‐Péter R. ‐Szabó P.‐Tolnai J.: Matematika az ált. gimn. III. o. számára, 12. kiad., Tankönyvkiadó, Bp. 1962. 204‐206. o. |
|
 PDF |
PDF |  MathML
MathML