Kezdőlap


Feladat:	1400. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bárány I. , Baranyai Zs. , Blaskó G. , Deák J. , Domokos L. , Domokos Zsuzsanna , Elekes György , Fodor Magdolna , Gáspár A. , Herényi I. , Höss Rozália , Kalmár I. , Karsai Kornélia , Kotsis Erzsébet Kinga , Lábadi A. , Lévai F. , Malina J. , Márki László , Molnár Ágnes , Nagy Klára , Sátori Gabriella , Szántó O. , Szeidl L. , Székely G. , Vesztergombi Katalin
Füzet:	1967/február, 57 - 58. oldal		PDF \| MathML
Témakör(ök):	Egyenes körhengerek, Határozott integrál, Térfogat, Feladat
Hivatkozás(ok):	Feladatok: 1965/május: 1400. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A két tengely által meghatározott $S$ sík mindkét hengernek szimmetriasíkja, így közös részüknek is. Ezért ‐ $S$ -et vízszintesen tartva ‐ elég meghatározni a $K$ közös rész $S$ fölé eső felének térfogatát.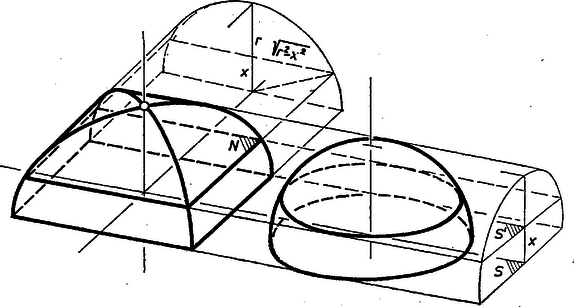

Egy az

S

-sel párhuzamos, fölötte

x (< r)

magasságban haladó

S'

sík mindkét hengert két alkotóban metszi, távolságuk

2 \sqrt[]{r^{2} - x^{2}}

, ezért a

K

-ból kimetszett idom egy ugyanekkora oldalú

N

négyzet, és területe

4 (r^{2} - x^{2})

. Az

x = r

magasságban haladó sík pedig egy‐egy alkotóban érinti a hengereket. Legyen

x

értéke egymás után

\begin{matrix} \frac{r}{n}, \frac{2 r}{n} ..., \frac{(n - 1) r}{n}, \end{matrix}

ez az

n - 1

sík

K

fölső felét

n

rétegre osztja, mindegyik réteg magassága

r / n

. Az alsó réteg alapidoma a fentihez hasonló meggondolás szerint

2 r

oldalú négyzet, a fölső rétegnek csak egyetlen pontja van az alaplapjától

r / n

távolságban, a mondott érintési alkotók metszéspontja.
Írjunk mindegyik rétegbe is és köréje is hasábot, melynek alapidoma a réteg fölső, ill. alsó határlapja; a fölső rétegbe nem lehet ilyen hasábot beírni. Minden egyes réteg benne van a köréje írt hasábban, másrészt magában foglalja a beírt hasábot, ezért térfogata e két hasáb térfogata közé esik. Így

K

fölső felének

V / 2

térfogata közéje esik a körülírt, ill. a beírt hasábok térfogatából képezett

S_{n}

, ill.

s_{n}

összegnek:

\begin{matrix} s_{n} < V / 2 < S_{n} . \end{matrix}

(

s_{n}

csak

n - 1

tagból áll.) Ezekből az összegekből a közös

r / 4

magasságot kiemelve a zárójelben a fölső, ill. alsó határlapok területének összege áll, ezért a négyzetszámok összegére ismert

\begin{matrix} 1^{2} + 2^{2} + ... + k^{2} = \frac{1}{6} k (k + 1) (2 k + 1) \end{matrix}

képlet fölhasználásával így alakíthatók:

\begin{matrix} s_{n} = \frac{r}{n} [4 (r^{2} - \frac{r^{2}}{n^{2}}) + 4 (r^{2} - \frac{4 r^{2}}{n^{2}}) + ... + 4 (r^{2} - \frac{{(n - 1)}^{2} r^{2}}{n^{2}})] = \\ = \frac{r}{n} [4 (n - 1) r^{2} - \frac{4 r^{2}}{n^{2}} (1^{2} + 2^{2} + ... + {(n - 1)}^{2})] = \\ = \frac{4 r^{3}}{n} [(n - 1) - \frac{(n - 1) (2 n - 1)}{6 n}] = 4 r^{3} \cdot \frac{(n - 1) (4 n + 1)}{6 n^{2}} = 4 r^{3} \cdot \frac{4 n^{2} - 3 n - 1}{6 n^{2}}, \\ S_{n} = S_{n} + \frac{r}{n} \cdot 4 r^{2} = 4 r^{3} [\frac{1}{n} + \frac{(n - 1) (4 n + 1)}{6 n^{2}}] = 4 r^{3} \cdot \frac{4 n^{2} + 3 n - 1}{6 n^{2}}, \end{matrix}

hiszen az alsó határlapok területének összegében ugyanúgy benne van a közbülső metszetek területének összege, mint

s_{n}

-ben, de többletként szerepel az alsó réteg alsó határlapjának

4 r^{2}

területe. Ezeket (1)-be beírva, majd

8 r^{3}

-nel osztva

\begin{matrix} \frac{4 n^{2} - 3 n - 1}{12 n^{2}} < \frac{V}{16 r^{3}} < \frac{4 n^{2} + 3 n - 1}{12 n^{2}}, azaz \\ \frac{1}{3} - \frac{3 n + 1}{12 n^{2}} < \frac{V}{16 r^{3}} < \frac{1}{3} + \frac{3 n - 1}{12 n^{2}} . \end{matrix}

Eszerint a

V / 16 r^{3}

hányados minden pozitív egész

n

esetén a bal és jobb oldali korlát közé esik. Ámde közéjük esik az

1 / 3

szám is. Végül csak egy szám van, amelyik minden pozitív egész

n

esetén a két korlát közé esik, mert különbségük,

6 n / 12 n^{2} = 1 / 2 n

, bármilyen kicsi pozitív számnál kisebb, amint

n

elég nagy. Ezért

\begin{matrix} \frac{V}{16 r^{3}} = \frac{1}{3}, V = \frac{16 r^{3}}{3} = \frac{2}{3} {(2 r)}^{3} . \end{matrix}

Ezt kellett bizonyítanunk.

Márki László (Budapest, Fazekas M. Gyak. Gimn.)

II. megoldás. A Cavalieri‐elv szerint két test térfogata egyenlő, ha bármely, egy adott síkkal párhuzamos sík a két testből egyenlő területű idomokat metsz ki. Ezt a következő kis módosítással fogjuk felhasználni: ha két testet bármely, egy adott síkkal párhuzamos síkkal metszve a kimetszett idomok területének aránya egy

k

szám, akkor a két test térfogatának aránya

k

.
Toljunk (írjunk) bele hengereink egyikébe egy

r

sugarú

G

gömböt; ez a hengert érinti, középpontja a henger tengelyén van. Az I. megoldásban használt

S'

sík

G

-ből

\sqrt[]{r^{2} - x^{2}}

sugarú

k

kört metsz ki, ennek területe

π (r^{2} - x^{2})

, ennélfogva

N

és

k

területének aránya

4 / π

, állandó. Így fenti elvünk szerint

K

és

G

térfogatainak aránya ugyancsak

4 / π

, tehát

\begin{matrix} V = \frac{4}{π} \cdot \frac{4 π}{3} r^{3} = \frac{2}{3} {(2 r)}^{3} . \end{matrix}

Elekes György (Budapest, Fazekas M. Gyak. Gimn.)