Kezdőlap


Feladat:	1398. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Baranyai Zs. , Deák J. , Domokos L. , Domokos Zsuzsanna , Elekes Gy. , Forgács P. , Malina J. , Márki László , Surányi László , Szász A. , Szemkeő Judit
Füzet:	1966/október, 52 - 54. oldal		PDF \| MathML
Témakör(ök):	Diszkusszió, Háromszögek szerkesztése, Feladat
Hivatkozás(ok):	Feladatok: 1965/május: 1398. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Csak azt kell bizonyítanunk, hogy az $A' B A B'$ törött vonal 3 egyenlő szakaszból áll.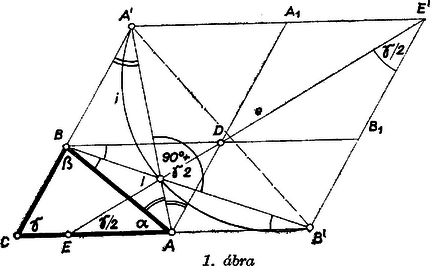

Egészítsük ki az

A' C B'

háromszöget

A' C B' E'

paralelogrammává (1. ábra). Az

e

egyenes átmegy

E'

-n és felezi az

A' E' B' = γ

szöget, mert

B' E' = C A' = p = q - (q - p) = C B' - C E = B' E

, az

E B' E'

háromszög egyenlő szárú,

B' E E'

szöge egyenlő a

B'

-nél levő

γ

külső szög felével, tehát

E E'

azonos

e

-vel. Így az 1399. feladatban bebizonyított tételt a

C B' E' A'

paralelogrammára,

E'

-ból induló

e

szögfelezőjének

I

pontjára és a

B' I

A' I

egyenessel kimetszett

A

B

pontra alkalmazva

B' A = A' B

.
Ha

A B < A' B = A B'

volna, akkor az

A A' B

és

A B' B

háromszögben

\begin{matrix} A A' B ∢ < A' A B ∢ és A B' B ∢ < A B B' ∢ . \end{matrix}

A háromszögek

A

-nál, ill.

B

-nél levő külső szögére

\begin{matrix} B A C ∢ & = A B' B ∢ + A B B' ∢ < 2 \cdot A B B' ∢ és \\ A B C ∢ & = A A' B ∢ + A' A B ∢ < 2 \cdot A' A B ∢ . \end{matrix}

Így egyrészt az

A B I

háromszögből, mivel

A I B ∢ = A' I B' ∢ = 90^{\circ} + γ / 2

\begin{matrix} A B B' ∢ + A' A B ∢ = 180^{\circ} - A I B ∢ = 90^{\circ} - γ / 2, \end{matrix}

másrészt az

A B C

háromszöget véve figyelembe

\begin{matrix} A B B' ∢ + A' A B ∢ > \frac{1}{2} (B A C ∢ + A B C ∢) = \frac{1}{2} (180^{\circ} - A C B ∢) = \\ = 90^{\circ} - γ / 2. \end{matrix}

A két összefüggés egymásnak ellentmond. ‐ Hasonlóan lehetetlenség következik az

A B > A' B

feltételből is, csak a ,,

<

'' és ,,

>

'' jel mindenütt felcserélődik. Így kell, hogy

A B = A' B = A B'

legyen, és ezt akartuk bizonyítani.

2. ábra

II. megoldás (az 1399. feladat felhasználása nélkül). Az előző megoldás záró meggondolásának eredményét így fogalmazhatjuk: ha

A B \leq A' B

és

A B \leq A B'

, akkor itt csak az egyenlőség jele állhat mindkét helyen, hasonlóan akkor is, ha mindkét helyen a ,,

\geq

'' jel áll. Meg kell még vizsgálnunk, nem állhat-e fenn

A' B \geq A B \geq A B'

vagy

A' B \leq A B \leq A B'

úgy, hogy ne mind a két helyen az egyenlőség jele legyen érvényes. Mérjük rá

B A'

-re a

B A^{*} = B A

és

A B'

-re az

A B^{*} = A B

távolságot (2. ábra). Első esetben

A A^{*}

B A A'

szögtartományban,

B B^{*}

A' B B'

szögtartományban van, tehát

I^{*}

metszéspontjuk az

A' B I

háromszögben van. Másrészt, ha nem áll mindkét helyen egyenlőség, akkor

C B^{*} - C A^{*} > C B' - C A' = C E

, tehát ezt mérve a

C B'

egyenesre egy

E

-n túli

E^{*}

pontba jutunk. Ebből húzva párhuzamost az

E I = e

egyenessel, azt

e

elválasztja az

A' B I

háromszögtől. Ez azonban nem lehet, mert a cikk elemzése szerint

I^{*}

e^{*}

-on van.
Hasonlóan a második esetben

A A^{*}

A' A B'

szögtartományban van,

B B^{*}

A B B'

tartományban, tehát

I^{*}

A I B'

háromszögben van, ha viszont nem áll mind a két helyen egyenlőség, akkor

C B^{*} - C A^{*} < C B' - C A' = C E

, s így

E^{*}

C E

szakaszra vagy a

C A'

szárra esik, s így

e

ismét elválasztja

e^{*}

-ot és

I^{*}

-ot, ami nem lehetséges. Kell tehát, hogy

A' B = B A = A B'

álljon.

Surányi László (Budapest, Fazekas M. Gyak. Gimn.)