Kezdőlap


Feladat:	1397. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Balogh K. , Domokos Zsuzsanna , Elekes Gy. , Korchmáros G. , Márki L. , Surányi L. , Székely G. , Szörényi M.
Füzet:	1966/április, 157 - 159. oldal		PDF \| MathML
Témakör(ök):	Magasságvonal, Magasságpont, Síkgeometriai számítások trigonometria nélkül háromszögekben, Feladat
Hivatkozás(ok):	Feladatok: 1965/május: 1397. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Ismeretes^{$^{*}$}, hogy minden háromszög $M$ magasságpontjának bármelyik oldalra való tükörképe a háromszög köré írt körön van. $M$ -et pl. a $B C$ oldalra való tükörképével összekötő egyenes merőleges az oldalra, ezért azonos az $A M$ magasság egyenesével, tehát a tükörkép a feladat előírása szerinti $A_{2}$ pont, és $A_{1} A_{2}$ és $M A_{1}$ egyenlők és egyirányúak.

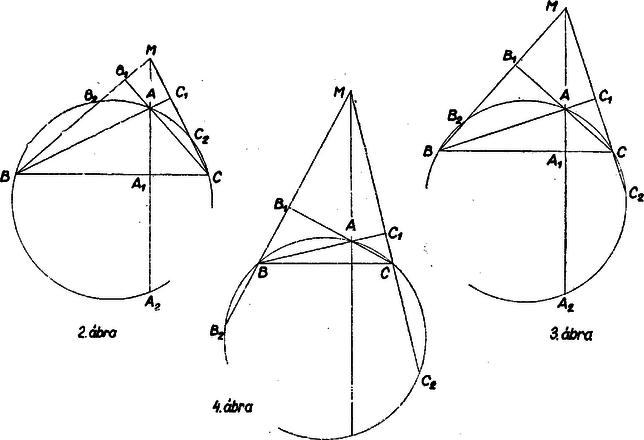
1. ábra

Hegyesszögű háromszög magasságpontja a háromszög belsejében van, így a pontok sorrendje a mondott magasságvonalon

A

M

A_{1}

A_{2}

(1. ábra), ezért (1) bal oldalának első tagja az alábbiak szerint alakítható:

\begin{matrix} \frac{A A_{2}}{A A_{1}} = \frac{A A_{1} + A_{1} A_{2}}{A A_{1}} = 1 + \frac{M A_{1}}{A A_{1}} = 1 + \frac{B C \cdot {M A}_{1}}{B C \cdot {A A}_{1}} = 1 + \frac{B C M}{B C A}, \end{matrix}

(2)

az utolsó törtben a

B C M

és

B C A

háromszög területeinek aránya áll, a területeket ugyanúgy jelöltük, mint magukat a háromszögeket.

(1) további két tagját hasonlóan alakítva a három tört nevezője közös, számlálóik összege a háromszög területe, így valóban

\begin{matrix} \frac{A A_{2}}{A A_{1}} + \frac{B B_{2}}{B B_{1}} + \frac{C C_{2}}{C C_{1}} = 3 + \frac{B C M + C A M + A B M}{A B C} = 3 + 1 = 4. \end{matrix}

II. Ha az

A

csúcsnál derékszög van, akkor ide esik a

B_{1}

C_{1}

magasságtalppont, egyszersmind

B_{2}

és

C_{2}

is, így (1) második és harmadik tagja

1

; másrészt a

B C

oldal ‐ mint átfogó ‐ a körülírt körnek átmérője, tehát

A_{2}

A

csúcs tükörképe,

A A_{2} = 2 A A_{1}

, tehát (1) első tagja

2

. Eszerint (1) változatlanul érvényes.

III. Ha

A

-nál tompaszög van (

2

‐

4

. ábrák), akkor (1) első tagja tetszés szerinti nagy értéket felvehet, ezért az állítás nem lehet igaz változatlanul. Megmutatjuk, hogy az állítás úgy marad helyes, ha alakján nem változtatunk, de a szakaszokat iránnyal együtt értjük, azaz ‐ mint a hegyesszögű háromszög esetében ‐ a hányadosokat akkor vesszük pozitívnak, ha a számlálóbeli szakasz egyirányú a nevezőbelivel; ha pedig azzal ellentétes irányú, akkor a hányados negatív. Ha viszont irányítást nem veszünk figyelembe, akkor tompaszögű háromszög esetében (1) bal oldaláról semmi határozottat nem állíthatunk.
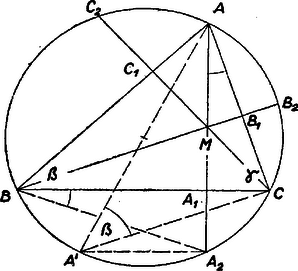
Feltevésünk szerint az

A_{1}

magasságtalppont a

B C

oldalszakaszon van, vagyis a körülírt kör belsejében, a

B_{1}

és

C_{1}

talppontok viszont a

C A

, ill.

B A

oldal

A

-n túli meghosszabbításán, a körön kívül.

M

is a körön kívül van,

A A_{1}

-nek a csúcson túli,

B B_{1}

-nek és

C C_{1}

-nek pedig a talpponton túli meghosszabbításán. Így a számláló az (1)-beli első hányadosban mindig egyirányú a nevezővel, a (2) átalakítás most is érvényes. A 2. és 3. hányadosban viszont az irányok lehetnek egyezők is, ellentétesek is, és lehet a számláló

0

is.
Ha

B B_{2}

egyező irányú

B B_{1}

-gyel, akkor a pontok sorrendje:

B

B_{2}

(a körön),

B_{1}

(a körön kívül),

M

(2. és 3. ábra); így

\begin{matrix} B B_{2} = B B_{1} - B_{2} B_{1} = B B_{1} - B_{1} M . \end{matrix}

Ellentétes irányítás esetén pedig

B_{2}

B

B_{1}

M

a sorrend (4. ábra), és

\begin{matrix} B B_{2} = - B_{2} B = - (B_{2} B_{1} - B B_{1}) = B B_{1} - B_{2} B_{1} = B B_{1} - B_{1} M, \end{matrix}

vagyis a két kifejezés alakra nézve ugyanaz. Hasonlóan adódik mindegyik lehetőség esetére

C C_{2} = C C_{1} - C_{1} M

. Ezek szerint

\begin{matrix} \frac{B B_{2}}{B B_{1}} = 1 - \frac{B_{1} M}{B B_{1}} = 1 - \frac{A C \cdot B_{1} M}{A C \cdot {B B}_{1}} = 1 - \frac{A C M}{A C B}, \frac{C C_{2}}{C C_{1}} = 1 - \frac{A B M}{A B C}, \end{matrix}

és (1) bal oldala így alakul

\begin{matrix} 3 + \frac{B C M - A C M - A B M}{A B C} . \end{matrix}

A

csúcs a

B C M

háromszög belsejében van, ezért a számláló egyenlő az

A B C

háromszög területével, és így a hányados

1

, a kifejezés értéke

4

. Ezt akartuk bizonyítani.

Domokos Zsuzsanna (Makó, József A. G. III. o. t.)

Megjegyzés. Az irányok (előjelek) figyelembevételének szükségességére más oldalról jövünk rá, ha az állítást trigonometriai és goniometriai úton bizonyítjuk. Egységnek véve a körülírt kör

A A'

átmérőjét, a szögek szokásos jelölésével az

A A_{1} C

és

A A' C

derékszögű háromszögekből (1. ábra):

\begin{matrix} A A_{1} = A C \cdot sin γ = A A' \cdot sin β sin γ = sin β sin γ, & (3) \\ mert A A' C ∢ = A B C ∢ = β . Másrészt az A A' A_{2} derékszögű háromszögben \\ A A' A_{2} ∢ = A B A_{2} ∢ = A B C ∢ + C B A_{2} ∢ = A B C ∢ + C A A_{2} ∢ = \\ = β + (90^{\circ} - γ) = 90^{\circ} - (γ - β), és így \\ A A_{2} = A A' \cdot sin A A' A_{2} ∢ = cos (γ - β) . & (4) \end{matrix}

Ezeket és az (1)-beli további szakaszokra adódó hasonló kifejezéseket (1) bal oldalába helyettesítve azonos átalakítások útján adódik az állítás helyessége.
Mármost (3) és a belőle a betűk ciklikus felcserélésével adódó

B B_{1} = sin γ sin α

C C_{1} = sin α sin β

kifejezések minden háromszögben pozitívok, viszont (4) és a

B B_{2} = cos (α - γ)

C C_{2} = cos (β - α) = cos (α - β)

jobb oldala lehet negatív is, amennyiben pl. a

α - γ

, ill.

α - β

tompaszög (3. és 4. ábra).

^{$^{*}$}Lásd pl. az 1272. feladat II. megoldásában, K.M.L. 29 (1964) 26. o.