Feladat: 1395. matematika feladat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Babai L. ,  Bajmóczy E. ,  Bárány I. ,  Darvas Gy. ,  Deák J. ,  Domokos L. ,  Fodor Magdolna ,  Füvesi I. ,  Gárdos Eszter ,  Gáspár A. ,  Horváth Rozália ,  Kiss Á. ,  Korchmáros G. ,  Lábadi A. ,  Lévai F. ,  Malina J. ,  Márki L. ,  Recski A. ,  Staub Klára ,  Steiner Gy. ,  Szántó O. ,  Szász A. ,  Szeidl L. ,  Székely G. ,  Szörényi M. ,  Tolnay-Knefély T. 
Füzet: 1966/február, 65 - 66. oldal  PDF  |  MathML 
Témakör(ök): Különleges függvények, Numerikus és grafikus módszerek, Feladat
Hivatkozás(ok):Feladatok: 1965/május: 1395. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. x-et megválasztva y-t logaritmussal számítjuk ki, pl. x=0,01 esetén lg  y=x  lg  x=0,01⋅(-2)=-0,02=0,9800-1, így y=0,955 (3 tizedes jegy pontosságú közelítő érték). Az ábrázoláshoz a következő értékpárokat használtuk fel:

xyxyxy0,01  0,955    0,35    0,693    0,9    0,909  0,03  0,900    0,4    0,693    1    1  0,05    0,861    0,5    0,707    1,1    1,110  0,1    0,794    0,6    0,736    1,2    1,245  0,2  0,725    0,7  0,779    1,3    1,406  0,3    0,697    0,8    0,837    1,4    1,6021,5    1,837  


Az értékpárokat ábrázoló pontokat egy rájuk illeszkedő sima görbével összekötöttük és ezt fogadtuk el függvényünk grafikonjának. A grafikon 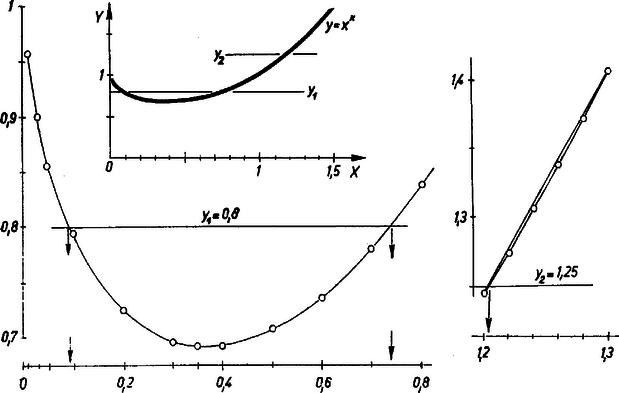x=0,01-tól kb. x=0,35-ig süllyed, eleinte gyorsabban, majd egyre lassabban, majd kb. 0,4-től 1,5-ig emelkedik, eleinte lassan, majd egyre gyorsabban.
 
 

II. Az adott egyenlet az y=xx ismeretlenre nézve másodfokú egyenlet:
y2-2,05y+1=0,
amiből y1=0,8, y2=1,25.
Az xx=0,8 egyenlet közelítő megoldására felhasználhatjuk grafikonunkat. Az y1=0,8 egyenes két pontban metszi a görbét: az első pont abszcisszája x=0,05 és x=0,1 közötti szám, jóval közelebb az utóbbihoz, a másodiké x=0,7 és x=0,8 közötti, az előbbihez valamivel közelebb.
Pontosabb közelítő értéket lineáris interpolációval keresünk. A grafikon süllyedése a 0,05 és 0,1 abszcisszájú pontok között 0,067, a 0,861 értéktől 0,8-ig pedig 0,061, az előbbinek kb. 9/10 része, ezért a két abszcissza közti növekedésnek is 9/10 részét véve azt várjuk, hogy a keresett gyök közel lesz x1=0,095-höz. Itt y értéke (lg  y=0,9029-1-ből), 0,7997≈0,8 további finomítás a négyjegyű függvénytáblázattal nem várható.
Hasonlóan a görbe 0,7 és 0,8 abszcisszájú pontjai között az emelkedés 0,058, mi pedig az előbbi ponttól y=0,8-ig 0,021 emelkedést keresünk, ami a teljes emelkedésnek közel 4/10 része (fölfelé kerekítünk, mert a görbe eleinte úgyis lassabban emelkedik), így a metszéspont abszcisszája közelítőleg x2=0,74. Ez megfelel, mert 0,740,74≈0,8002.
Az y2=1,25 egyenesnek a grafikonnal való metszéspontjából egy gyököt kapunk, ennek közelítő értéke hasonlóan x3=1,204.
Ezek szerint egyenletünknek 0,09 és 0,10 között van egy gyöke, 0,74 körül egy további, végül 1,20 és 1,21 között egy harmadik. (Meg lehet mutatni, hogy x>1,5 esetén nincs további gyök.)
 
Horváth Rozália (Celldömölk, Berzsenyi D. g. I. o. t.)