Kezdőlap


Feladat:	1391. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Babai L. , Balogh K. , Bárány I. , Deák J. , Domokos L. , Domokos Zsuzsanna , Forgács P. , Füvesi István , Gáspár A. , Herényi I. , Juhász F. , Kele A. , Kiss Á. , Lévai F. , Nagy Klára , Sükösd Cs. , Szalay M. , Szántó O. , Szemkeő Judit , Szőke P. , Szörényi Miklós , Takács J.
Füzet:	1967/január, 5 - 7. oldal		PDF \| MathML
Témakör(ök):	Egyenes körhengerek, Terület, felszín, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1965/április: 1391. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

a) Jelöljük a merőleges és ferde metszősíkot $S$ -sel és $S^{*}$ -gal,. (1. ábra), metszésvonalukat $e$ -vel, az $S$ -ben levő körmetszetet $k$ -val, középpontját $O$ -val. A leghosszabb és legrövidebb alkotó $k$ -nak az $e$ -től legtávolabbi $C$ és $e$ -hez legközelebbi $D$ pontjában $S$ -re emelt merőlegesnek $S^{*}$ -ig terjedő $C C^{*}$ , $D D^{*}$ szakasza, mert ha a pont az $S$ síkban mozog, ennek a merőleges szakasznak a hossza $e$ -től távolodva nő. $C D$ a $k$ kör $e$ -re merőleges átmérője.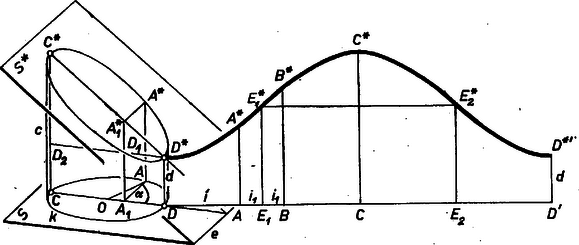

1. ábra

A palástot az előírt módon kiterítve

k

egy (

2 π r

-hosszúságú)

D D'

egyenesszakasszá terül ki. Kézenfekvő, és a követelménynek megfelel, ha a tetszés szerinti

A A^{*}

alkotót (a kiterített palást

D D'

-re merőleges metszetét) a

D D'

-n levő

A

végpontjának

D

-től mért

i

távolságával fejezzük ki. A síkba terítést végezhetjük úgy, hogy ez

k

D

-től pozitív irányban

A

-ig menő ívének a kiterítésével keletkezzék. Legyen a megfelelő

D O A ∢ = α (0 ≦ α ≦ 2 π)

. Ekkor

i = r α

.
Legyen

A

és

A^{*}

vetülete a

C D

, ill.

C^{*} D^{*}

szakaszon

A_{1}

, ill.

A_{1}^{*}

A_{1}

C

D

A_{1}^{*}

C^{*}

D^{*}

egy síkban vannak, a

C C^{*}

D D^{*}

párhuzamosok meghatározta síkban, továbbá

A_{1} A_{1}^{*} = A A^{*}

, mert

A A_{1} A_{1}^{*} A^{*}

paralelogramma (téglalap), ugyanis az

S

síkban

A A_{1} ⊥ C D ⊥ e

, így

A A_{1} ∥ e

, hasonlóan az

S^{*}

síkban

A^{*} A_{1}^{*} ⊥ C^{*} D^{*} ⊥ e

, így

A^{*} A_{1}^{*} ∥ e

, tehát

A A_{1} ∥ A^{*} A_{1}^{*}

. Az

A A^{*}

A_{1} A_{1}^{*}

oldalak is párhuzamosak, mert merőlegesek

S

-re, az utóbbi azért, mert az

A

A_{1}

A^{*}

és

A_{1}^{*}

-ot tartalmazó sík metszésvonala a

C

C^{*}

D

D^{*}

-ot tartalmazó síkkal, és ezek merőlegesek

S

-re, miután tartalmazzák az

S

-re merőleges

A A^{*}

ill.

C C^{*}

egyenest.
Messe a

D^{*}

-ból

C D

-vel párhuzamosan húzott egyenes

A_{1} A_{1}^{*}

-ot

D_{1}

-ben,

C C^{*}

-ot

D_{2}

-ben. A

C^{*} D^{*} D_{2}

és

A_{1}^{*} D^{*} D_{1}

hasonló háromszögekből

\begin{matrix} \frac{D_{1} A_{1}^{*}}{D_{2} C^{*}} = \frac{D^{*} D_{1}}{D^{*} D_{2}} = \frac{r - O A_{1}}{2 r} = \frac{1 - cos α}{2} . \end{matrix}

(Eredményünk akkor is helyes, ha

D^{*} D_{1} > r

), másrészt

\begin{matrix} \frac{D_{1} A_{1}^{*}}{D_{2} C^{*}} = \frac{A_{1} A_{1}^{*} - d}{c - d} = \frac{A A^{*} - d}{c - d} . \end{matrix}

Innen a keresett összefüggés,

α

-t

i

-vel fejezve ki

\begin{matrix} A A^{*} = = \frac{c - d}{2} (1 - cos \frac{i}{r}) + d = \frac{c + d}{2} - \frac{c - d}{2} cos \frac{i}{r} (0 ≦ i ≦ 2 π r) . \end{matrix}

Eszerint a palást görbe határvonala a

z = cos i

függvény képéből áll elő úgy, hogy ezt az

i

-tengely irányában

r

-szeresére, a

z

-tengely irányában

- (c - d) / 2

-szeresére nyújtjuk (vagyis

(c - d) / 2

-szeresére nyújtjuk és tükrözzük az

i

-tengelyre), végül a

z

-tengely irányában

(c + d) / 2

szakasszal eltoljuk.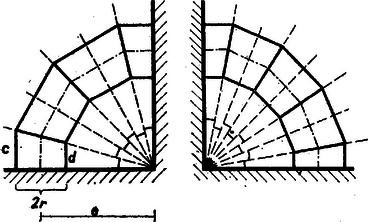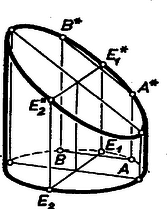

2. ábra

3. ábra

A hengerpalást felszínének meghatározásához belátjuk a következőt. Legyen

E_{1} E_{2}

k

kör

e

-vel párhuzamos átmérője (3. ábra),

E_{1} E_{1}^{*}

E_{2} E_{2}^{*}

a végpontjain átmenő alkotók

S^{*}

-ig terjedő szakaszai

(E_{1} E_{1}^{*} = E_{2} E_{2}^{*})

. Ekkor a csődarabot

E_{1}^{*} E_{2}^{*}

-on át

S

-sel párhuzamos síkkal elvágva, és a sík feletti részt

E_{1}^{*} E_{2}^{*}

körül

180^{\circ}

-kal elforgatva a csődarabot egyenes körhenger-palásttá lehet átalakítani.
Valóban, ha

A

és

B

k

E_{1} E_{2}

-re szimmetrikus pontjai, és

A A^{*}

B B^{*}

a rajtuk átmenő alkotószakaszok, akkor

A^{*}

és

B^{*}

is egymás tükörképei

E_{1}^{*} E_{2}^{*}

-ra, tehát összekötő szakaszuk felezőpontja

E_{1}^{*} E_{2}^{*}

-on van. Mivel ez az egyenes párhuzamos

e

-vel, s így az

S

síkkal is, így

A A^{*} + B B^{*} = 2 E_{1} E_{1}^{*}

. Így az említett elmetszés és átforgatás után valóban minden alkotószakasz egyenlő hosszúvá válik. Mivel

C

és

D

E_{1} E_{2}

-re szimmetrikus, így a keletkező egyenes körhenger magassága

\begin{matrix} \frac{1}{2} (C C^{*} + D D^{*}) = \frac{c + d}{2}, \end{matrix}

és a hengerpalást felszíne

π r (c + d)

.
b) A 2. ábra szerinti könyökcsövek 6, ill. 8 olyan egybevágó darabra bonthatók fel, amilyeneknek a felszínét fent számítottuk. A jelölt szögek nagysága

β = 90^{\circ} / 6 = 15^{\circ}

, ill.

γ = 11, 25^{\circ}

. A fenti képletben

c + d

a csődarab trapéz alakú vetülete középvonalának 2-szerese, és az első középvonal

e

-vel derékszögű háromszöget alkot, tehát a könyökcsövek felszíne:

\begin{matrix} 12 π r e tg 15^{\circ} \approx 10, 1 r e, ill. \end{matrix}

\begin{matrix} 16 π r e tg 11, 25^{\circ} \approx 10, 0 r e . \end{matrix}

Szörényi Miklós (Pécs, Széchenyi I. G.)

Füvesi István (Hódmezővásárhely, Bethlen G. G.)

Megjegyzés. Meghatározható a palást felszíne azon keresztül is, hogy ha a kiterített palástot a

D D'

határának

E_{1}

első és

E_{2}

harmadik negyedelő pontjában emelt merőlegesek

E_{1}^{*}, E_{2}^{*}

végpontjain átmenő egyenessel elmetsszük, az egyenes feletti darabot a

C C^{*}

egyenessel kettévágjuk, és a részeket

E_{1}^{*}

, ill.

E_{2}^{*}

körül

180^{\circ}

-kal

D E_{1}

, ill.

E_{2} D'

szakasz fölé forgatjuk. Ekkor téglalapot kapunk. Valóban, pl. két az

E_{1}

-re szimmetrikus

A

és

B

pontban húzott ordináta összege

\begin{matrix} \frac{c + d}{2} - \frac{c - d}{2} cos \frac{π r / 2 - i_{1}}{r} + \frac{c + d}{2} - \frac{c - d}{2} cos \frac{π r / 2 + i_{1}}{r} = \end{matrix}

\begin{matrix} = (c + d) - \frac{c - d}{2} [cos (\frac{π}{2} - \frac{i_{1}}{r}) + cos (\frac{π}{2} + \frac{i_{1}}{r})] = c + d . \end{matrix}

(0 ≦ i_{1} < \frac{π r}{2})