Kezdőlap


Feladat:	1390. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bárány I. , Deák J. , Domokos L. , Domokos Zsuzsanna , Gáspár A. , Herényi I. , Kovács M. , Lamm P. , Nagy Klára , Óhegyi E. , Surányi L. , Sükösd Cs. , Szalay M. , Szántó O. , Szeidl Lászó , Szörényi M.
Füzet:	1966/április, 155 - 157. oldal		PDF \| MathML
Témakör(ök):	Súlyvonal, Szinusztétel alkalmazása, Koszinusztétel alkalmazása, Feladat
Hivatkozás(ok):	Feladatok: 1965/április: 1390. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Betűzzük az $A B C$ háromszöget úgy, hogy $B C \geq A C$ , és legyen adott $B C + C A = a + b = e$ (ill. $a - b = f$ , itt természetesen csak az $a > b$ , $f > 0$ esettel foglalkozunk, különben csak egyenlő szárú háromszöget kell megoldani), $A C B ∢ = γ$ , $C C_{1} = s_{c}$ , ahol $C_{1}$ az $A B$ oldal felezőpontja, legyen továbbá $C$ tükörképe $C_{1}$ -re $D$ . Így $A C B D$ paralelogramma, és az $A C D$ háromszögből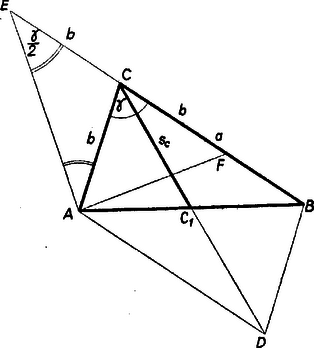

\begin{matrix} 4 s_{c}^{2} = & a^{2} + b^{2} - 2 a b cos (180^{\circ} - γ) = {(a - b)}^{2} - 2 a b (1 - cos γ), ill. \\ = & {(a - b)}^{2} + 2 a b (1 + cos γ), innen \\ a b = \frac{e^{2} - 4 s_{c}^{2}}{2 (1 - cos γ)} = g, ill. - a b = \frac{f^{2} - 4 s_{c}^{2}}{2 (1 + cos γ)} = h, \end{matrix}

ennélfogva

a

és

b

(ill.

- b

) a következő másodfokú egyenlet gyökei:

\begin{matrix} u^{2} - e u + g = 0, \end{matrix}

ill.

\begin{matrix} v^{2} - f v + h = 0. \end{matrix}

Innen

\begin{matrix} a = \frac{e}{2} + \frac{\sqrt[]{4 s_{c}^{2} - e^{2} cos^{2} (γ / 2)}}{2 sin γ / 2}, \end{matrix}

(1)

ill.

\begin{matrix} a = \frac{f}{2} + \frac{\sqrt[]{4 s_{c}^{2} - f^{2} sin^{2} (γ / 2)}}{2 cos γ / 2}, \end{matrix}

(2)

amivel

b

is meg van határozva.
Az

A B C

háromszögből

\begin{matrix} c^{2} = a^{2} + b^{2} - 2 a b cos γ = {(a + b)}^{2} - 2 a b (1 + cos γ) = e^{2} - \\ - (e^{2} - 4 s_{c}^{2}) \cdot \frac{1 + cos γ}{1 - cos γ} = e^{2} (1 - {cotg}^{2} \frac{γ}{2}) + 4 s_{c}^{2} {cotg}^{2} \frac{γ}{2}, \end{matrix}

ill. hasonlóan

\begin{matrix} c^{2} = {(a - b)}^{2} + 2 a b (1 - cos γ) = f^{2} - (f^{2} - 4 s_{c}^{2}) \cdot \frac{1 - cos γ}{1 + cos γ} = \\ = f^{2} (1 - {tg}^{2} \frac{γ}{2}) + 4 s_{c}^{2} {tg}^{2} \frac{γ}{2} . \end{matrix}

Mérjük rá a

b

oldalt

C

-től a

B C

oldal meghosszabbítására, ill.

B

felé, és legyen a végpont

E

, ill.

F

. Így

C A E

és

C A F

egyenlő szárú háromszögek,

A F

merőleges

A E

-re,

B E = e

B F = f

, a külső szög tétele alapján

C E A ∢ = B E A ∢ = γ / 2

B F A ∢ = 90^{\circ} + γ / 2

, továbbá

B A E ∢ = α + γ / 2 = 90^{\circ} + (α - β) / 2

B A F ∢ = (α - β) / 2

, ezért az

A B E

A B F

háromszögből a színusz-tétel alapján

\begin{matrix} sin B A E ∢ = cos \frac{α - β}{2} = \frac{B E}{B A} \cdot sin A E B ∢ = \frac{e}{c} sin \frac{γ}{2}, ill. \\ sin B A F ∢ = sin \frac{α - β}{2} = \frac{f}{c} sin B F A ∢ = \frac{f}{c} cos \frac{γ}{2}, \end{matrix}

ennélfogva

α

-t és

β

-t a különbségükre és az összegükre fennálló egyenletrendszerből kapjuk (

α - β

egyértelműen meghatározott, mert a fele hegyesszög).
A feladat megoldhatóságának első feltétele, hogy az

A C D

háromszög létezzék:

\begin{matrix} C A + A D > C D, azaz e > 2 s_{c}, ill. f < 2 s_{c} . \end{matrix}

f

az adott, további feltétel nincs is, mert így (2)-ben a diszkrimináns pozitív. Amennyiben

e

adott, akkor

a

valós, ha

\begin{matrix} 2 s_{c} \geq e cos \frac{γ}{2}, a fentivel összefoglalva e cos \frac{γ}{2} \leq 2 s_{c} < e . \end{matrix}

További feltétel nincs,

c

valós, mert

a

b

és

γ

bármely értékrendszeréhez tartozik

c

Szeidl László (Budapest, Apáczai Csere J. gyak. g. III. o. t.)