Kezdőlap


Feladat:	1388. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Arányi P. , Bárány I. , Darvas Gy. , Deák J. , Domokos L. , Domokos Zsuzsanna , Elekes Gy. , Fodor Magdolna , Gellért J. , Herényi I. , Hoffer Anna , Höss Rozália , Jakab M. , Juhász F. , Kalmár I. , Karsai Kornélia , Kiss Árpád , Kósa M. , Külvári I. , Lábadi A. , Lamm P. , Lévai F. , Márki L. , Nagy Klára , Sarkadi Nagy I. , Steiner Gy. , Surányi L. , Sükösd Cs. , Szabó I. , Szalay M. , Szász A. , Szeidl L. , Szőke P. , Szörényi M. , Tóth Teréz , Vermes D.
Füzet:	1966/április, 152 - 154. oldal		PDF \| MathML
Témakör(ök):	Harmadfokú (és arra visszavezethető) egyenletek, Kör egyenlete, Parabola egyenlete, Feladat
Hivatkozás(ok):	Feladatok: 1965/április: 1388. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az előírt kör $K$ középpontjának koordinátái $K (p, q)$ . Ezek ismerete elegendő a kör megrajzolásához, mert a körnek át kell mennie az $O$ origón, hiszen az $x = 0$ , $y = 0$ értékpár kielégíti az egyenletet.
A parabolának és a körnek legfeljebb $4$ közös pontja lehet. Ugyanis a két egyenletből $y$ -t kiküszöbölve $4$ -edfokú egyenletet kapunk:

\begin{matrix} k^{2} x^{4} + (1 - 2 k q) x^{2} - 2 p x = 0, \end{matrix}

(1)

így legfeljebb

4

valós szám szerepelhet közös pont abszcisszájaként, és a parabolának minden abszcisszán csak egy pontja van. Egy közös pontjuk az origó, további közös pontjaik abszcisszái azt az egyenletet elégítik ki, amelyet (1)-ből az ismert

x = 0

gyökhöz tartozó

x

gyöktényező leválasztásával kapunk:

\begin{matrix} k^{2} x^{3} + (1 - 2 k q) x - 2 p = 0. \end{matrix}

Itt

k \neq 0

‐ különben parabola helyett az

y = 0

egyenessel állnánk szemben ‐, ezért az egyenlet ekvivalens az alábbival:

\begin{matrix} x^{3} + \frac{1 - 2 k q}{k^{2}} \cdot x - \frac{2 p}{k^{2}} = 0. \end{matrix}

(2)

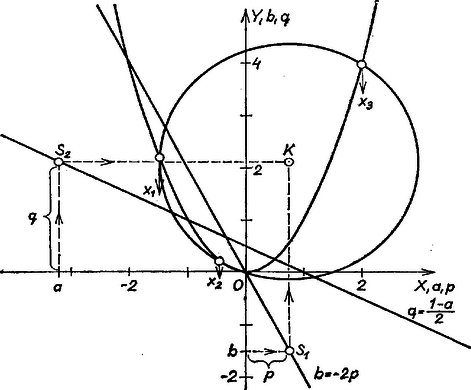A parabolának és a körnek az origótól különböző metszéspontjaihoz tartozó abszcisszák adják meg az

\begin{matrix} x^{3} + a x + b = 0 \end{matrix}

(3)

egyenlet gyökeit ‐ azaz minden valós gyökét ‐, ha (2) ekvivalens (3)-mal, vagyis ha további két együtthatójuk rendre egyenlő:

\begin{matrix} \frac{1 - 2 k q}{k^{2}} & = a, - \frac{2 p}{k^{2}} = b, és innen \\ p & = - \frac{k^{2}}{2} \cdot b, q = \frac{1}{2 k} - \frac{k}{2} \cdot a . & (4) \end{matrix}

Ezek szerint a (3) egyenlet valós gyökeit leolvashatjuk, mint az adott

y = k x^{2}

parabola és a (4) kifejezésekkel meghatározott

K

(p, q)

középpontú,

K O

sugarú kör közös pontjainak abszisszáit. Pl.

k = 1

-et választva a

\begin{matrix} K (- \frac{b}{2}, \frac{1 - a}{2}) \end{matrix}

középpont körüli,

O

-n átmenő körrel kell metszenünk a normálparabolát.
Az ábrán a

4 x^{3} - 13 x - 6 = 0

egyenlet megoldása látható, itt

p = 3 / 4

q = 17 / 8

, továbbá

x_{1} = - 3 / 2

x_{2} = - 1 / 2

x_{3} = 2

Recski András (Budapest, Bolyai J. g. III. o. t.)

Megjegyzés. Kézenfekvő, hogy a harmadfokú egyenlet grafikus megoldásában a

p, q

koordinátákat is grafikusan állítsuk elő. Erre valók (továbbra is

k = 1

esetében) az ábra segédegyenesei, melyeknek egyenlete

\begin{matrix} x = - \frac{y}{2}, ill. y = \frac{1 - x}{2} . \end{matrix}

Az elsőnek

y = b

ordinátájú

S_{1}

pontjához

x = - b / 2 = p

abszcissza tartozik, tehát

K = S_{1}

segédponton átmenő, az

Y

-tengellyel párhuzamos egyenesen lesz. A második segédegyenes

x = a

abszcisszájú

S_{2}

pontjához tartozó ordináta

y = (1 - a) / 2 = q

, tehát

K

-t a legutóbbi egyenesből az

S_{2}

-n átmenő, az

X

-tengellyel párhuzamos egyenes metszi ki.