Kezdőlap


Feladat:	1383. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Almási L. , Bárány I. , Baranyai Zs. , Dabóczy Á. , Deák J. , Domokos L. , Eff L. , Forgács P. , Füvesi I. , Gáspár A. , Kiss Á. , Lévai F. , Malina J. , Márki L. , Nagy Zsuzsa , Steiner Gy. , Surányi L. , Szántó O. , Székely G. , Szemkeő J. , Szörényi Miklós , Telegdy L.
Füzet:	1966/január, 20 - 21. oldal		PDF \| MathML
Témakör(ök):	Két pont távolsága, szakasz hosszúsága, Parabola egyenlete, Kúpszeletek érintői, Osztópontok koordinátái, Feladat
Hivatkozás(ok):	Feladatok: 1965/március: 1383. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A szóban forgó szelő végpontjai abszcisszáinak különbsége 1, ezért iránytangense egyenlő az ordináták különbségével, $2 n + 1$ -gyel. Így a szelő egyenlete

\begin{matrix} y = (2 n + 1) (x - n) + n^{2} = (2 n + 1) x - (n^{2} + n) . \end{matrix}

(1)

Tudjuk, hogy az

y = x^{2}

parabola bármely pontbeli érintőjének iránytényezője 2-szer akkora, mint az érintési pont abszcisszája, így az adott szelővel párhuzamos érintő érintési pontjának koordinátái:

\begin{matrix} T (n + \frac{1}{2}, {(n + \frac{1}{2})}^{2}) = T (n + \frac{1}{2}, n^{2} + n + \frac{1}{4}) . \end{matrix}

A kérdéses távolságot

T

-nek az (1) egyenesen levő

U

vetületétől való távolsága adja meg, ami az ismert képlet alkalmazásával a

\begin{matrix} d = T U = \frac{(n^{2} + n + 1 / 4) - (2 n + 1) (n + 1 / 2) + (n^{2} + n)}{\sqrt[]{{(2 n + 1)}^{2} + 1}} = \\ = \frac{- 1}{4 \sqrt[]{4 n^{2} + 4 n + 2}} \end{matrix}

kifejezés abszolút értéke.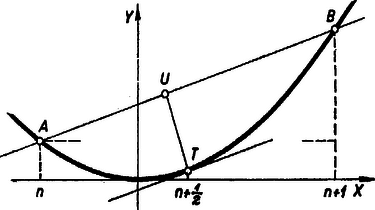

A kérdéses

k

arány megállapításához elég

U

egyik koordinátáját kiszámítanunk, ugyanis egy szakasz részeinek aránya egyenlő vetülete megfelelő részeinek arányával, és így

\begin{matrix} \frac{A U}{U B} = k = \frac{x_{U} - x_{A}}{x_{B} - x_{U}} = \frac{y_{U} - y_{A}}{y_{B} - y_{U}} \end{matrix}

(2)

(ahol

A

és

B

a szakasz végpontjai).
A

T U

egyenes egyenlete

\begin{matrix} y = - \frac{1}{2 n + 1} (x - n - \frac{1}{2}) + n^{2} + n + \frac{1}{4} . \end{matrix}

(3)

(1)-ből és (3)-ból

y

kiküszöbölésével

\begin{matrix} x_{U} = \frac{4 n^{3} + 6 n^{2} + 7 n / 2 + 3 / 4}{4 n^{2} + 4 n + 2} = n + \frac{1}{2} - \frac{2 n + 1}{4 (4 n^{2} + 4 n + 2)}, \end{matrix}

és így

x_{A} = n

x_{B} = n + 1

és (2) alapján

\begin{matrix} k = \frac{\frac{1}{2} - \frac{2 n + 1}{4 (4 n^{2} + 4 n + 2)}}{\frac{1}{2} + \frac{2 n + 1}{4 (4 n^{2} + 4 n + 2)}} = \frac{8 n^{2} + 6 n + 3}{8 n^{2} + 10 n + 5} = \\ = 1 - \frac{4 n + 2}{8 n^{2} + 10 n + 5} = 1 - \frac{1}{2 n + \frac{3}{2} + \frac{1}{2 n + 1}} . \end{matrix}

n

abszolút értékének növekedésével a második tag abszolút értéke tetszés szerinti kicsire lecsökken, vagyis az arány egyre kevesebbel tér el 1-től.
Az utolsó előtti alak 2. tagjának nevezője minden

n

-re pozitív, számlálójának előjele az

n = - 1 / 2

értéken való áthaladáskor változik, így

n < - 1 / 2

esetén

k > 1

n > - 1 / 2

esetén

k < 1

, végül

n = - 1 / 2

esetén

k = 1

. Könnyű belátni, hogy

n = - 1 / 2

esetén

U

a parabola fókuszába esik.

Szörényi Miklós (Pécs, Széchenyi I. Gimn., IV. o. t.)