Feladat:	1381. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bozóky Szeszich Ádám ,  Hoffer Anna
Füzet:	1966/február, 61 - 63. oldal		PDF  |  MathML
Témakör(ök):	Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1965/március: 1381. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.     1. ábra   I. megoldás. Legyen az $ABC$ háromszögben $BAC\sphericalangle =\alpha$, $ABC\sphericalangle ={90}^{\circ }$ és $AB=1$, továbbá a $BC$ befogó $C$-n túli meghosszabbításának $D$ pontjára $CAD\sphericalangle =\beta$ és így $BAD\sphericalangle =\alpha +\beta$, hegyesszög. Messe az $AC$-re $C$-ben állított merőleges $AD$-t $E$-ben és az $E$-n át $BD$-re állított merőleges $BD$-t $F$-ben (1. ábra). Ekkor $FCE\spheri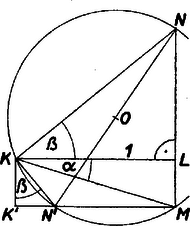calangle =\alpha$ és $FED\sphericalangle =\alpha +\beta$, továbbá $\begin{array}{c}{\displaystyle BC=\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\alpha \mathrm{,}AC=\frac{1}{\text{cos}\alpha }\mathrm{,}CE=\frac{\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\beta }{\text{cos}\alpha }\mathrm{,}CF=\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\beta \mathrm{,}}\end{array}$ ${\displaystyle \begin{array}{cc}\hfill {\displaystyle }& {\displaystyle EF=\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\beta \text{<span style="font-weight: normal;font-style: normal;">tg</span>}\alpha \mathrm{,}}\hfill \\ \hfill {\displaystyle }& {\displaystyle DF=\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\alpha \text{<span style="font-weight: normal;font-style: normal;">tg</span>}\beta \text{<span style="font-weight: normal;font-style: normal;">tg</span>}\left(\alpha +\beta \right);}\hfill \end{array}}$ másrészt $\begin{array}{c}{\displaystyle BC+CF+FD=BD=\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\left(\alpha +\beta \right)\mathrm{.}}\end{array}$ Az előbbieket ide behelyettesítve, végül $\alpha +\beta$ tangensét kifejezve ${\displaystyle \begin{array}{c}\hfill {\displaystyle \text{<span style="font-weight: normal;font-style: normal;">tg</span>}\alpha +\text{<span style="font-weight: normal;font-style: normal;">tg </span>}\beta +\text{<span style="font-weight: normal;font-style: normal;">tg </span>}\alpha \text{<span style="font-weight: normal;font-style: normal;">tg </span>}\beta \text{<span style="font-weight: normal;font-style: normal;">tg </span>}\left(\alpha +\beta \right)=\text{<span style="font-weight: normal;font-style: normal;">tg </span>}\left(\alpha +\beta \right)\mathrm{,}}\hfill \\ \hfill {\displaystyle \text{<span style="font-weight: normal;font-style: normal;">tg </span>}\left(\alpha +\beta \right)=\frac{\text{<span style="font-weight: normal;font-style: normal;">tg </span>}\alpha +\text{<span style="font-weight: normal;font-style: normal;"> tg </span>}\beta }{1-\text{<span style="font-weight: normal;font-style: normal;">tg </span>}\alpha \text{<span style="font-weight: normal;font-style: normal;"> tg </span>}\beta }\mathrm{.}}\hfill & \text{(<mn>1</mn>)}\end{array}}$   Hoffer Anna (Budapest, Hámán K. g. IV. o. t.)     2. ábra   II. megoldás. Legyen a $KLM$ és $KLN$ háromszögekben $L$-nél derékszög úgy, hogy $M$ és $N$ az $L$ két oldalán helyezkednek el (2. ábra), továbbá $KL=1$, és az $LKM\sphericalangle =\alpha$, $LKN\sphericalangle =\beta$ hegyesszögek összege is hegyesszög. Ekkor a $KMN$ háromszög köré írt kör $O$ középpontja $MN$-nek azon a partján van, mint $K$, ugyanígy az $NN\text{'}$ átmérő $N\text{'}$ végpontja is, így $NN\text{'}M\sphericalangle =\alpha +\beta$, $NMN\text{'}\sphericalangle =NKN\text{'}\sphericalangle ={90}^{\circ }$, $N\text{'}M$ párhuzamos $KL$-lel. Legyen végül $K$ vetülete $N\text{'}M$-re $K\text{'}$, Így $K\text{'}KN\text{'}\sphericalangle =\beta$, mert szárai merőlegesek $KL$-re, ill. $KN$-re. Ekkor $\begin{array}{c}{\displaystyle \text{<span style="font-weight: normal;font-style: normal;">tg</span>}\left(\alpha +\beta \right)=\text{<span style="font-weight: normal;font-style: normal;">tg</span>}NN\text{'}M\sphericalangle =\frac{MN}{MN\text{'}}=\frac{ML+LN}{MK\text{'}-N\text{'}K\text{'}}=\frac{\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\alpha +\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\beta }{1-N\text{'}K\text{'}}\mathrm{,}}\end{array}$ mert $KK\text{'}ML$ téglalap. A nevező második tagja $N\text{'}K\text{'}=KK\text{'}\text{<span style="font-weight: normal;font-style: normal;"> tg</span>}\beta =LM\text{<span style="font-weight: normal;font-style: normal;">tg </span>}\beta =\text{<span style="font-weight: normal;font-style: normal;">tg </span>}\alpha \text{<span style="font-weight: normal;font-style: normal;"> tg </span>}\beta$, így ismét $\begin{array}{c}{\displaystyle \text{<span style="font-weight: normal;font-style: normal;">tg </span>}\left(\alpha +\beta \right)=\frac{\text{<span style="font-weight: normal;font-style: normal;">tg </span>}\alpha +\text{<span style="font-weight: normal;font-style: normal;">tg </span>}\beta }{1-\text{<span style="font-weight: normal;font-style: normal;">tg </span>}\alpha \text{<span style="font-weight: normal;font-style: normal;"> tg </span>}\beta }\mathrm{.}}\end{array}$ Bozóky Szeszich Ádám (Budapest, Berzsenyi D. g. I. o. t.)     3. ábra   Megjegyzés. A bizonyítás kiterjeszthető arra az esetre is, ha $\alpha +\beta$ tompaszög (3. ábra): ${\displaystyle \begin{array}{c}\hfill {\displaystyle \text{<span style="font-weight: normal;font-style: normal;">tg</span>}\left(\alpha +\beta \right)=-\text{<span style="font-weight: normal;font-style: normal;">tg</span>}NN\text{'}M\sphericalangle =-\frac{MN}{MN\text{'}}=-\frac{ML+LN}{N\text{'}K\text{'}-MK\text{'}}=}\hfill \\ \hfill {\displaystyle \frac{\text{<span style="font-weight: normal;font-style: normal;">tg </span>}\alpha +\text{<span style="font-weight: normal;font-style: normal;">tg </span>}\beta }{1-N\text{'}K\text{'}}\mathrm{.}}\hfill \end{array}}$ III. megoldás. Messe az $\alpha +\beta$ szög $O$ csúcsa körül írt, egységnyi sugarú kör $\alpha$ és $\beta$ közös szárát $P$-ben, a $P$-beli érintő $\beta$ másik szárát $Q$-ban, és a $Q$-ból $\alpha$ másik szárára bocsátott merőleges ezt a szárt $R$-ben (a metszés létrejön, mert $\alpha +\beta$ hegyesszög), a közös szárt $S$-ben (4. ábra). Ekkor 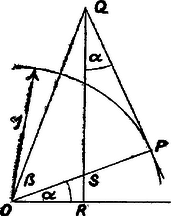$PQS\sphericalangle =\alpha$, $PQ=\text{<span style="font-weight: normal;font-style: normal;">tg </span>}\beta$, továbbá $\begin{array}{c}{\displaystyle \text{<span style="font-weight: normal;font-style: normal;">tg </span>}\left(\alpha +\beta \right)=\frac{RQ}{OR}=\frac{RS+SQ}{OR}=\text{<span style="font-weight: normal;font-style: normal;">tg </span>}\alpha +\frac{SQ}{OR}\mathrm{.}}\end{array}$ (2)     4. ábra   Itt $SQ=SP/\text{sin}\alpha$, $SP=QP\text{<span style="font-weight: normal;font-style: normal;"> tg </span>}\alpha =\text{<span style="font-weight: normal;font-style: normal;"> tg </span>}\beta \text{<span style="font-weight: normal;font-style: normal;"> tg </span>}\alpha$, másrészt $OR=OS\text{cos}\alpha$, és $OS=OP-SP=1-\text{<span style="font-weight: normal;font-style: normal;">tg </span>}\alpha \text{<span style="font-weight: normal;font-style: normal;"> tg </span>}\beta$. Ezért (2) második tagja ${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{\frac{\text{<span style="font-weight: normal;font-style: normal;">tg </span>}\alpha \text{<span style="font-weight: normal;font-style: normal;"> tg </span>}\beta }{\text{sin}\alpha }}{\left(1-\text{<span style="font-weight: normal;font-style: normal;">tg </span>}\alpha \text{<span style="font-weight: normal;font-style: normal;"> tg </span>}\beta \right)\text{cos}\alpha }=}\hfill \\ \hfill {\displaystyle \frac{\text{<span style="font-weight: normal;font-style: normal;">tg </span>}\beta }{1-\text{<span style="font-weight: normal;font-style: normal;">tg </span>}\alpha \text{<span style="font-weight: normal;font-style: normal;"> tg </span>}\beta }\cdot \frac{\text{sin}{}^2\alpha +\text{cos}{}^2\alpha }{\text{cos}{}^2\alpha }=\frac{\left({\text{<span style="font-weight: normal;font-style: normal;">tg</span>}}^2\alpha +1\right)\text{<span style="font-weight: normal;font-style: normal;"> tg </span>}\beta }{1-\text{<span style="font-weight: normal;font-style: normal;">tg </span>}\alpha \text{<span style="font-weight: normal;font-style: normal;"> tg </span>}\beta }\mathrm{,}}\hfill \end{array}}$ és így közös nevezőre hozással ismét (1) adódik.